Bočno izvijanje i izvijanje pri torziji

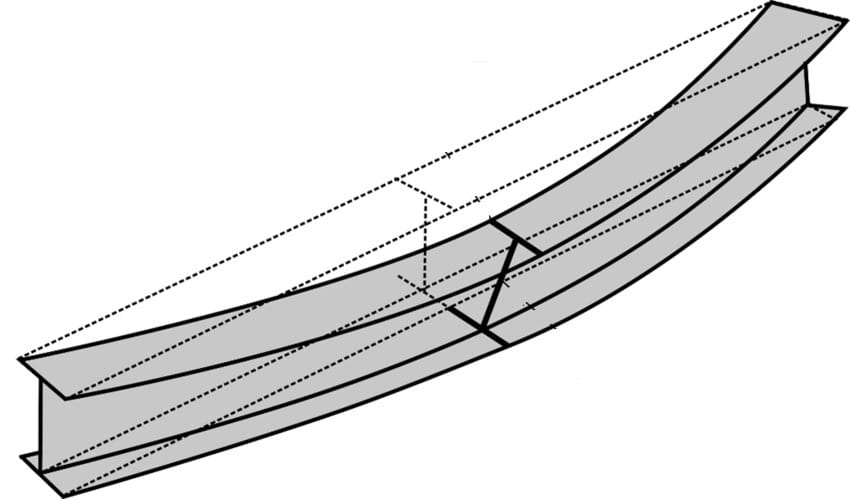
Za izvijanje pri savijanju štap je pri promeni ravnoteže savijen u jednoj glavnoj ravni.

Ali ima i takvih slučajeva stabilnosti kod kojih štap, odn. greda pri promeni ravnoteže bivaju ne samo savijeni već i uvijeni (sl. 60a). Kod nosača ova pojava zove se bočno izvijanje, kod pritisnutih štapova, koji su prilikom izvijanja izloženi takođe torziji, govori se o izvijanju pri torziji.

Za obe pojave je od odlučujućeg značaja veličina krutosti protiv torzije C, odn. otpor krivljenju C*. Na promenu ravnoteže spojenu sa torzijom može stoga u prvom redu da se utiče merama koje povećavaju krutost protiv uvijanja (odgovarajući oblik preseka, poprečni okviri, bočno podupiranje itd.). S druge strane, štapovi u obliku trake sa otvorenim presekom naročito su osetljivi na izvijanje pri torziji.

 

Diferencijalna jednačina za bočno izvijanje

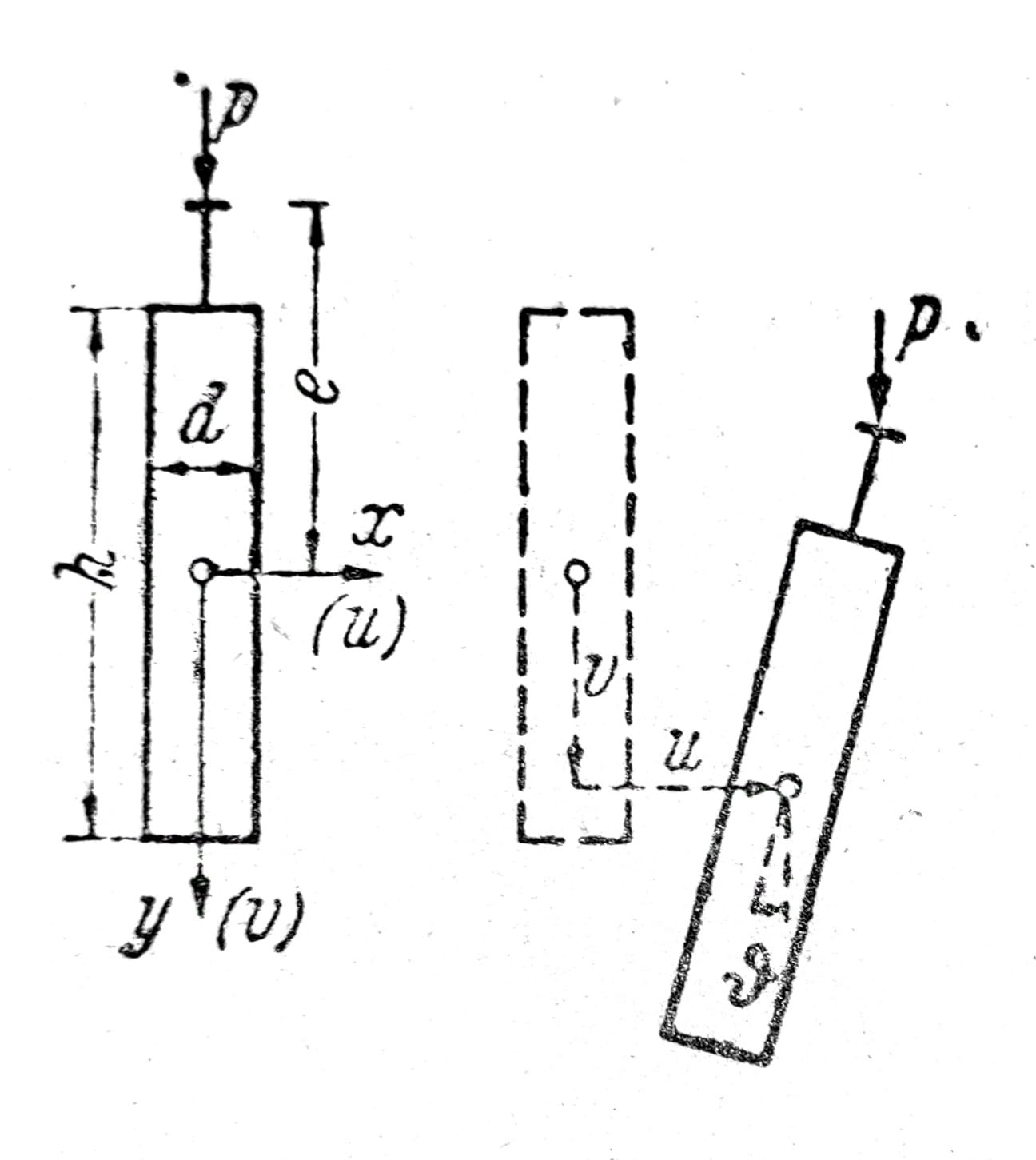
Sl. 1a

Neka prava greda ima konstantne momente inercije vrlo nejednake veličine I_x >> I_y. Opterećenje leži u y-z-ravni tako da će greda biti savijena u ovoj glavnoj ravni (u=ϑ=0). Iskustvo kao i teorija pokazuju da je ovaj ravnotežni položaj prvo stabilan, ali da za veća opterećenja postaje labilan. Ovaj drugi ravnotežni položaj je vezan sa poprečnim savijanjem u i sa torzijom ϑ.

Niže će biti izvedena diferencijalna jednačina za bočno izvijanje. Jednačine za u i ϑ su homogene. Ako su i konturni uslovi homogeni onda je bočno izvijanje grede mogućno samo za sopstvene vrednosti problema, tj. u i ϑ ostaju prvo nula kod gore opisane grede bez poremećaja. Uslov bočnog izvijanja se dobija – slično kao kod izvijanja štapa – ako se stavi da je jednaka nuli determinanta koeficijenta homogenih uslovnih jednačina za integracione konstante. Videćemo da i pri bočnom izvijanju postoji prava tačka račvanja elastične ravnoteže.

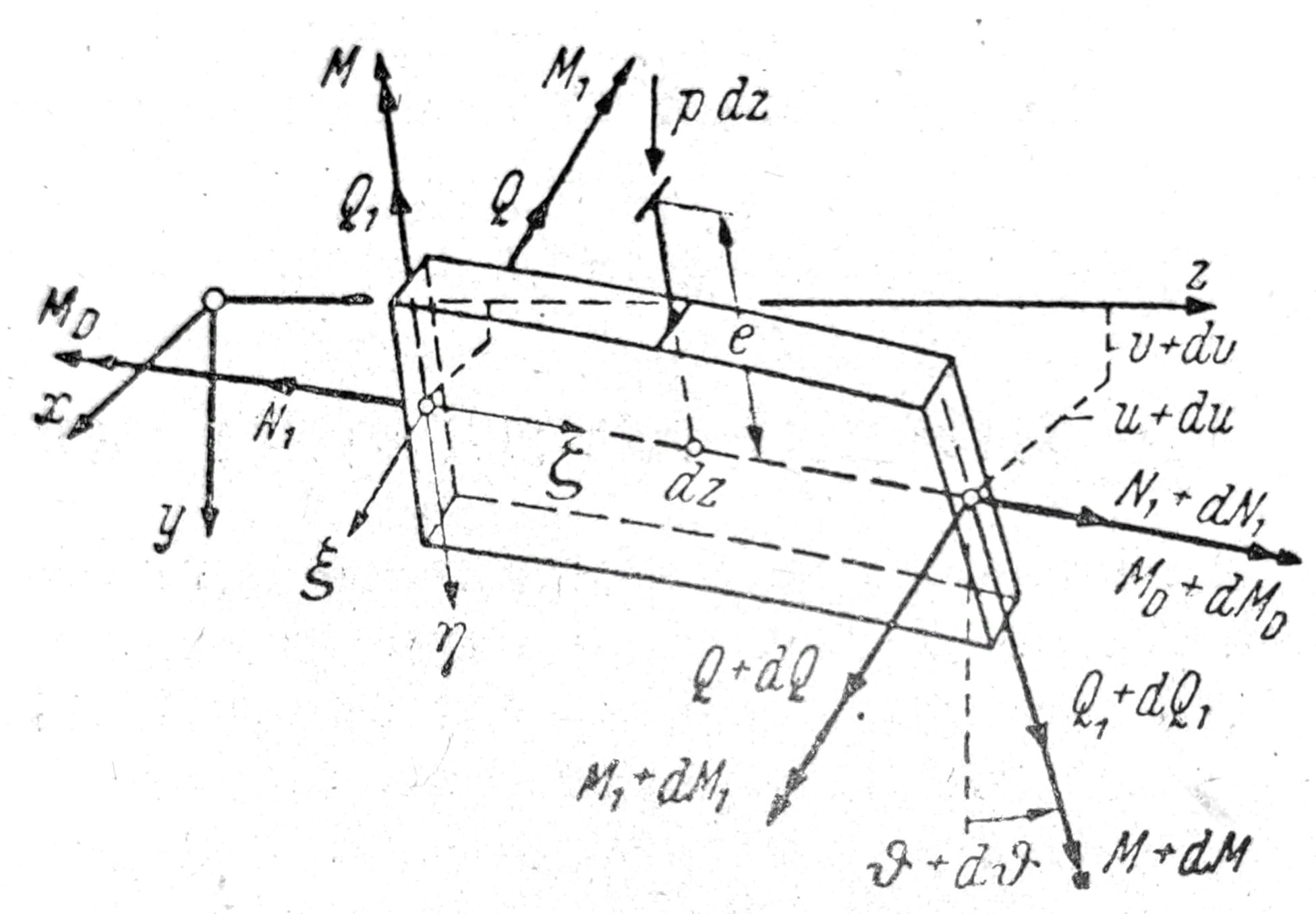
Sl. 1b

Na sl. 1b predstavljen je element grede dužine dz. Rezultante napona N₁, Q₁, M₁, kao i krivina κ₁ zavise od opterećenja i konačne su veličine. Q, M, M_D su nula u prvobitnom ravnotežnom položaju, a razlikovaće se od nule tek kad nastupi bočno izvijanje. Krajnje veličine, koje se odnose na početak bočnog izvijanja, beskonačno su male, kao i odgovarajuće deformacije κ i dϑ/dz.

Oba krajnja preseka elementa dz leže u normalnoj ravni na dvojno zakrivljenu osu štapa i biće uvijene u ovim normalnim ravnima.

Pošto nas – kao i kod izvijanja štapa – u prvoj liniji interesuje veličina kritičnog opterećenja, dakle početak bočnog izvijanja, a manje veličina deformacija, to možemo proizvode veličina Q, M, M_D sa κ ili ϑ’ da zanemarimo kao male veličine drugog reda. Stoga ćemo radi daljeg uprošćenja i glavnu krivinu κ₁ da pretpostavimo kao beskonačno malu i biće tretirana kao κ i ϑ’.

Napomena: Uticaj od κ₁ ima i teorijski da se proceni u jednostavnom specijalnom slučaju (konstantni moment savijanja M kao opterećenje). U većini potreba građevinske tehnike može da se zanemari κ₁. Može, recimo, da zamislimo kao da je greda za dotični slučaj opterećenja tako „nadvišena“ da je za kritično opterećenje baš κ₁=0.

Iz ravnoteže komponenata sila u pravcima ξ, η, ζ i momentnim uslovima u odnosu na iste te ose dobija se posle spomenutih zanemarivanja

Q’ + N₁u’’ – Q₁ϑ’ + pϑ = 0,   (1a)

Q₁’ + p = 0,   (1b)

N₁’ = 0,   (1c)

M₁’ – Q₁ = 0,   (1d)

M_D’ + Q + M₁ϑ’ = 0,   (1e)

M_D’ – M₁u’’ + pe ϑ = 0.   (1f)

Iz jedn. (1c, d i b) dobija se

N₁ = const.,

Q₁ = M₁’,     (2)

p = - Q₁’ = - M₁’’.

Eliminisanjem Q₁ iz jedn. (1a) dobija se

Q’ = (M₁’ ϑ)’ – N₁u’’.   (3a)

Iz jedn. (1e) biće time eliminisano Q, zatim u ’’ putem u’’ = (M_D’ + pe ϑ)/M₁

(M+M₁ ϑ)’’ – N₁/M₁ ∙ (M_D’ + pe ϑ) = 0.   (3b)

Da se dobije diferencijalna jednačina za ϑ uvešće se sledeći odnosi između momenata i deformacija

M₁ = -B₁∙v’’,   (4a)

M = +B∙u’’,   (4b)

M_D = +C∙ϑ’ – EC*∙ ϑ’’’,   (4c)

gde označava B₁=EI_x i B=EI_y krutosti protiv savijanja grede, C krutost protiv uvijanja, a C* otpor krivljenju. Kod naših daljih računa izostavićemo članove sa C* radi uporšćenja. Trebaju li jednačine da se primene npr. na I-profile, onda je potrebno dopuniti ih na odgovarajući način. Zanemarenje člana v’’ znači isto što i pretpostavka B₁=∞.

Ako se eliminišu M i M_D pomoću jedn. 4 dobija se diferencijalna jednačina za bočno izvijanje grede konstantnog preseka

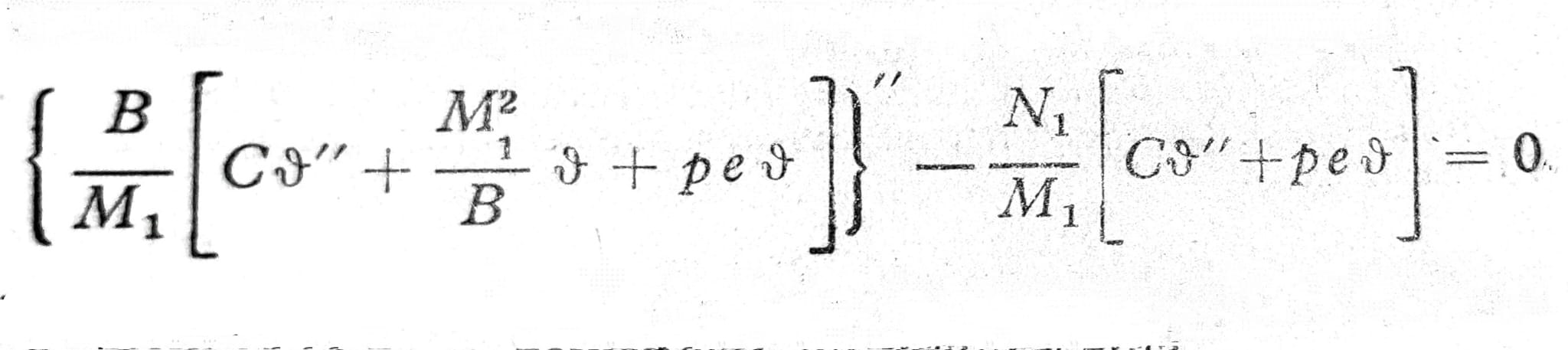
Diferencijalna jednačina (5) je homogena i četvrtog reda po ϑ. M₁ je poznata funkcija od z u zavisnosti od opterećenja.

 

Greda sa konstantnim momentom savijanja

Neka bude p=N₁=0, osim toga M_x=ɱ=const. Presek je bez flanše (zbijen) i greda dugačka u odnosu na dimenzije poprečnog preseka, tako da možemo staviti da je C*=0. Tada se uprošćava jedn. (5), zbog M₁=ɱ, pa je:

ϑ’’’’ + ɱ²/BC∙ ϑ’’ = 0,   (6)

ili sa kraćenicom λ²=ɱ²/BC

ϑ’’’’ + λ² ϑ = 0.   (6a)

a) Greda sa viljuškastim osloncem na oba kraja

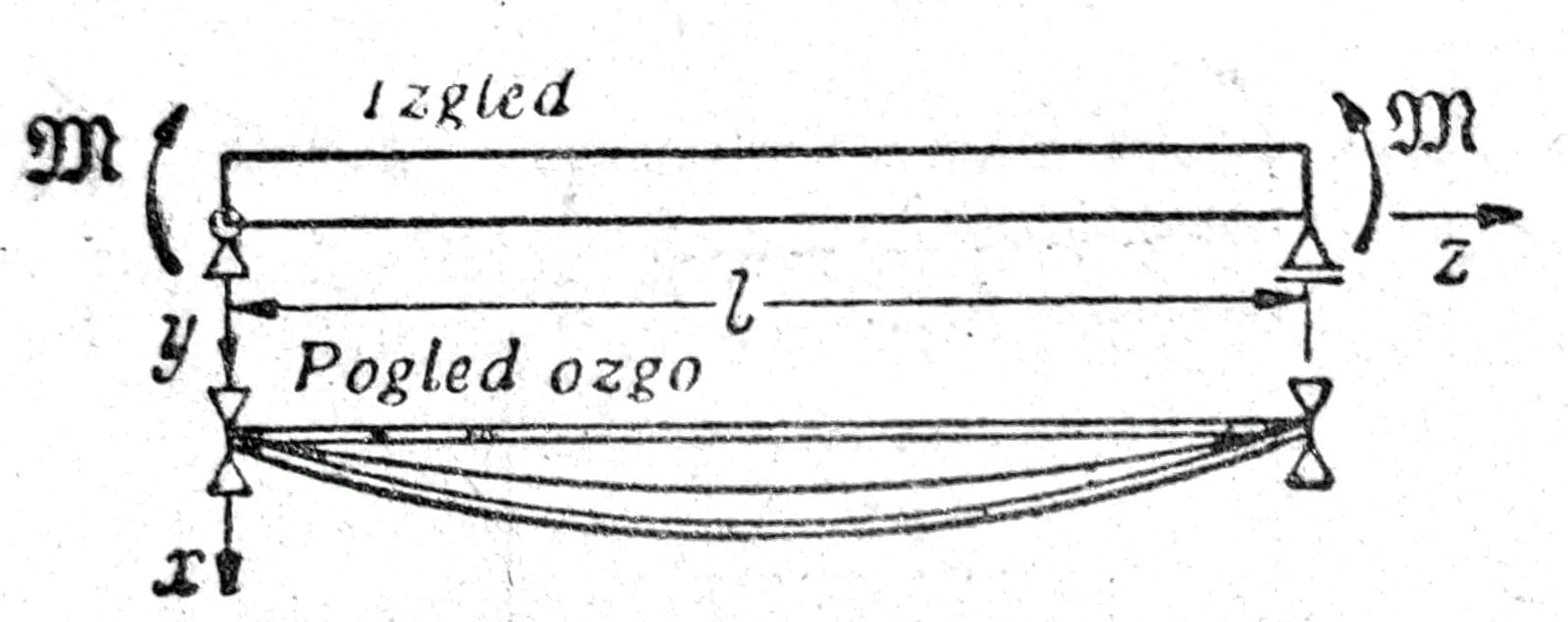
Sl. 2

Oslanjanje kod z=0 i z=l je u vidu viljuški (sl. 2), koje omogućuju ugibe u i v, ali sprečavaju okretanje krajnjih preseka; ϑ=0. Pošto u pravcu x nema uklještenja (tj. M=0, ili prema jedn. (4) takođe u’’=0), proizilazi iz jedn. za u’’: M_D’=0 i time iz jedn. (4c) kao drugi konturni uslov ϑ’’=0.

Opšte rešenje jedn. (6a) je

ϑ(z) = A₁∙sinλz + A₂∙cosλz + A₃∙λz + A₄.   (7)

Iz konturnih uslova se dobije

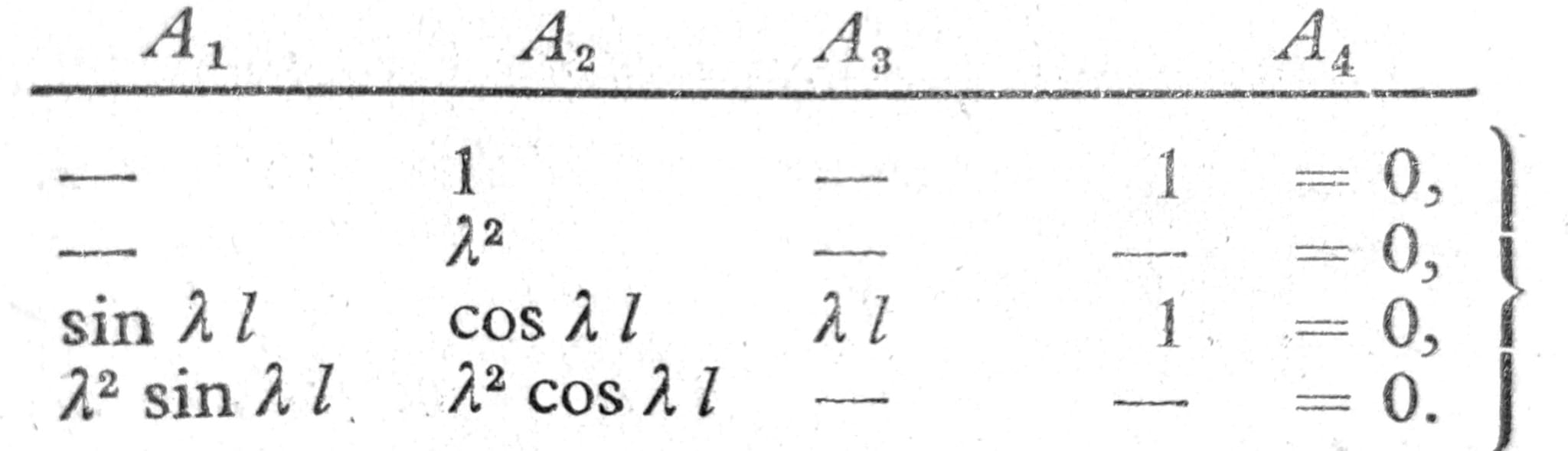
Ovaj homogeni sistem jednačina ima:

• Trivijalno rešenje A₁ = A₂ = ∙∙∙ = 0, čemu odgovara ϑ=0, u’’=0 ili u=0, pri čemu se greda bočno ne izvija.
• Sopstvena rešenja prema Δ=0 ili sin λl=0. Koreni ovog uslova bočnog izvijanja su λl=nπ (sa n=1,2,3,∙∙∙) i odgovarajuća kritična momentna opterećenja

ɱ_K = √BC ∙ nπ/l.   (8b)

Najmanji moment bočnog izvijanja

_minɱ_K = √BC ∙ π/l   (8c)

nastaje na n=1. Odgovarajuće rešenje je primenom jedn. (1f):

ϑ(z) = A₁ ∙ sin πz/l   (8d)

u(z) = C/ɱ_K ∙ ϑ(z).

b) Ostalli slučajevi bočnog izvijanja

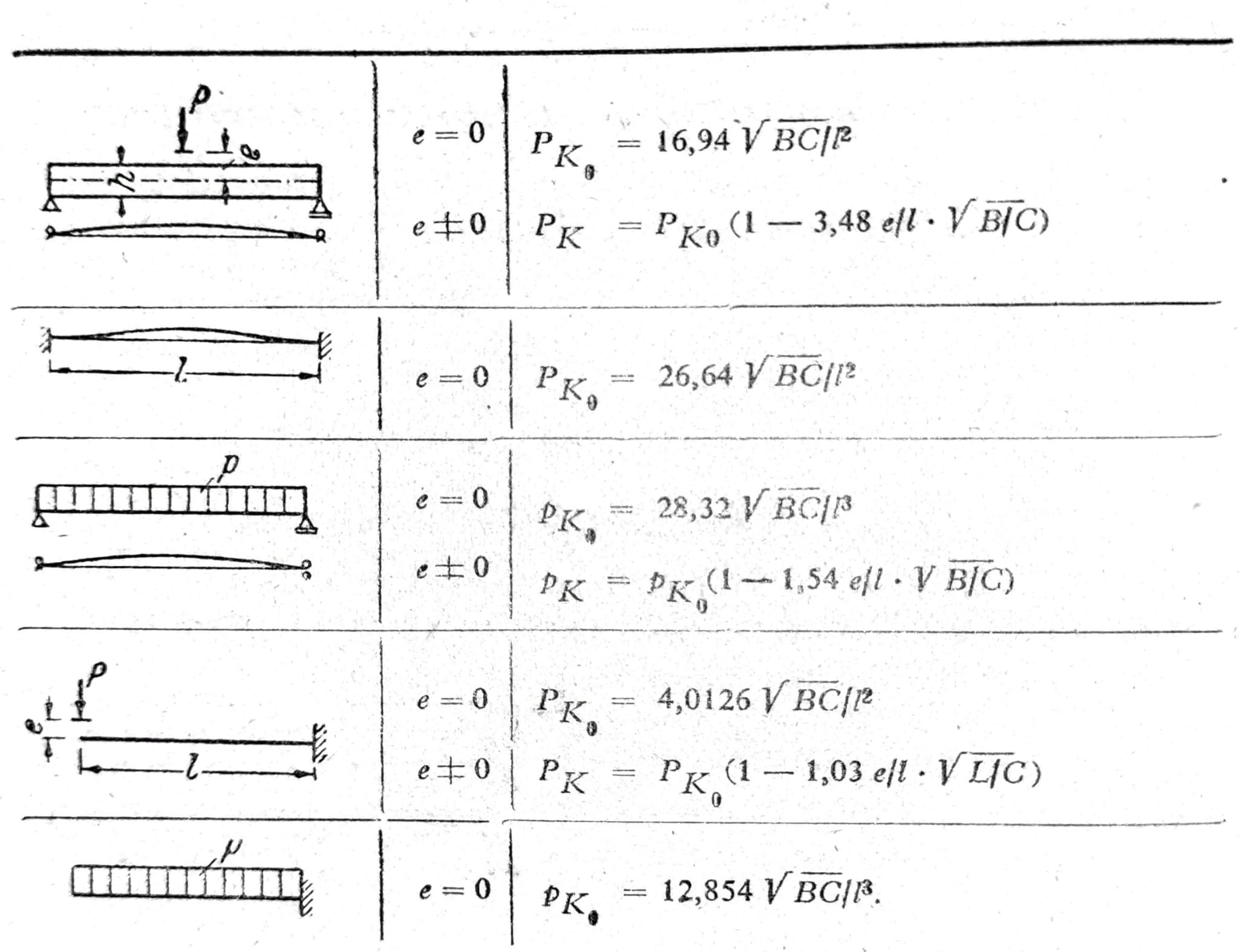
c) Bočno izvijanje usled momenta savijanja i pritiskajuće sile

Za primer pokazan na sl. 3 je N₁=-D (pritisak), p=0, zatim je stavljeno C*=0. Tada se diferencijalna jedn. (5) uprošćava i glasi

ϑ’’’’ + λ² ϑ’’ = 0,   (9)

gde je λ² = ɱ²/BC + D/B.   (9a)

Rešenje diferencijalne jednačine (9) dato je opet jedn. (8), samo sada λ označava drugu vrednost.

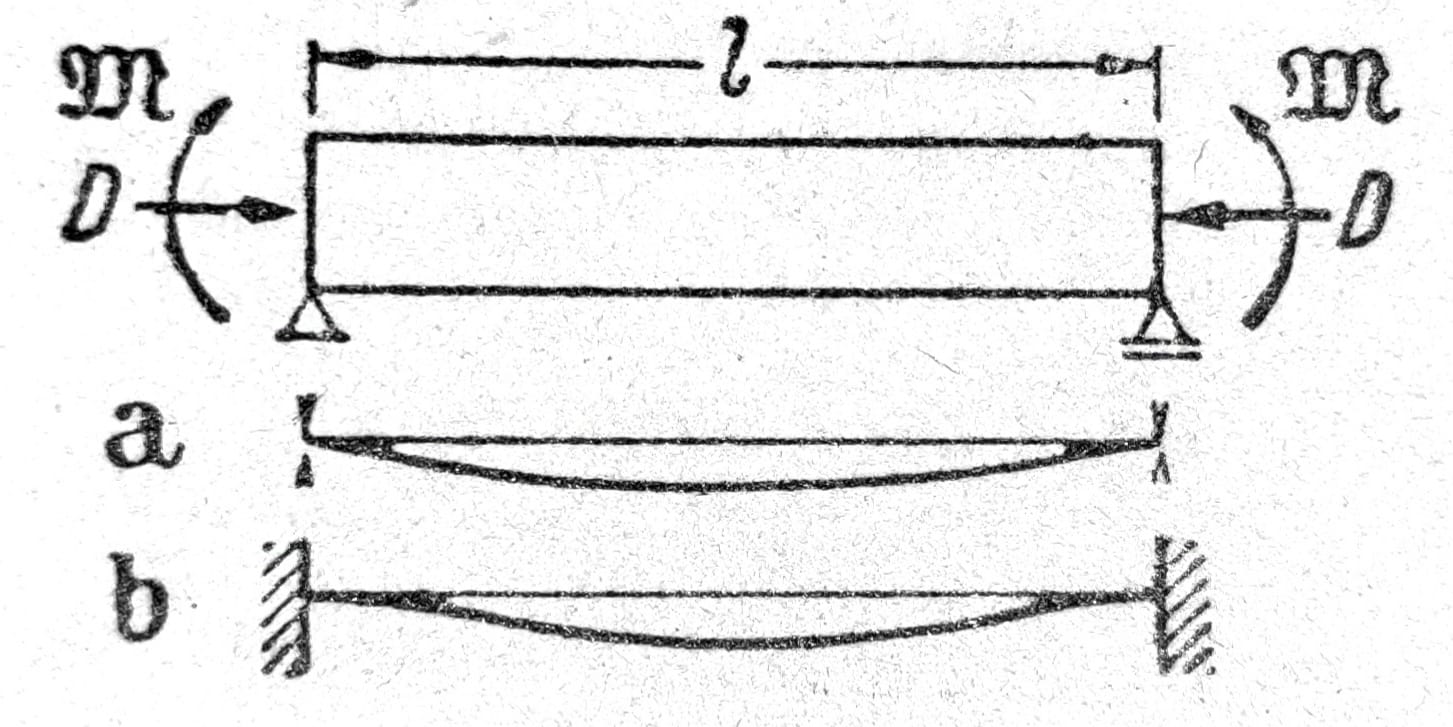
Sl. 3

Za primer sl. 3 važe kao i za a) konturni uslovi ϑ=0 i ϑ’’=0 za z=0 i z=l. Prema tome su i uslovne jednačine za A₁ formalno iste a takođe i uslov bočnog izvijanja Δ=sin λl=0. Kritično opterećenje zadovoljava odnos λl=nπ (n=1,2,3) i najmanja vrednost je

ɱ_K²/BC + D_K/B = (π/l)².   (10)

Za D=0 dobija se odatle moment bočnog izvijanja prema jedn. (8c) i za čisto pritiskajuće opterećenje (ɱ=0) Euler-ova sila izvijanja D_K=B(π/l)².

Na sl. 3 predstavljeni slučaj ima da se označi kao ekscentrično savijanje u ravni y-z. Napred posmatrani slučaj stabilnosti je, dakle, krivljenje iz ravni savijanja vezano sa bočnim savijanjem u i torzijom ϑ.

Ako su oba kraja uklještena (ϑ=0 i ϑ’=0) onda se iz konturnih uslova, pomoću Δ=0, dobija uslov bočnog izvijanja

λl ∙ sin λl = 2(1-cos λl),    (11)

sa korenima λl=mπ (m=2,4,∙∙∙) i silama bočnog izvijanja

ɱ_K²/BC + D_K/B = (2π/l)².