Struktura i podela nosača. Uslovi stabilnosti
Elementi nosača. Unutrašnja i spoljašnja stabilnost
Elementi nosača su:
Prosti štapovi koji su sposobni da prenesu samo sile zatezanja ili pritiska čija se napadna linija poklapa sa osom štapa. To uslovljava da štapovi u čvorovima budu vezani zglobovima u kojima nema trenja, a da se spoljašnje sile napadaju u čvorovima. Nosači koji se sastoje samo od prostih štapova nazivaju se rešetke.
Štapovi optporni na savijanje – grede – mogu da prenesu kako sile čije se napadne linije poklapaju sa osom štapa, tako i sile čije su napadne linije paralelne sa osom štapa ili proizvoljno nagnute prema njoj. Grede primaju normalne sile, transverzalne sile, momente savijanja i u datom slučaju momente torzije. One u čvorovima mogu biti vezane zglobno ili pomoću krutih uglova.
Oslonci i uklještenja sprečavaju pomeranja nosača prema stalnim tačkama u ravni ili prostoru. Svaki oslonac je sposoban da prenese silu u određenom pravcu koji prolazi kroz odlonjeni čvor. Ako u oslonjenom čvoru – oslonačkoj tački – postoji samo jedan oslonac, on se naziva pokretno ležište prostornog nosača. Ako je čvor oslonjen sa dva oslonca, on se naziva nepokretno ležište ravnog nosača, odn. linijsko ležište prostornog nosača. Nepokretno ležište prostornog nosača zahteva tri oslonca.
Svako uklještenje štapa otpornog na savijanje u stanju je da prenese moment uklještenja koji leži u određenoj ravni. Sa uklještenjem je u većini slučajeva vezano nepokretno ležište, tako da kod ravnog nosača postoje dva oslonca i jedno uklještenje, a kod prostornog nosača tri oslonca i tri uklještenja. Na mestima oslanjanja i uklještenja mogu se pojaviti pomeranja i obrtanja određene veličine.
Potreban broj elemenata za stabilnost nosača dobija se iz uslova za unutrašnju i spoljašnju stabilnost. Nosač je unutrašnje stabilan kada je međusoban položaj čvorova nosača osiguran dovoljnim brojem štapova tako da se on može menjati samo onda kada pojedini ili svi štapovi menjaju dužine. Unutrašnje stabilan ravan nosač naziva se kruta ploča. Nosač je spoljašnje ili potpuno stabilan kada se međusoban položaj čvorova i njihov položaj prema stalnim tačkama ravni, odn. prostora može menjati samo u toj meri kolike su promene dužine štapova, pomeranja oslonaca ili obrtanja uklještenja.
Ravni nosači
Minimalan broj štapova potreban za unutrašnju stabilnost i minimalan broj štapova i oslonaca potreban za spoljašnju stabilnost rešetke sa s štapova, a oslonaca i k čvorova je:
s = 2k – 3
s + a = 2k, (3 ≤ a)
Prvi uslov je ispunjen kada je nosač formiran polazeći od jednog štapa nadovezivanjem daljih čvorova sa po dva štapa, pri čemu štapovi kojima je priključen jedan čvor ne smeju ležati na istoj pravoj.
Nosač sa s1 prostih štapova, s2 štapova otpornih na savijanje, e krutih uglova, a1 oslonaca, a2 uklještenja i k čvorova je unutrašnje, odn. spoljašnje stabilan kada je:
s1 + s2 + e ≥ 2k – 3
s1 + s2 + e + a1 + a2 ≥ 2k, (a=a1 + a2 ≥ 3)
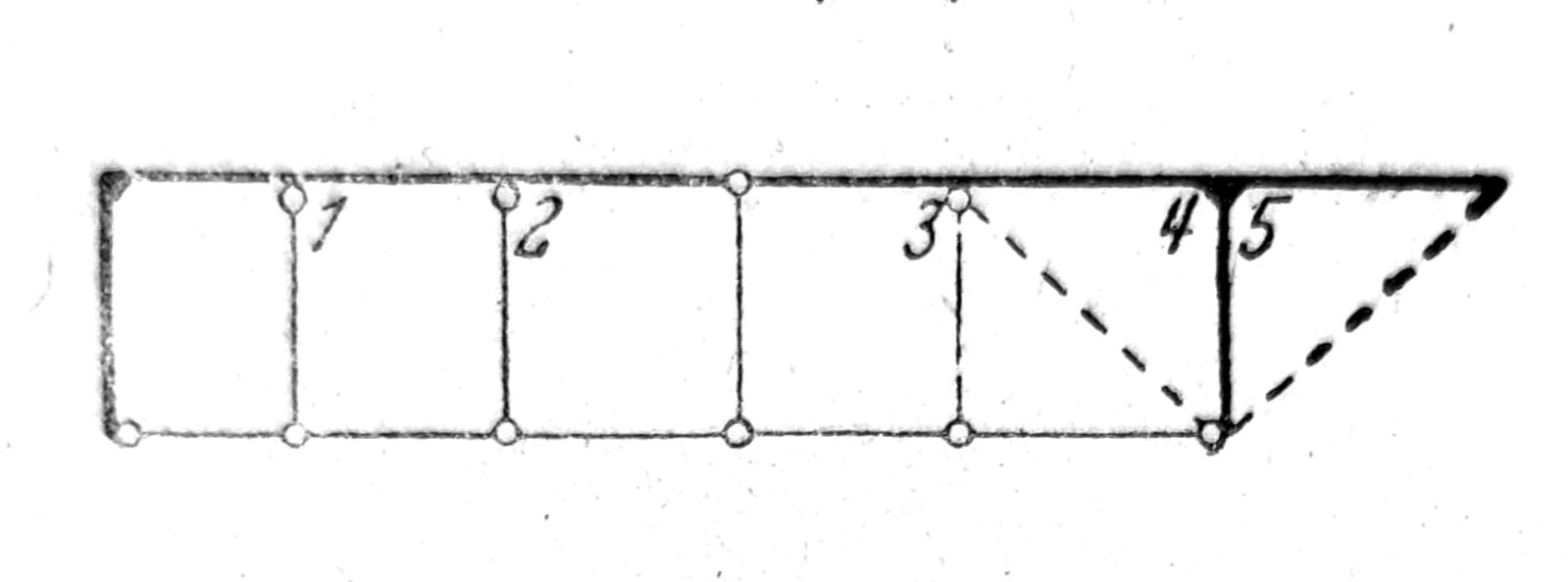
Sl. 1
Svaki krut ugao može se zameniti jednim prostim štapom. Ako su u jednom čvoru i štapova međusobno kruto vezani, broj krutih uglova u tom čvoru je i-1. Kada se prepusti štapova (konzole) ubroje u štapove, slobodne krajeve treba ubrojiti u čvorove. Nosač na sl. 1 sa s1=9, s2=7, e=5 (označeno na slici) i k=12 unutrašnje je stabilan. Kada krute uglove 4 i 5 zamenimo zglobovima i prostim štapovima, koji su na slici označeni isprekidanim linijama, tada je s1=11, s2=7, e=3, dok broj čvorova ostaje nepromenjen.
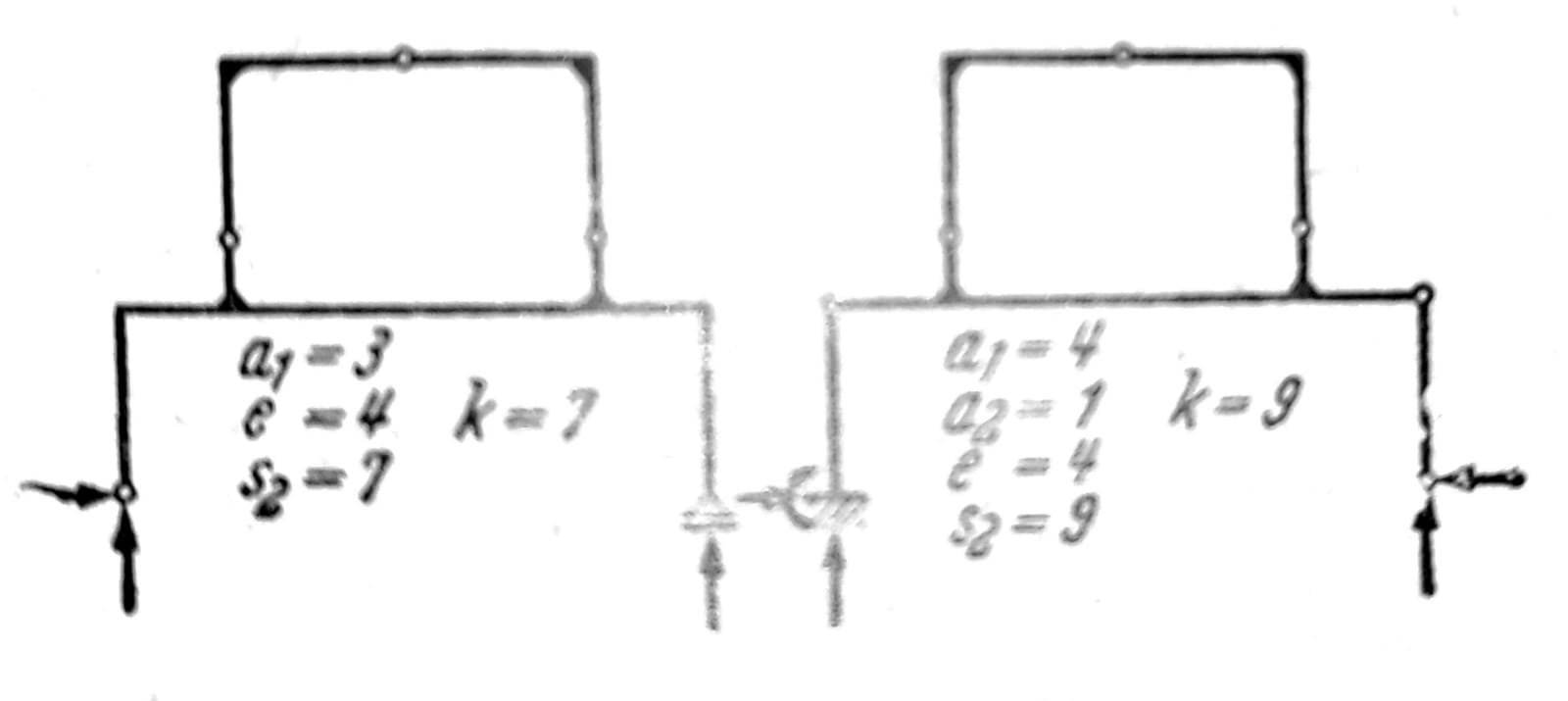
Sl. 2a i 2b
Ako se u jednom nosaču sa zahtevanim minimalnim brojem oslonaca pojedini štapovi ili kruti uglovi zamene osloncima ili uklještenjima, nosač gubi unutrašnju stabilnost, sl. 2a, b. Za takve nosače postoje i druge mogućnosti kako se stabilnost može ispitati. Ako je p broj krutih ploča nosača bez unutrašnje stabilnosti, pri čemu treba zapaziti da jedan jedini prost štap ili štap otporan na savijanje ispunjava uslove unutrašnje stabilnosti te može biti shvaćen kao kruta ploča, i ako je z broj međureakcija u zglobovima, spoljašnja stabilnost zahteva da je: a + z ≥ 3p. Broj međureakcija u zglobu u kome je vezano i ploča (sl. 3, 4, 5) je z=2(i-1).
Sl. 3 i 4, respektivno
Sl. 5
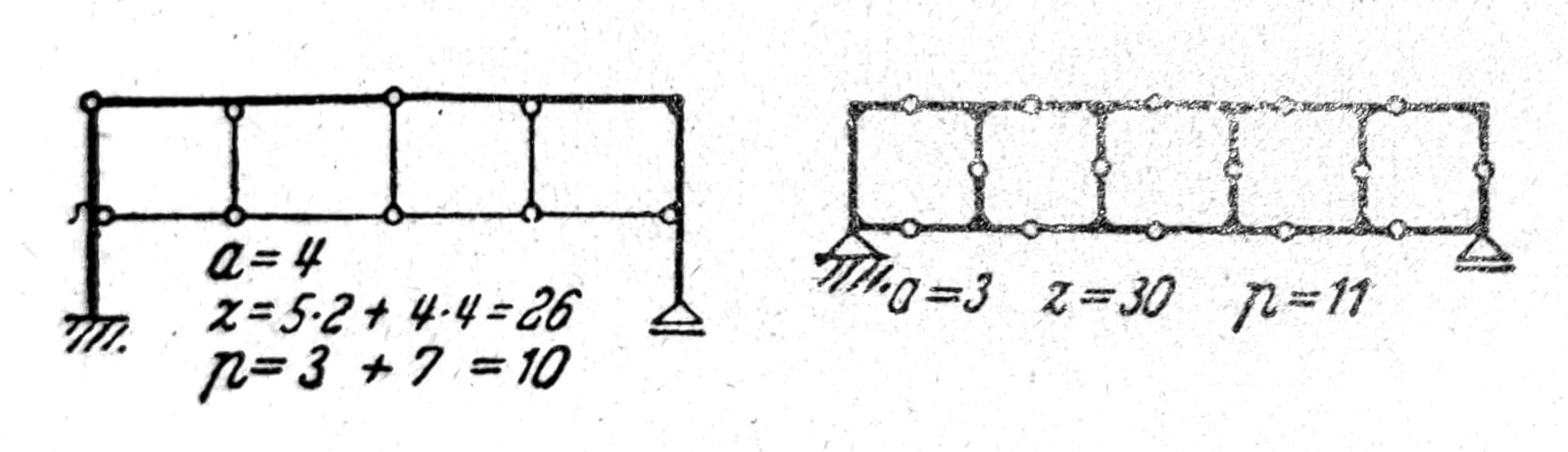
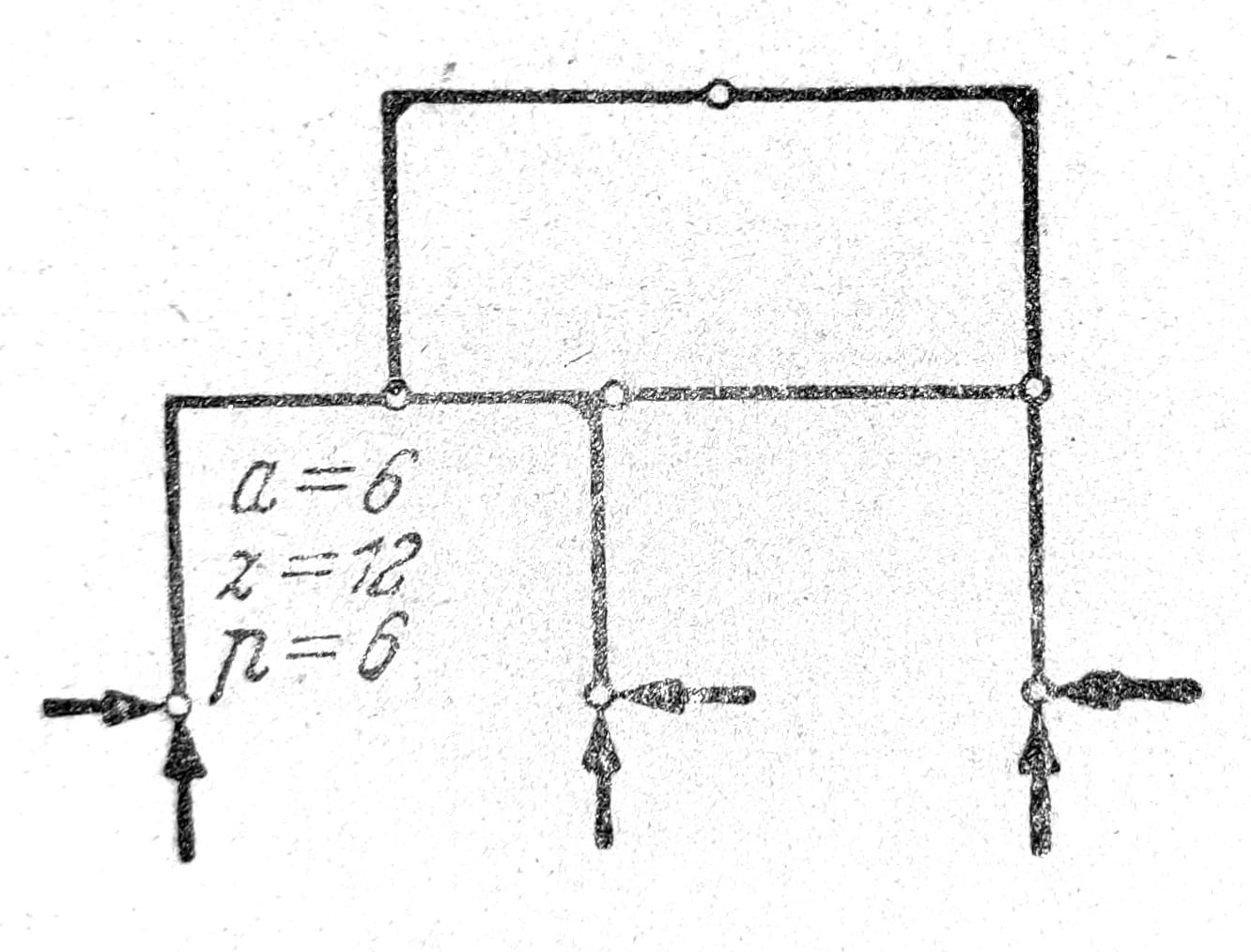
Okvir na sl. 6 je šest puta statički neodređen. Ako se prepusti, koji nemaju uticaja na stepen statičke neodređenosti, ubroje u štapove, treba uzeti u obzir i krute uglove kojima su oni za sistem vezani i slobodne krajeve prepusta ubrojati u čvorove (s=7, e=6, a=9, k=8). Kod ovih vrsta nosača prikladan oblik uslova za ispitivanje unutrašnje i spoljašnje stabilnosti je:
3s ≥ 3k-3; 3s+a ≥ 3k, (a≥3).
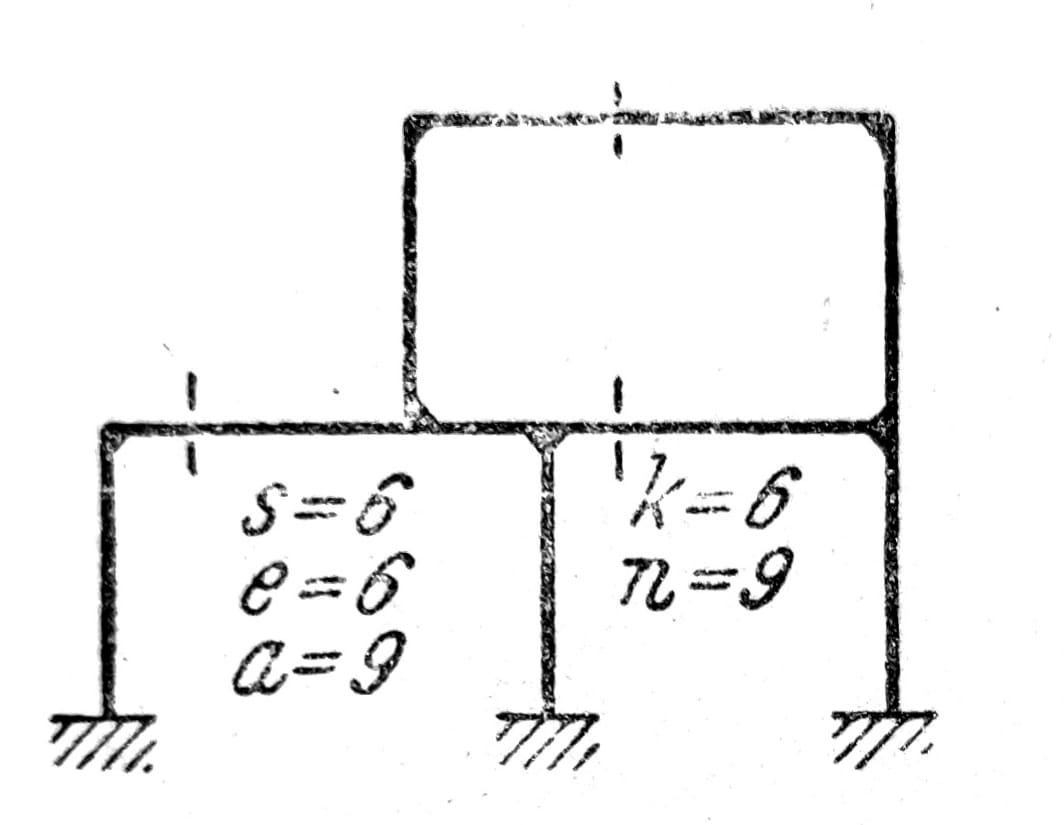
Pri tome prepusti ne smeju biti ubrojani u štapove. Često se u ovakvim slučajevima najbrže dolazi do zaključka o stepenu statičke neodređenosti nosača, presecanjem štapova ili isklljučivanjem statičkih veličina sve dotle dok ne preostane nesumnjivo stabilan, statički određen nosač. Sa tri preseka naznačena na sl. 7 isključene su po tri statičke veličine (normalna sila, transverzalna sila, moment savijanja).
Ako se u jednoj n0-puta statički neodređenoj ravnoj rešetki svi štapovi u čvorovima kruto vežu, stepen statičke neodređenost je
n = n0 + 2s – k.
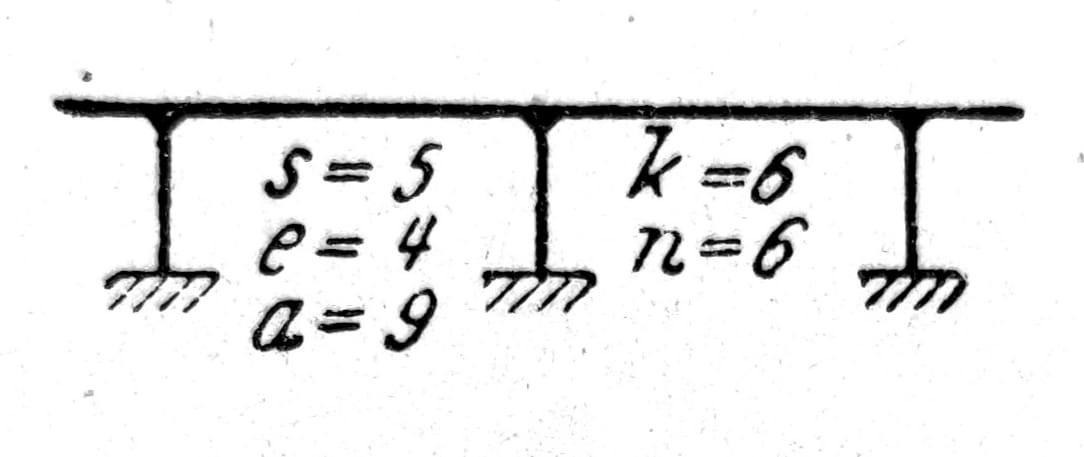
Sl. 6
Sl. 7
Prostorni nosači
Minimalan broj oslonaca za prostorne rešetke je a=6. Za unutrašnju i spoljašnju stabilnost važe sledeći uslovi:
s ≥ 3k – 6; s + a ≥ 3k, (a≥6).
Uslov za unutrašnju stabilnost je ispunjen kada su polazeći od jedne trougaone ploče dalji čvorovi u prostoru vezani sa po tri štapa koji ne smeju ležati u jednoj ravni. Na taj način nastaje prostorna rešetka prve vrste čija je karakteristika da uvek sadrži bar jedan čvor u kome su vezana samo tri štapa i da tu osobinu zadržava i onda kada se taj čvor sa odgovarajućim štapovima ukloni.
Nadalje, prostorne rešetke mogu se formirati povezivanjem trougaonih ploča na taj način da su dve i dve ploče vezane sa šest štapova pri čemu je svaki čvor vezan za susedne ploče sa po dva štapa. Veza dve ploče ili dve unnutrašnje stabilne prostorne rešetke može se ostvariti pomoću jednog zgloba i tri štapa koji ne prolaze kroz taj zglob. Najzad, tri trougaone ploče mogu se povezati sa 12 štapova i to sa po 4 štapa između svake ploče. Za unutrašnju, odn. spoljašnju stabilnost prostornih nosača kod kojih su svi štapovi kruto vezani na savijanje i uvijanje, moraju biti ispunjeno uslovi
6s ≥ 6(k-1); 6s + a ≥ 6k
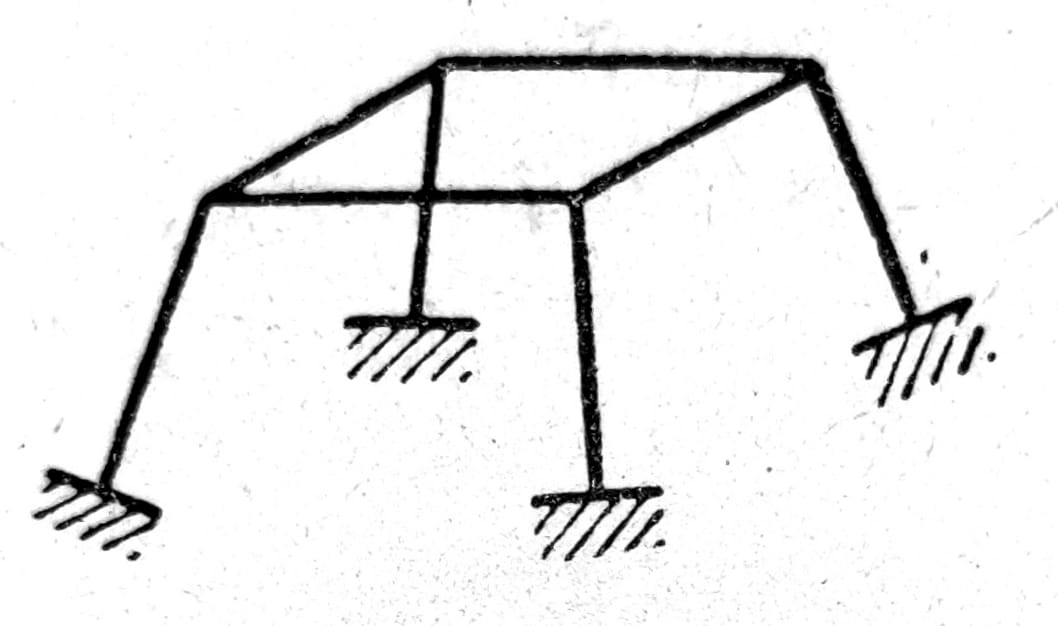
Prema tome, nosač na sl. 8 je 24 puta statički neodređen u šta se, kao i ranije, najlakše može uveriti kada se preseku četiri horizontalna štapa i na taj način u svakom preseku isključi šest nepoznazih (1 normalna sila, 2 transverzalne sile, 2 momenta savijanja i 1 torzioni moment). Ako uklonimo f veza ubacivanjem zglobova u štapove ili njihove veze, tada uslovi stabilnosti glase:
6s – f ≥ 6(k-1); 6s – f + a ≥ 6k.
Sl. 8
Opterećenje i reakcije. Zadaci statike.
Kod ravnih nosača moraju spoljašnje sile da leže u ravni nosača, kod prostornih nosača one mogu imati proizvoljan položaj. Kod rešetki se pretpostavlja da opterećenje napada u čvorovima.
Aktivne sile izazivaju otpore spoljašnjih elemenata, reakcije oslonaca C u osloncima i momente uklještenja E u uklještenjima. Otpori unutrašnjih elemenata nosača – presečne sile – su: aksijalne sile S u prostim štapovima; u štapovima otpornim na savijanje i uvijanje normalne ili podužne sile N, momenti savijanja M, momenti uvijanja ili torzioni momenti T i transverzalne sile Q. Otpore elemenata mogu da izazovu i promene temperature i popuštanja oslonaca.
Dimenzionisanje pojedinih elemenata i određivanje napona koji se u njima pojavljuju zadatak je Otpornosti materijala. Pri određivanju statičkih veličina primenjeni materijal od značaja je samo utoliko što od njega zavisi stalno opterećenje. Druge osobine materijala ulaze u račun jedino onda kada je reč o uticaju pomeranja oslonaca ili promena temperature (skupljanje, tečenje) ili kada treba sračunati deformacije. U opštem slučaju nosače treba ispitati za razne slučajeve opterećenja koja se ne moraju pojavljivati istovremeno (stalan teret, korisno opterećenje, opterećenje vetrom, opterećenje snegom). Pod pretpostavkom da su elastične deformacije tako male da se u odnosu na dimenzije sistema mogu zanemariti – a to je redovito slučaj – važi princim superpozicije, prema kome se smeju pojedini slučajevi opterećenja i drugi uticaji posebno ispitivati i tako sračunate vrednosti za statičke ili geometrijske veličine sabrati, uz određenu korekciju vrednosti kroz parcijalne koeficijente sigurnosti za stalno i promenljivo opterećenje (povoljno ili nepovoljno).
Rešenje statičkog zadatka statički određenih nosača
Nepoznate i raspoložive jednačine
U jednoj statički određenoj rešetki nepoznate su a reakcija oslonaca i s aksijalnih sila za čije određivanje kada rešetka ima k čvorova stoji na raspolaganju 2k jednačina (∑X=0 i ∑Y=0) u ravni i 3k jednačina u prostoru. U ravnom nosaču nepoznate se mogu svesti na s1 aksijalnih sila prostih štapova, s2 normalnih sila štapova otpornih na savijanje, e momenata savijanja u krutim uglovima, a1 reakcija oslonaca i a2 momenata uklještenja. Transverzalne sile treba odrediti iz momenata na krajevima štapova i spoljašnjih sila koje napadaju između čvorova. U čvoru iz koga i kruto vezanih štapova polaze ka susednim čvorovima dovoljno je poznavati i-1 momenta – što odgovara broju krutih uglova – jer za određivanje još jednog nepoznatog momenta u svakom takvom čvoru stoji na raspolaganju uslov ravnoteže ∑M=0. Za određivanje s1 + s2 + e + a1 + a2 nepoznatih preostaje još 2k uslova ravnoteže.
Uslovi ravnoteže spoljašnjih sila na ravnim nosačima
Reakcije oslonaca ploče oslonjene na jedno nepokretno i jedno pokretno ležište (sl. 9) grafički se dobijaju pomoću poligona sila. Napadna linija sile B poznata je i ima pravac oslanjanja u toj tački, a napadna linija sile Ka mora prolaziti kroz presek sila B i P. Računski se iz uslova Ma = 0, H = 0 i Mb = 0 postupno određuju sile B, C i A. Oslanjanje ploče na tri pokretna ležišta (sl. 10) ispravno je samo onda kada se napadne linije reakcija ne seku u jednoj tački. Reakcije se određuju grafički pomoću poligona sila ili računski pomoću momentnih jednačina u odnosu na tačke u kojima se seku dve i dve napadne linije sila.
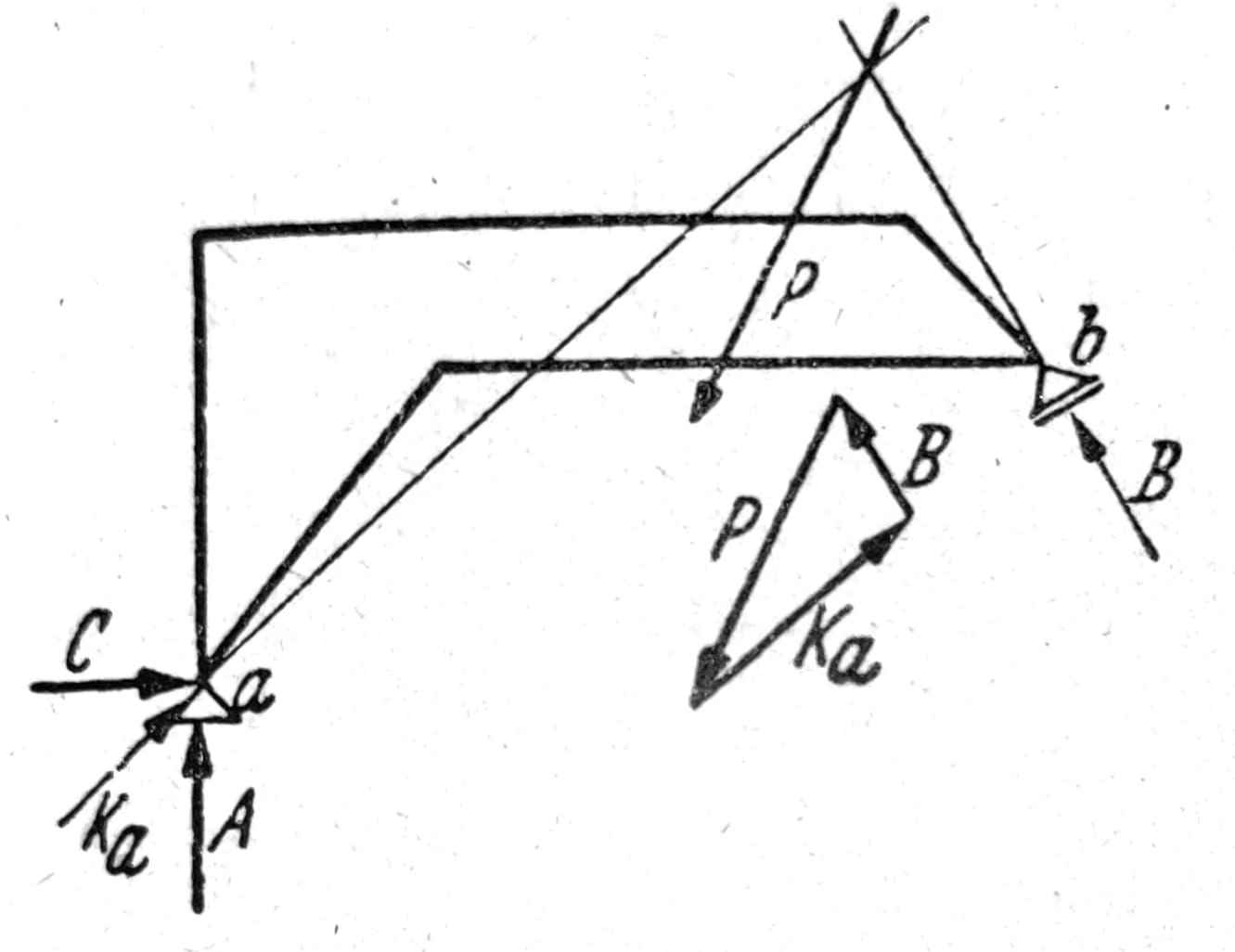
Sl. 9
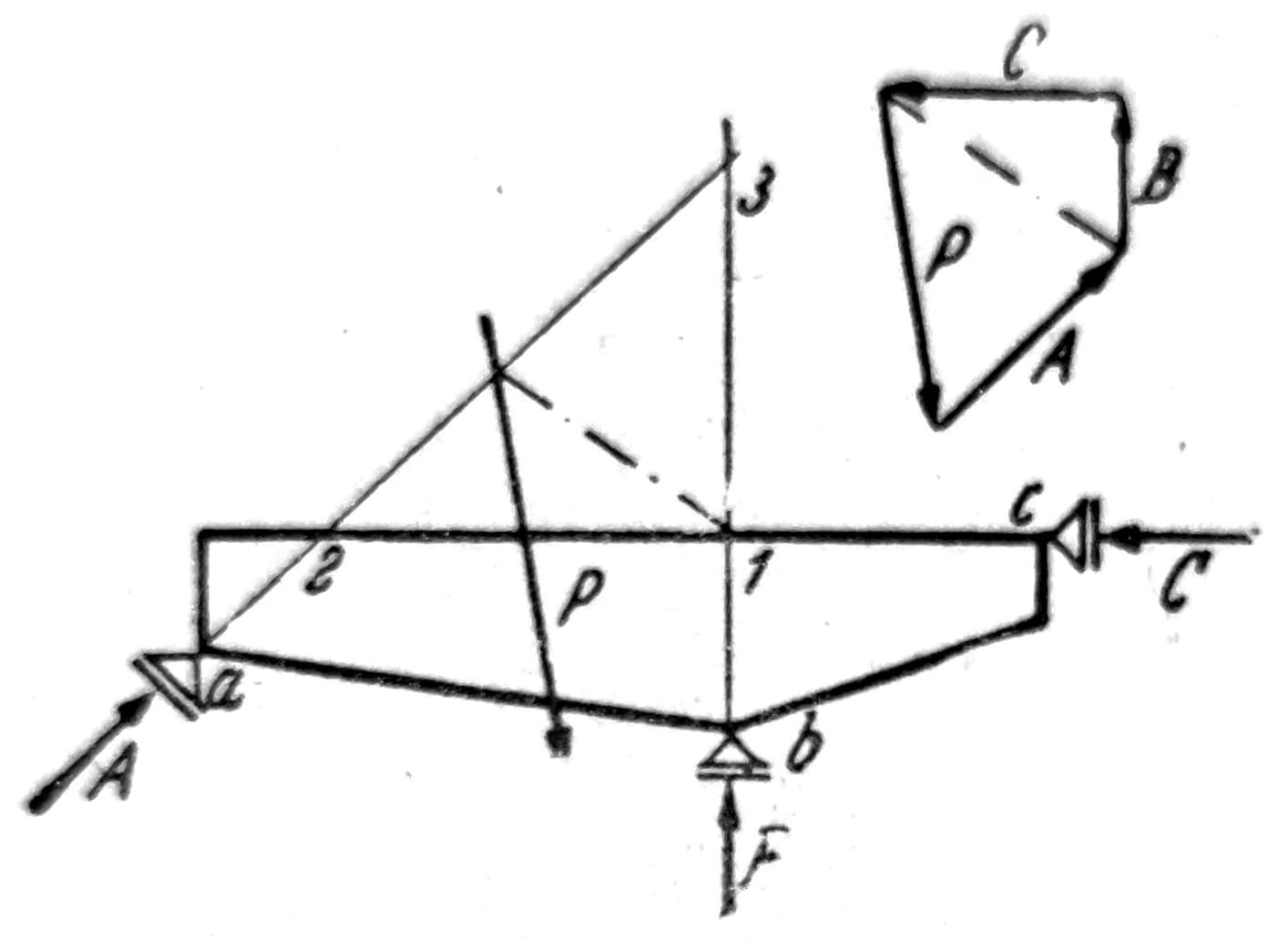
Sl. 10
Kod statički određenih nosača bez unutrašnje stabilnosti pored uslova ravnoteže spoljašnjih sila u celini se uvode i uslovi za zglobove kojima se izražava zahtev da zglobovi ne mogu da prime momente savijanja. Prema tome, napadna linija reakcije Ka okvira sa tri zgloba na sl. 11 mora prolaziti kroz zglob g, a desna ploča može biti u ravnoteži samo onda kada se tri sile koje na nju napadaju (P, Kb i sila u zglobu = Ka) seku u jednoj tački. Da bi se dobili uslovi ravnoteže koji sadrže samo po jednu nepoznatu zgodno je računati sa vertikalnim komponentama reakcija A i B i komponentama C i D duž prave koja spaja oslonačke tačke. Iz uslova Mb = 0 i Ma = 0 dobijaju se sile A i B, a iz uslova za zglob Mg = 0 za sile koje napadaju levu ploču dobija se sila C, a za sile na desnoj ploči sila D. Na sličan način određuju se reakcije oslonaca okvira na sl. 12. Za opterećenje koje je ovde zadato najbrže se dolazi do rezultata grafički. Nosač sa zglobovima prema sl. 13. Horizontalne komponente spoljašnjih sila koje na nosač napadaju prima nepokretno ležište, sila F dobija se iz ∑H=0. Ploča II se oslanje u tačkama g1 i g2 na ploče I i III, a ploča IV u g3 na III. Vertikalne sile u zglobovima G1, G2, G3 i reakcija E određuju se iz uslova ravnoteže ploče II odn. IV, a zatim se postupno određuju reakcije A, B, C i D.
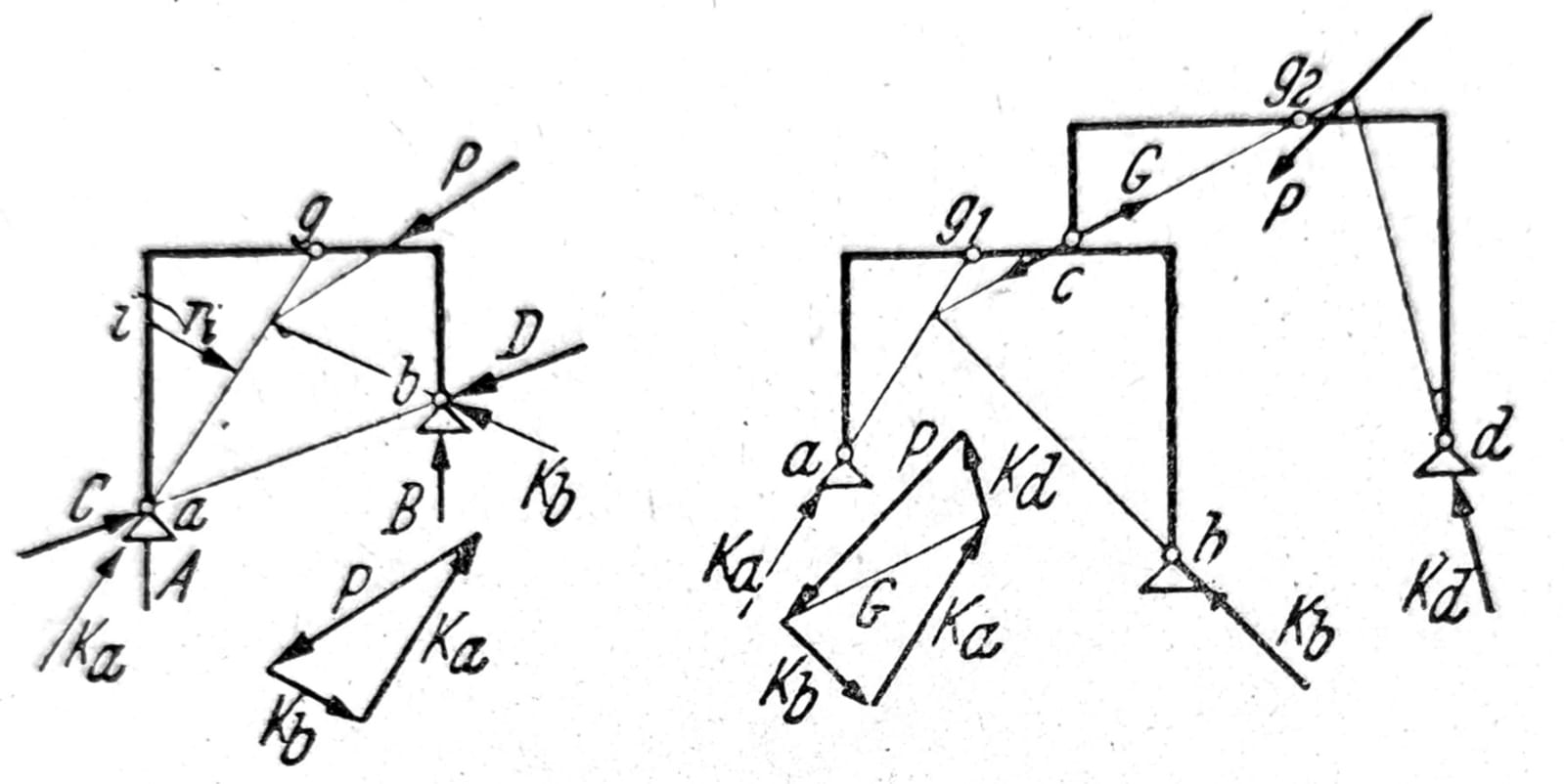
Sl. 11 i 12, respektivno
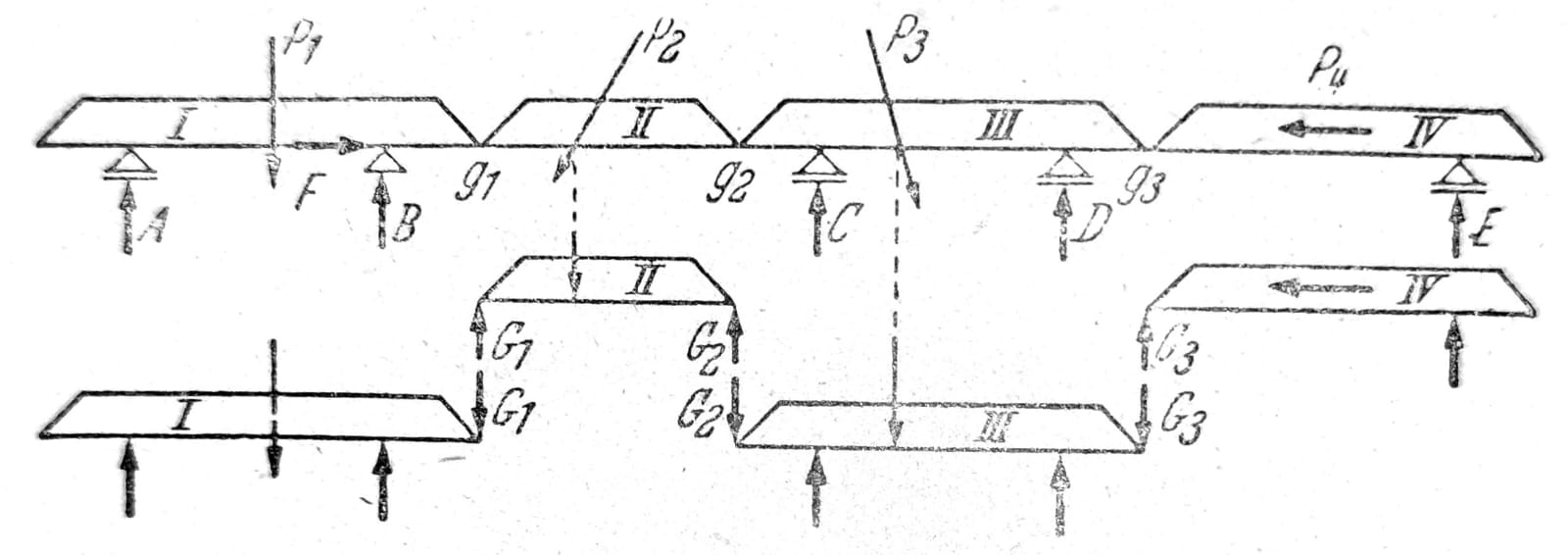
Sl. 13
Određivanje unutrašnjih statičkih veličina
Aksijalne sile S prostih štapova se po pravilu smatraju pozitivnim kada su sile zatezanja, a negativnim kada su sile pritiska. Na sličan način utvrđuje se znak normalne sile N u gredi. Normalna sila Ni na mestu i je komponenta paralelna sa tangentom na osovinu grede u tački i rezultante R svih sila koje napadaju na gredu s jedne strane od tačke i. Transverzalna sila Qi je komponenta normalna na osovinu štapa u tački i iste te rezultante, a moment savijanja Mi je moment te rezultante (sl. 14). Određivanje veličina N, Q i M vrši se redovno iz pojedinačnih sila i njihovih komponenata paralelnih i upravnih na osovinu štapa ne određujući rezultantu R. Konvencija pozitivnih smerova prikazana je na sl. 15.
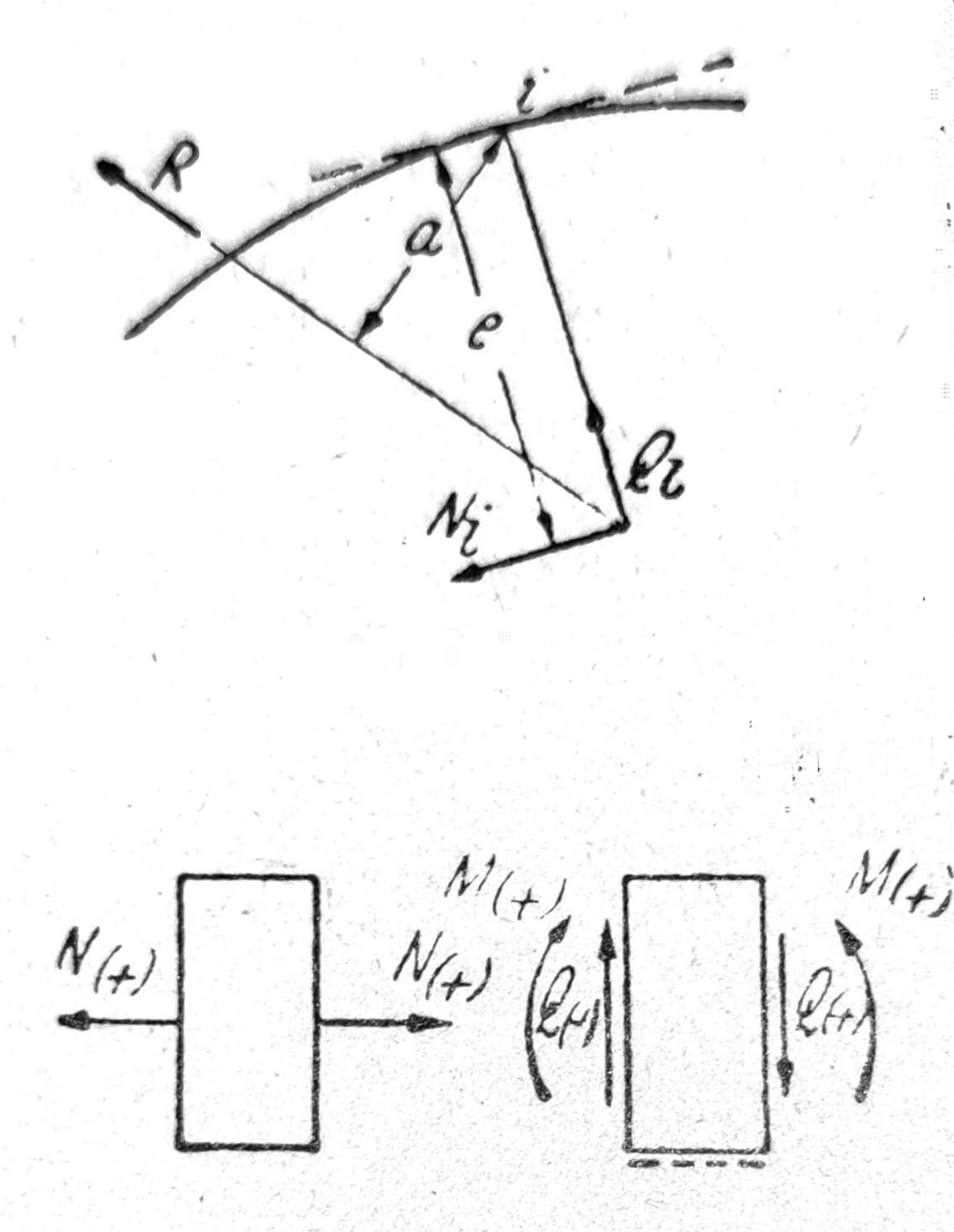
Sl. 14 i 15, respektivno
Pošto su grafički određene reakcije oslonaca, normalne sile, momenti savijanja i transverzalne sile mogu se odrediti iz poligona sila i plana u kome su sile zadate po položaju. Na primer, u levom stubu okvira na tri zgloba na sl. 11 vertikalna komponenta sile Ka je normalna sila (negativna), horizontalna komponenta je transverzalna sila (negativna), a Mi = Kari moment savijanja, negativan kada se momenti koji na unutrašnjoj strani izazivaju zatezanja smatraju pozitivnim.
U svakom čvoru u kome su štapovi vezani zglobno moraju biti ispunjeni uslovi ∑X=0, ∑Y=0. Rešetke koje su formirane na najjednostavniji način – povezivanjem čvorova sa po dva štapa – imaju uvek najmanje jedan čvor u kome se sutiču samo dva štapa. Uklanjanjem ovakvih čvorova ova osobina ostaje održana. Sračunavanje aksijalnih sila u štapovima može se sprovesti postupnim rešavanjem po dve jednačine sa po dve nepoznate.
Grafičko rešenje se dobija konstrukcijom plana sila (Cremana plan) prema sl. 16. Spoljašnje sile P1 do P6 stoje u ravnoteži. Sile u štapovima Si određuju se postupno polazeći od tačke 1 i idući od čvora do čvora po redu kako su obeleženi. Obeležavanje sila je takođe izvršeno po redu kojim se one određuju. Svakom čvoru odgovara poligon sila sa neprekidnim smerom strelica, iz koga slede znaci sila u štapovima. Ako se kroz nosač načini presek i ako se na mestima na kojima su štapovi presečeni sile koje u tim štapovima deluju nanesu kao spoljašnje sile, svaki deo rešetke je u ravnoteži. Na tome se zasnima Culmann-ov postupak kojim se sila u proizvoljnom štapu može odrediti grafički nevezano od ostalih sila.
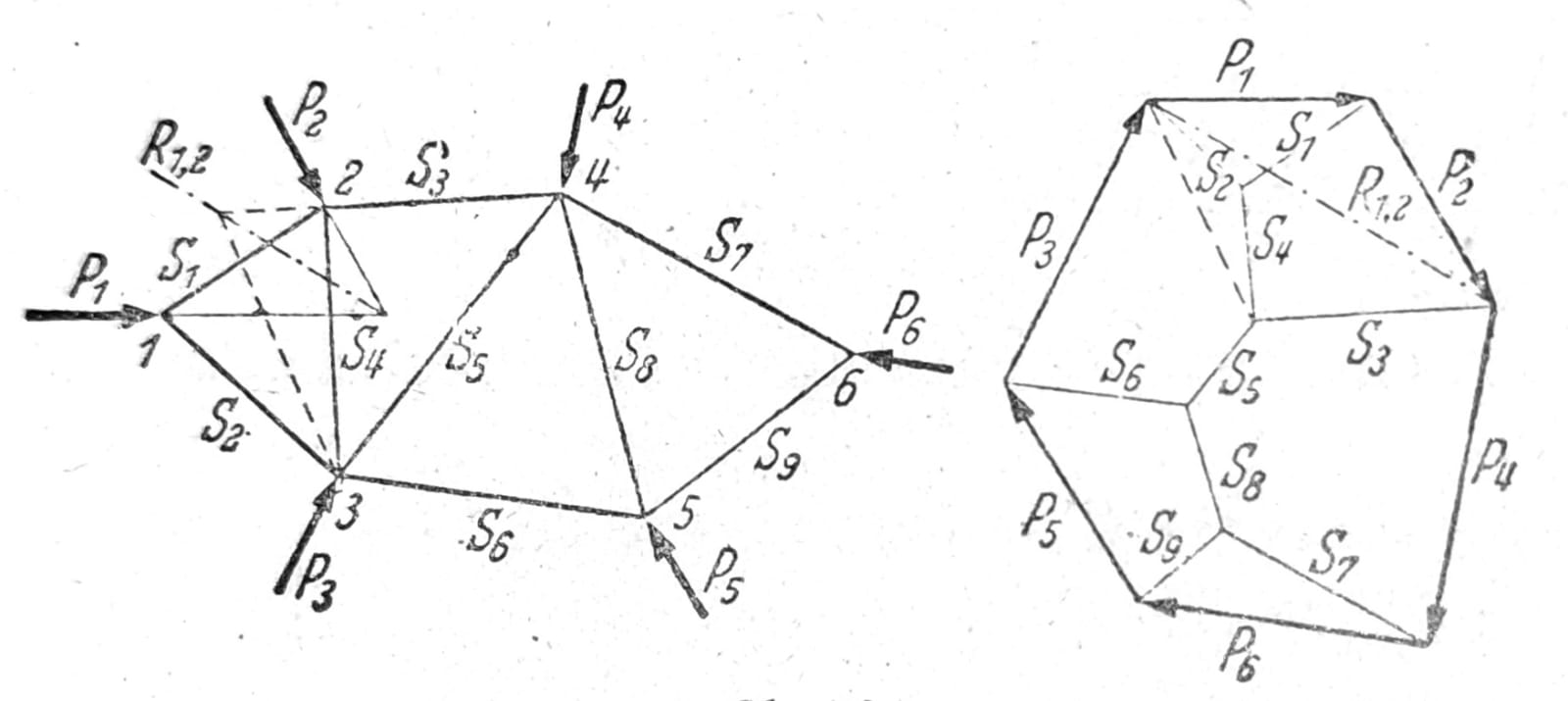
Sl. 16
Pri analitičkom rešenju zadatka za postavljanje jednačina sa po jednom nepoznatom najveći značaj ima Ritter-ov postupak. Rešetka se preseče tako da su presekom pogođena tri štapa. Sile u presečnim štapovima se na svakki deo rešetke nanesu kao sile zatezanja, od čvora ka preseku. Za svaki deo rešetke važe uslovi ravnoteže. Presek dva i dva presečna štapa je momentna tačka pri određivanju sile u trećem štapu (Ritter-ova tačka). Ako je ri odstojanje sile Si od momentne tačke i, a Mi moment aktivnih sila i reakcija oslonaca u odnosu na tačku i, tada je sila u štapu data izrazom
Si = ± Mi/ri
Sl. 17
Sl. 18
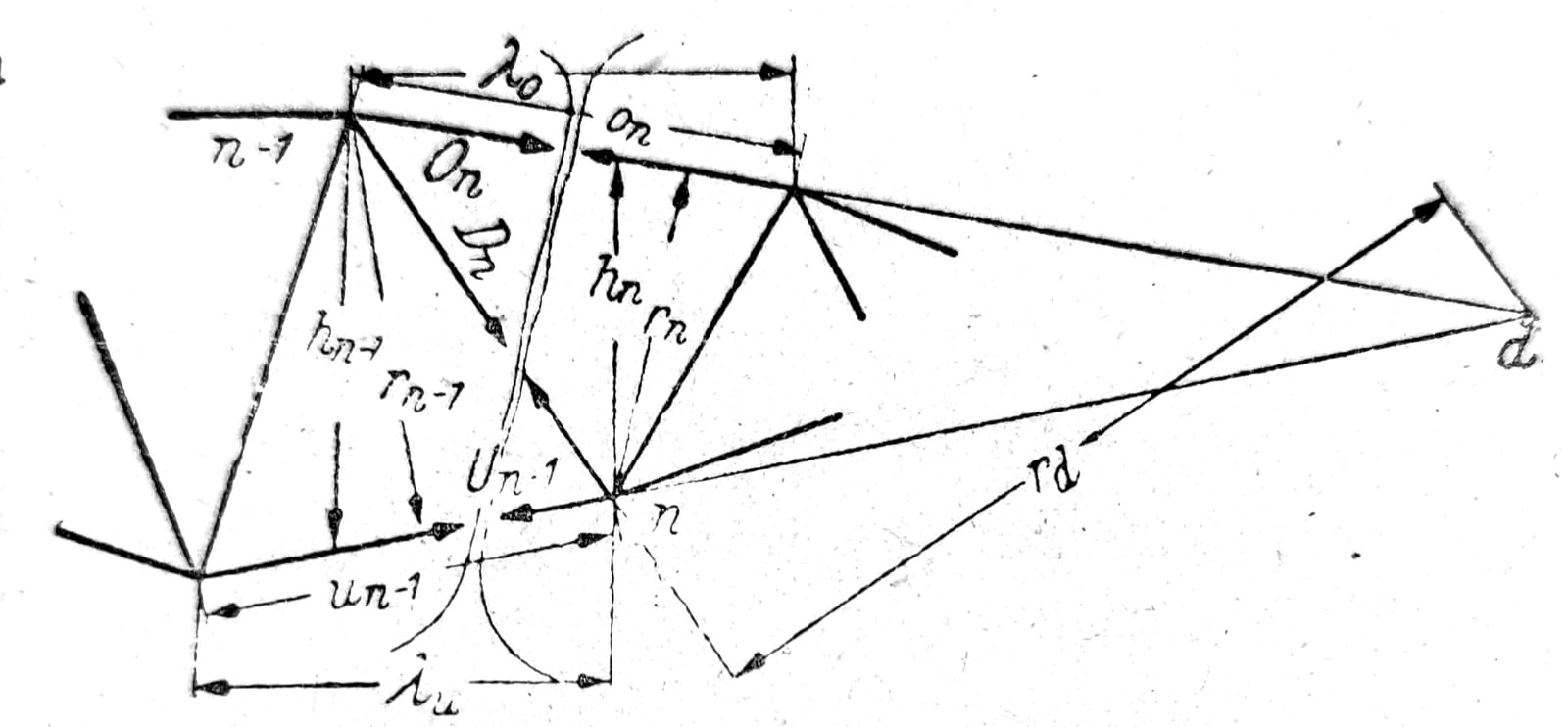
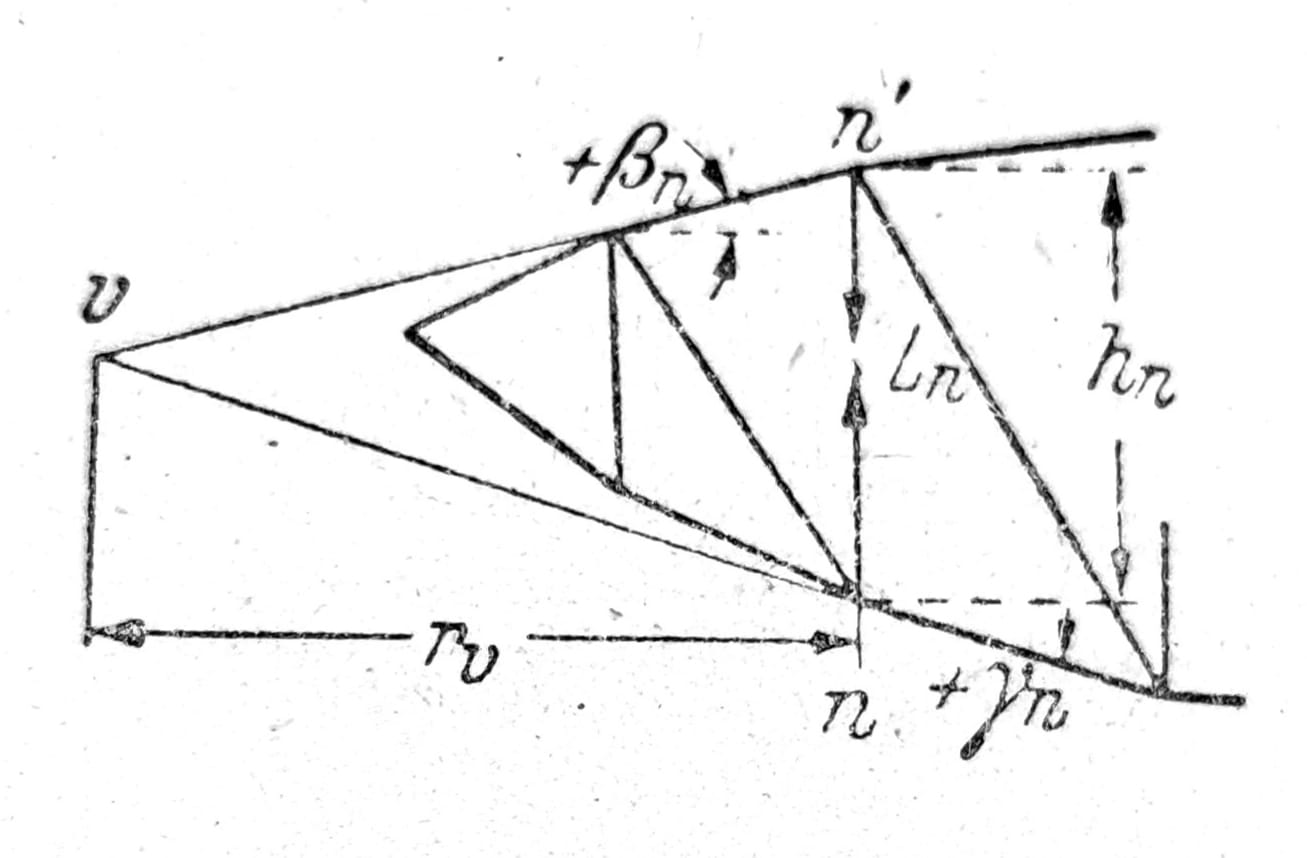
Prema sl. 17 i 18 sile u presečnim štapovima su:
On = -Mn/rn; Un-1 = Mn-1/rn-1;
Dn = Md/rd; Ln = Mv/rv.
Kada grafička konstrukcija ne daje dovoljnu tačnost, položaji momentnih tačaka d i v i odstojanja rd i rv moraju se sračunati. Za proračun sila D i L pogodniji su sledeći izrazi u kojima se kao momentne tačke pojavljuju samo karakteristične tačke rešetke, (sl. 19, 18):
D = (Mu/hu – M(o)/ho) * (d/λd), (35)
Ln = ± Ql ± (Mn tgβn + M’n tgγn)/hn.
Kod rešetki sa paralelnim pojasevima sile D i L mogu se dobiti neposredno iz transverzalne sile:
D = Q/sinφ; L=±Q
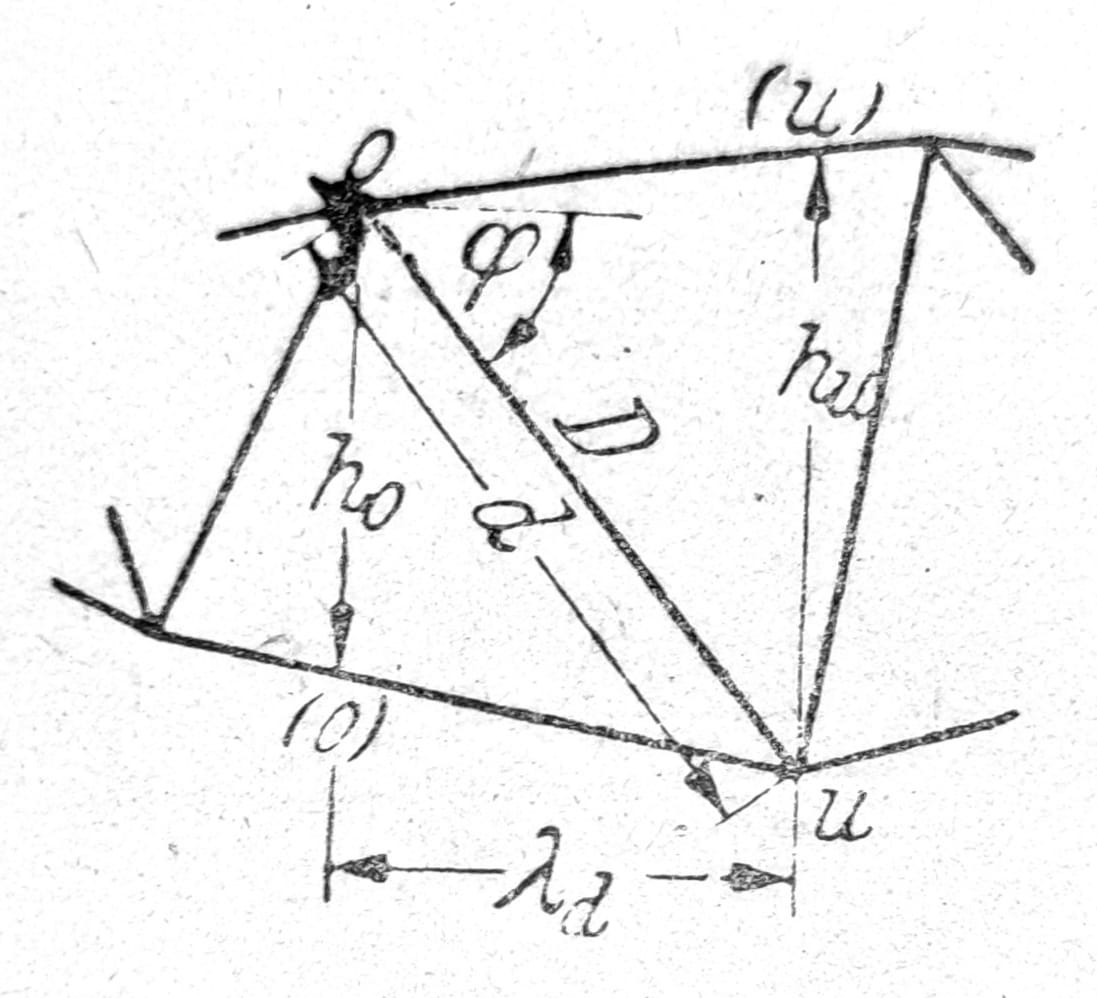
Sl. 19
Pokretno opterećenje. Uticajne linije.
Ako je nosač opterećen pokretnim opterećenjem, koncentrisanim silama na stalnom međusobnom razmaku, tada ispitivanja treba sprovesti na najnepovoljnije položaje opterećenja. Za prostu gredu na dva oslonca najveća trasverzalna sila Qmax može se dobiti pomoću A-poligona, a najveći moment savijanja Mmax pomoću verižnog poligona za sistem sila pod kojim se nosač pomera.
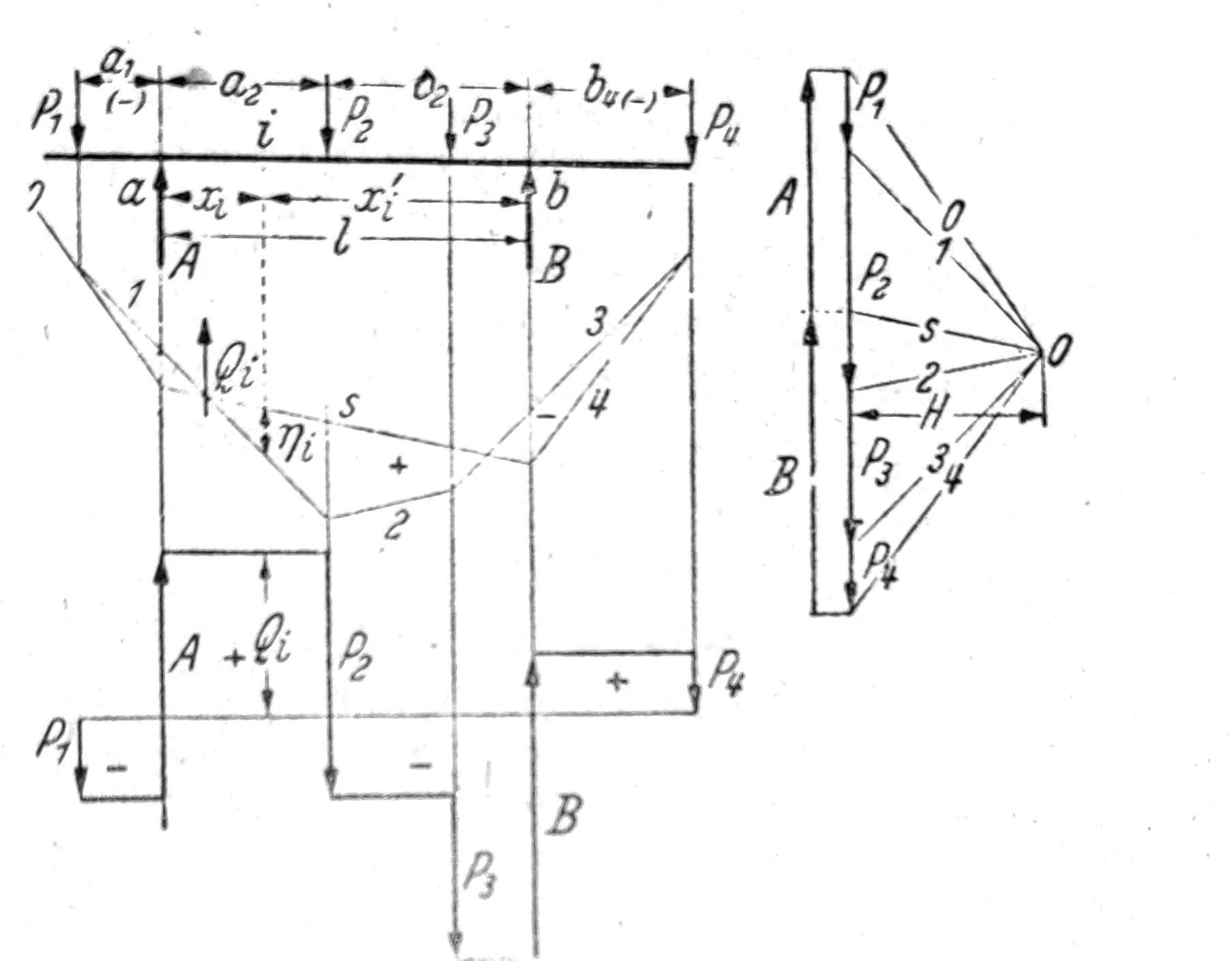
Pri određivanju uticajne linije za jednu statičku ili geometrijsku veličinu, a za teret Pm=1 koji se kreće po opterećenom pojasu nosača, za svaki položaj opterećenja m nanosi se ispod sile, od jedne nulte linije, sračunata vrednost ηm tražene veličine. Linija koja spaja krajnje tačke ovih ordinata je uticajna linija. Uticajne linije za moment savijanja Mi i transverzalnu silu Qi na mestu i grede oslonjene u tačkama a i b su prave ga i gb čiji su odsečci na vertikalama oslonaca aa’ = xi (=M’i za A=1) i bb’ = x’i (=M’’i za B=1) (sl. 20). Uticajna linija za silu A data je pravom gb, čija je ordinata na vertikali osloca a aa’=1.
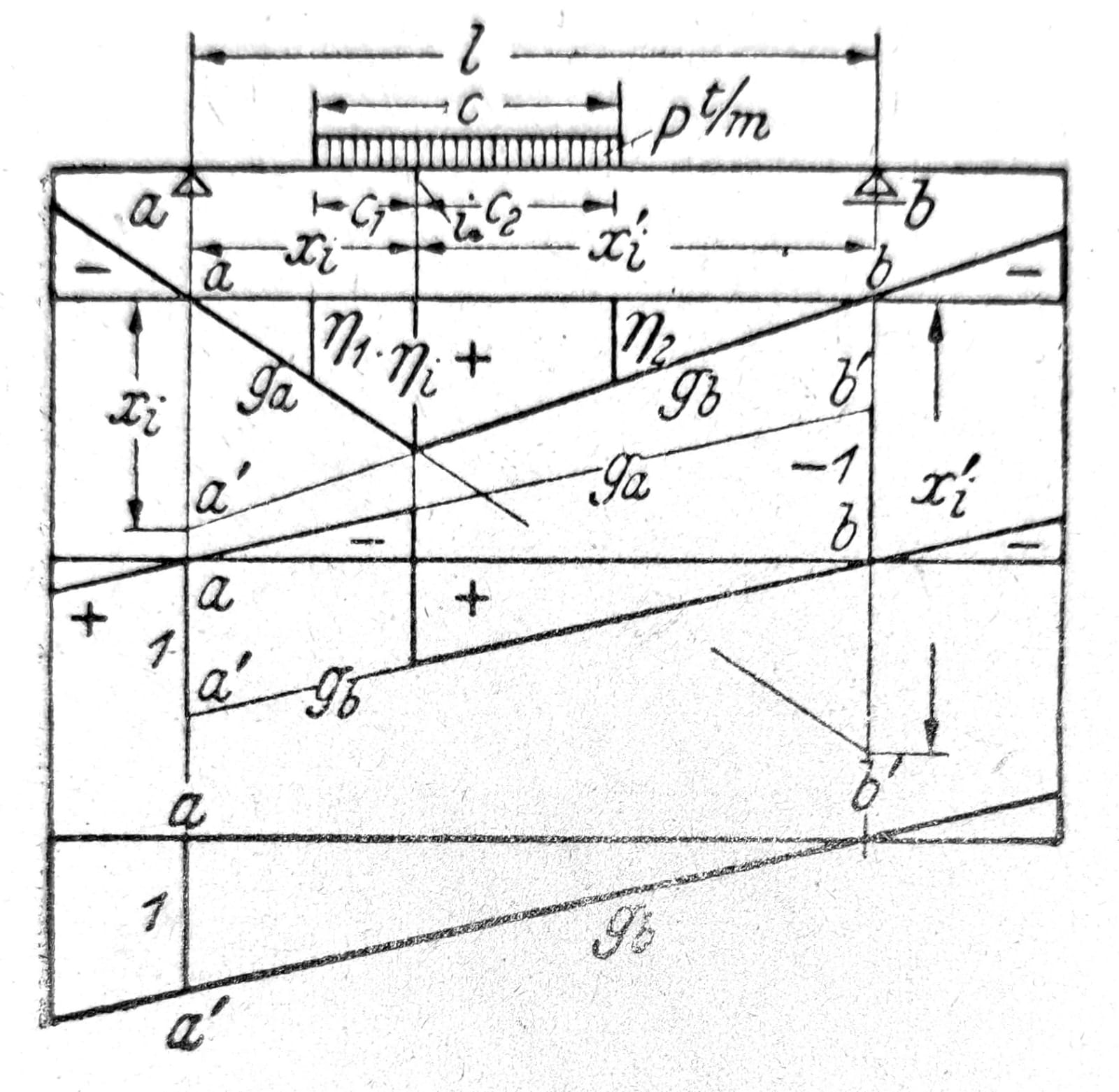
Sl. 20
Uticajna linija za svaku statičku veličinu statički određenog nosača sastoji se od pravih linija koje odgovaraju krutim pločama prinudnog kinematičkog lanca nastalog isključenjem tražene veličine. Prave se seku na vertikalama kroz momentne tačke, odn. kroz tačke u kojima su ploče zglobno vezane. Površina ograničena nultom linijom, uticajnom linijom i dvema ordinatama naziva se uticajna površina. Razdelnica (nulta tačka uticajne linije) deli pozitivne i negativne delove uticajne površine.
Kako ηm predstavlja uticaj pokretne sile Pm=1 na traženu veličinu Z, to je Pmηm uticaj sile Pm, dok sistem sila P izaziva uticaj Z=∑Pη. Granične vrednosti uticaja maxZ i minZ dobiće se kada se pokretni sistem vezanih koncentrisanih sila tako postavi da se najveće sile množe sa najvećim ordinatama. Kada se najnepovoljniji položaj ne zna sa sigurnošću, mora se uticaj iz uticajne linije uporedo sračunati za različite položaje opterećenja (iterativan proces).
Za delimično jednakopodeljeno opterećenje p t/m je Z = ∫p dx η = pF, gde je F obeležena veličina merodavnog dela uticajne površine. Kod delimičnog opterećenja ograničene dužine c i pravolinijskog oblika uticajne linije (sl. 58) teret treba postaviti tako da je η1 = η2 (c1 = cxi/l; c2 = cx’i/l), pa se dobija Z = pc (ηi + η1)/2. Pri posrednom prenošenju opterećenja, uticajna linija se između ordinata ηn i ηn+1 menja pravolinijski, sl. 21.
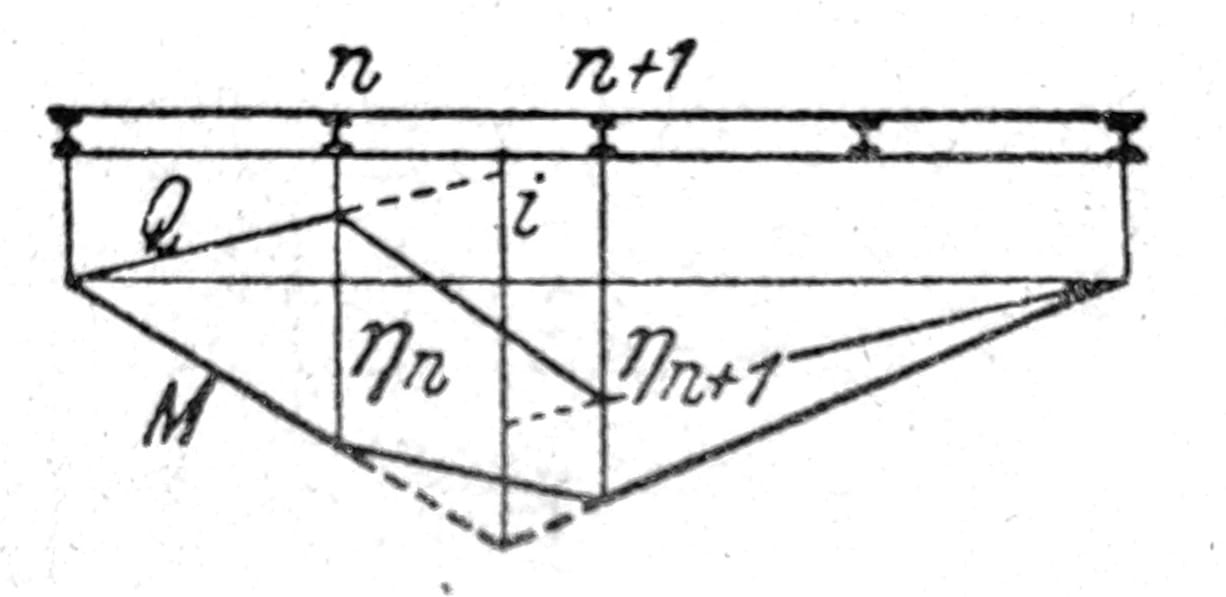
Sl. 21