Statika konstrukcija – Primena statički određenih sistema

Prosta greda

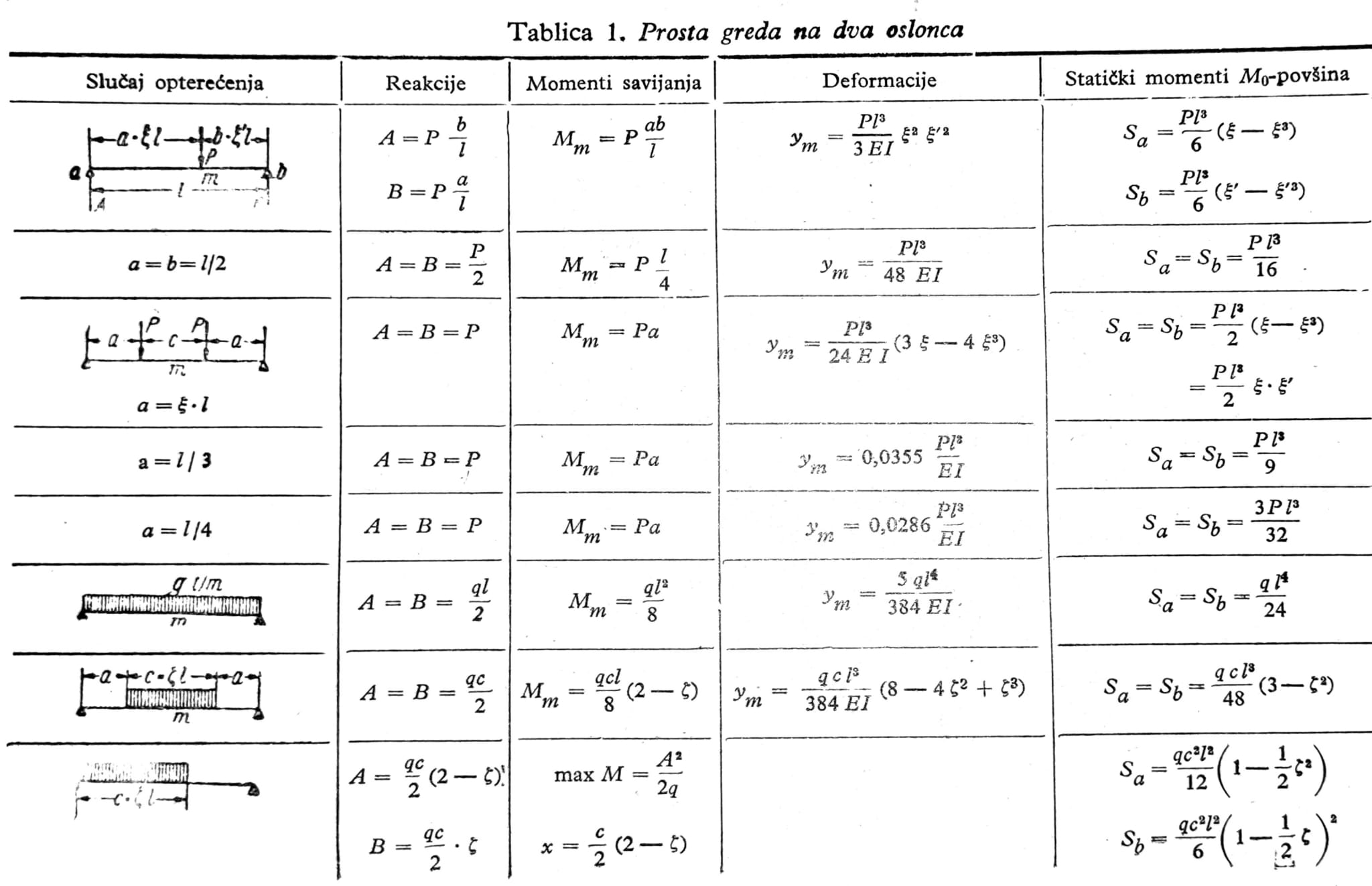
Reakcije oslonaca, momenti savijanja, deformacije i statički momenti M₀-površina za neke slučajeve opterećenja koji se često pojavljuju dati su u tablici 1.

Stalno opterećenje koncentrisanim silama. Pri simetričnom opterećenju (sl. 1) račun je najlakše sprovesti putem dve adicione kolone u obliku tablice. Na osnovu veze između opterećenja, transverzalne sile i momenta

Q_n = Q_n+1 + P_n i M_n+1/λ = M_n/λ + Q_n+1

određuje se najpre transverzalna sila u polju n polazeći od transverzalne sile u sredini grede a zatim momenti savijanja u pojedinim tačkama polazeći od vrednosti M_i/λ.

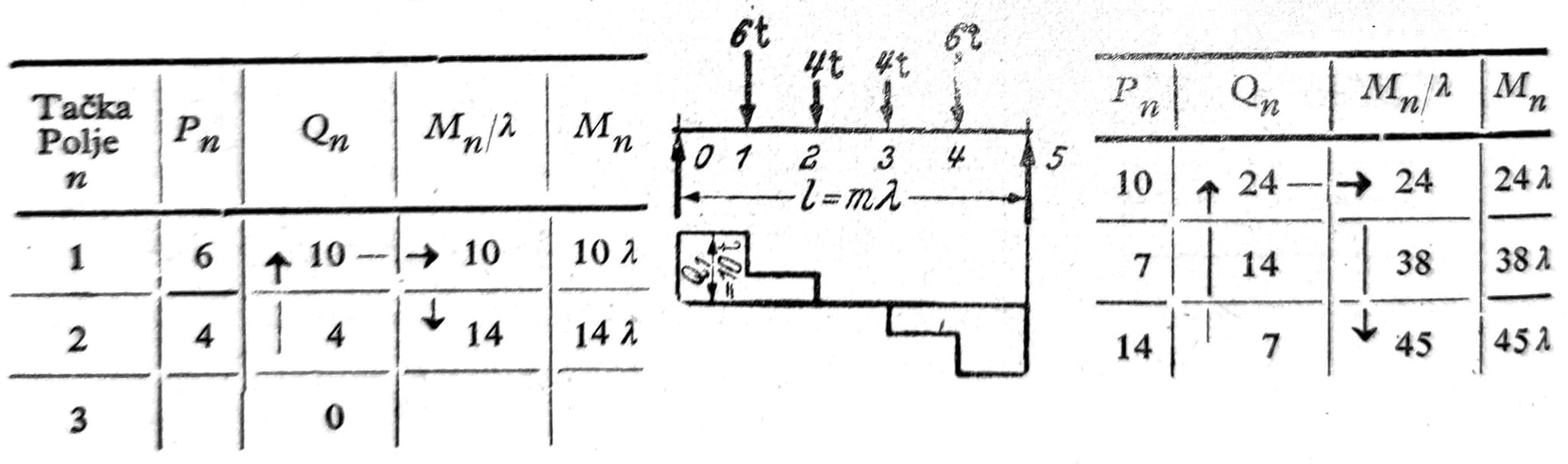
Sl. 1 sa pomoćnim tablicama

Kada je opterećenje nesimetrično, a razmaci sila jednaki, za proračun su pogodne sledeće tablice (sl. 2). Svako nesimetrično opterećenje može se prema sl. 3 zameniti jednim antimetričnim opterećenjem, što je pri proračunu često vrlo korisno. Umesto sila P_i i P’_i pri simetričnom slučaju opterećenja pojavljuju se sile (P_i+P’_i)/2 u tačkama i i i’, a pri antimetričnom slučaju opterećenja pojavljuje se sila (P_i-P’_i)/2 u tački i i sila -(P_i-P’_i)/2 u tački i’. Kada su pri antimetričnom opterećenju određene reakcije oslonaca, transverzalne sile i momenti savijanja mogu se takođe odrediti u tablici.

Sl. 2

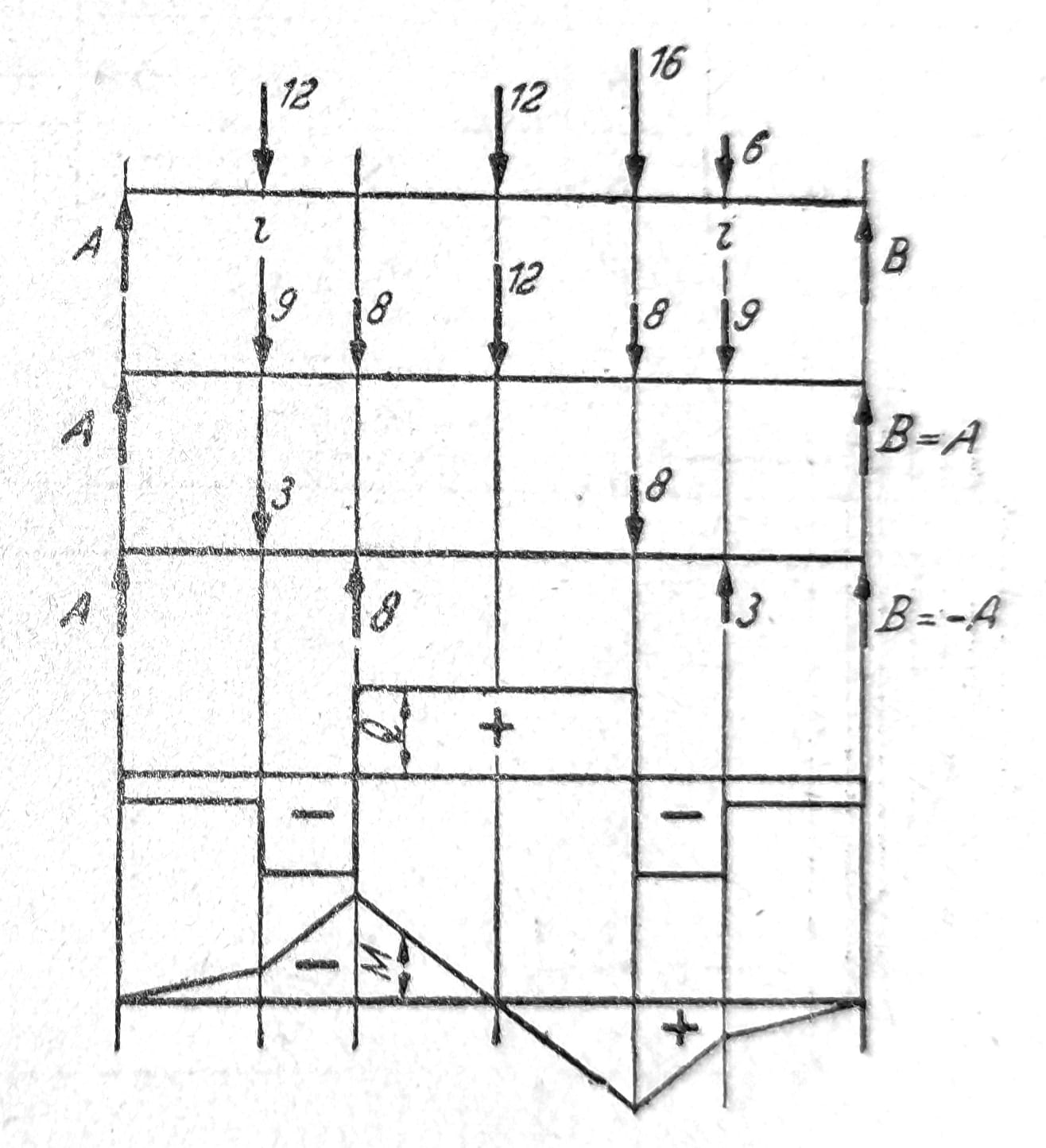
Sl. 3

Pokretno opterećenje. Moment savijanja na mestu i grafički se dobija pomoću poligona sila i verižnog poligona za dato opterećenje. Verižni poligon može se nacrtati kao što je pokazano na sl. 4. Da bi se odredio najnepovoljniji položaj opterećenja za moment na mesu i nosač se pomera pod opterećenjem (sl. 5) dok se ne odredi vradnost max η_i iz koje se dobija maxM_i = H * maxη_i. Najveća transverzalna sila u tački i dobija se kada se opterećenje pomeri tako da prva sila dođe do tačke i. Ona se može dobiti iz poligona sila na sl. 6: maxO_i = 1/l * ∑P_ib_i. A-poligon je verižni poligon sa odstojanjem pola H = l, nacrtan za pokretan sistem koncentrisanih sila kada se prva sila nalazi nad osloncem b.

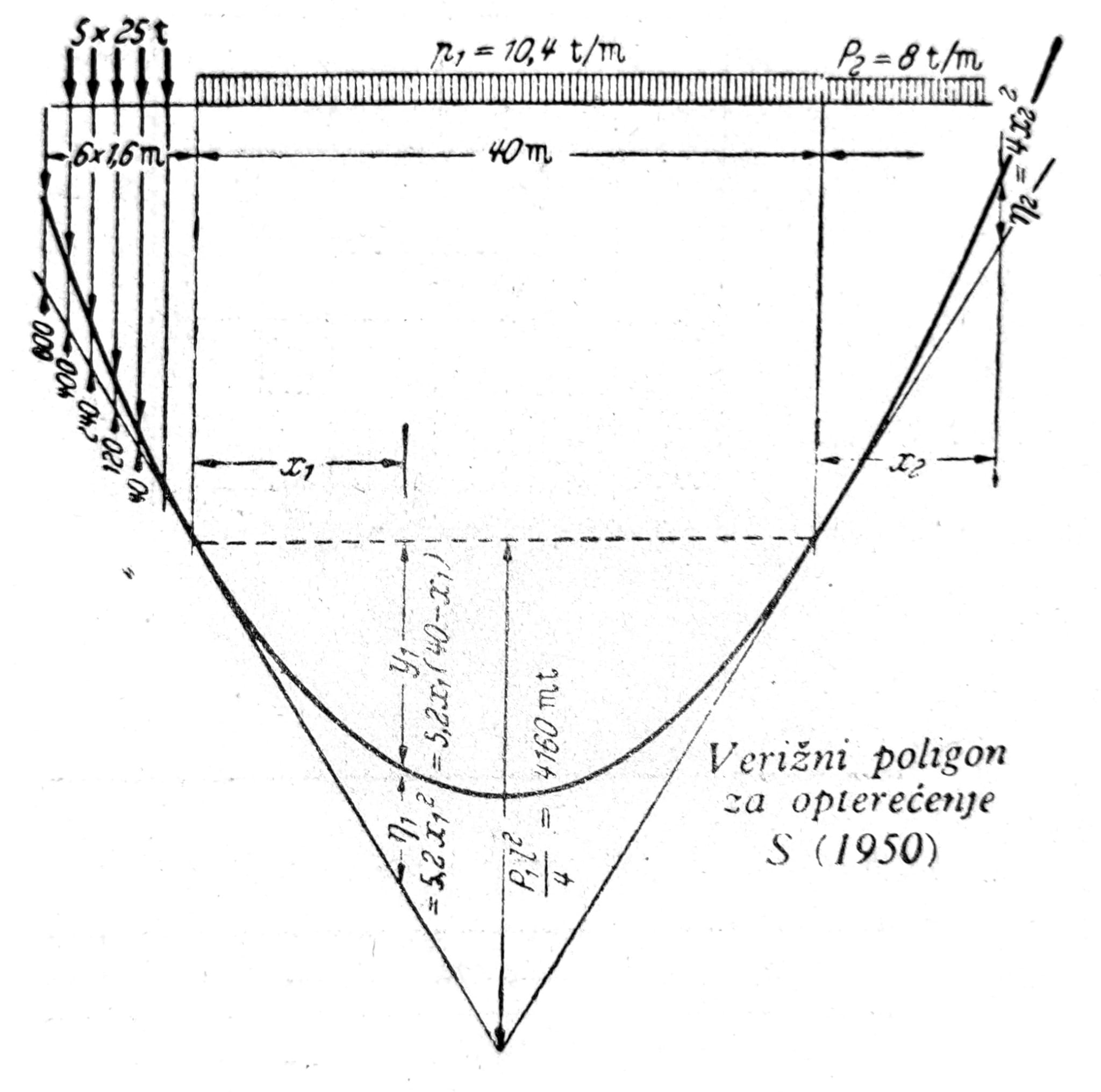
Sl. 4

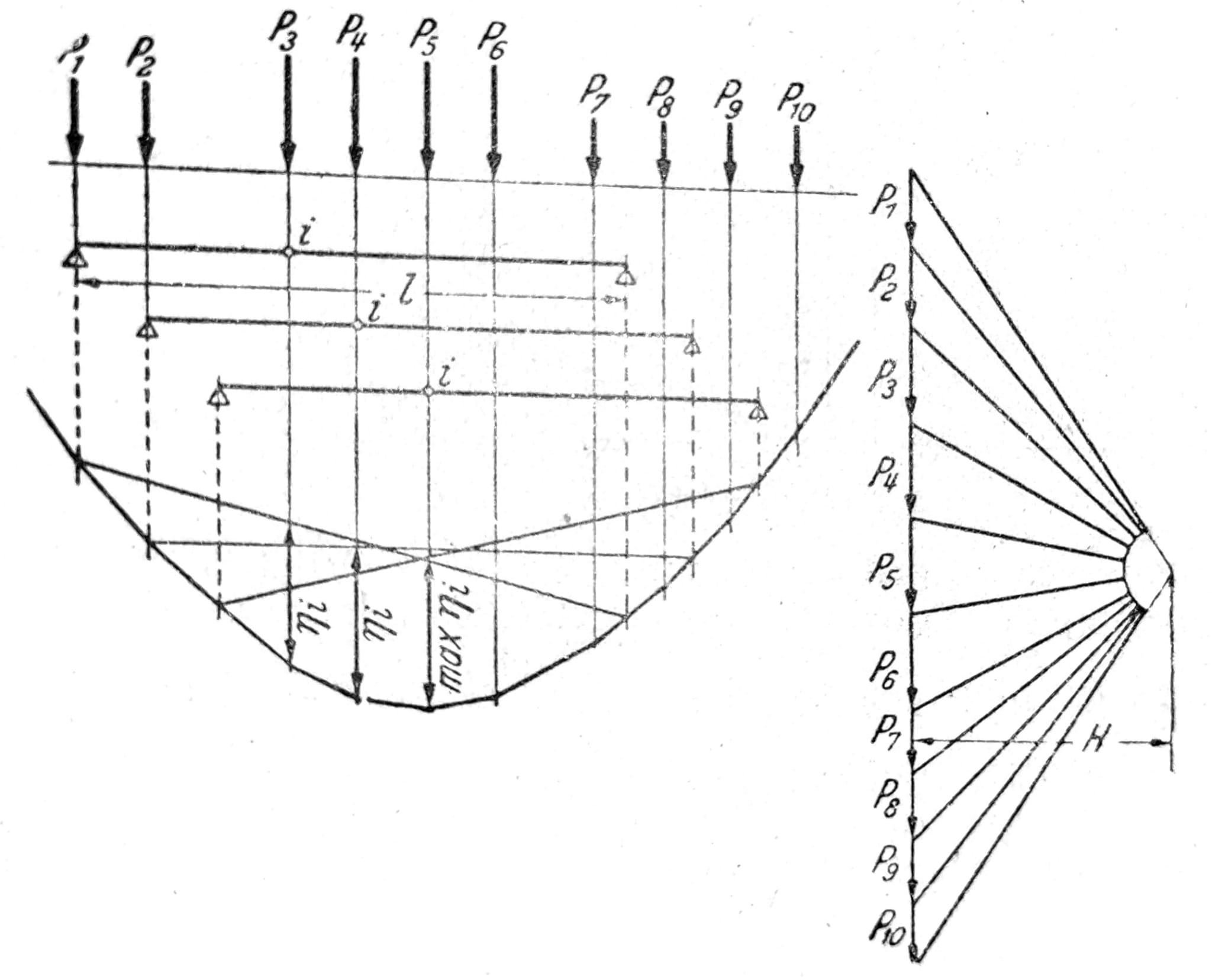
Sl. 5

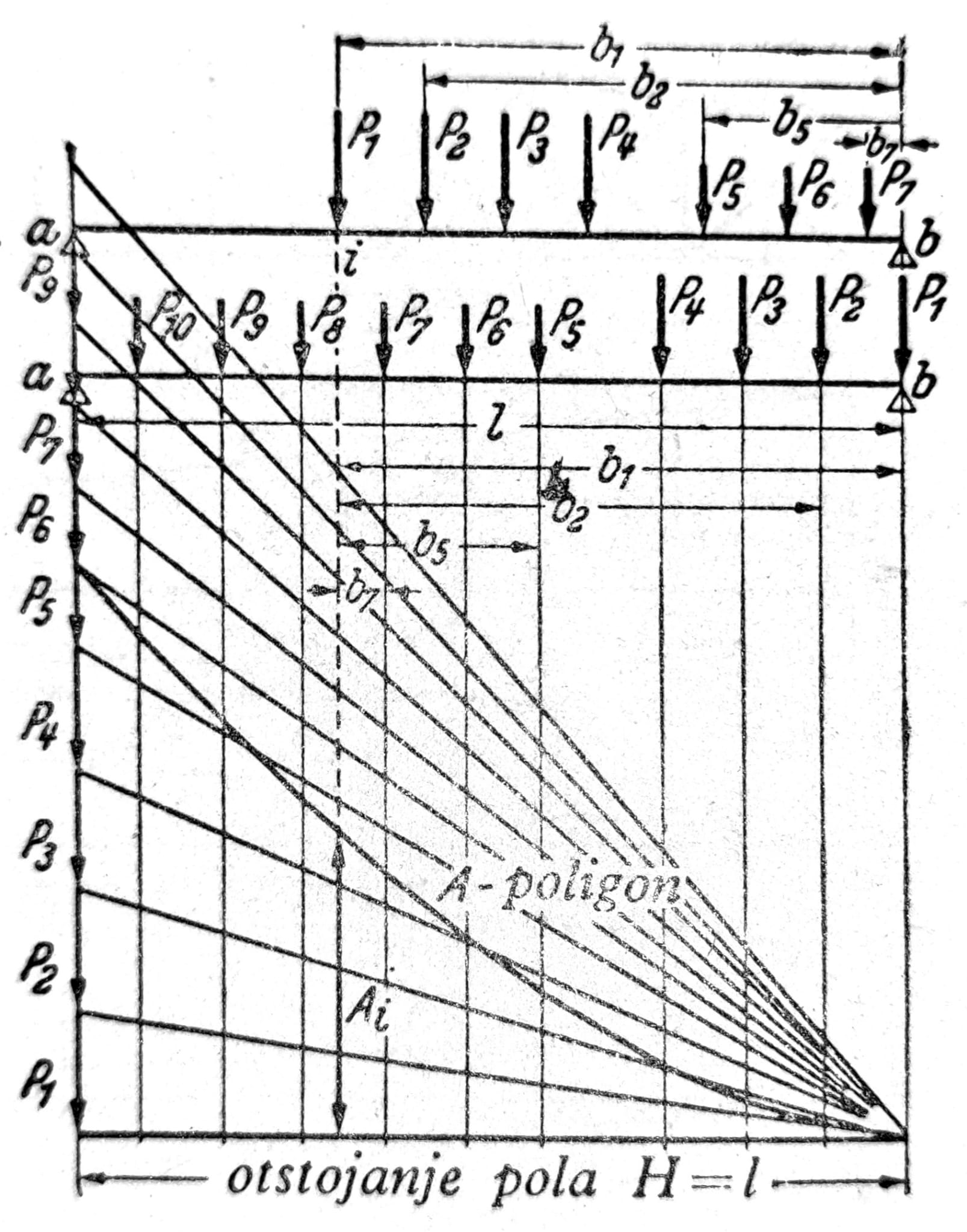
Sl. 6

 

Nosač sa zglobovima

Stalno opterećenje. Najpre se određuju reakcije oslonaca i sile u zglobovima iz uslova ravnoteže i uslova za zglobove. Zatim se momenti savijanja i transverzalne sile za pojedine ploče nosača mogu odrediti kao kod prostih greda, odn. greda sa prepustima. Sl. 7 pokazuje rezultat za opterećenje triju ploča koncentrisanim silama. Linija transverzalnih sila prelazi preko zglobova kao konstanta, a momentna linija bez preloma, ukoliko u zglobu ne deluje koncentrisana sila.

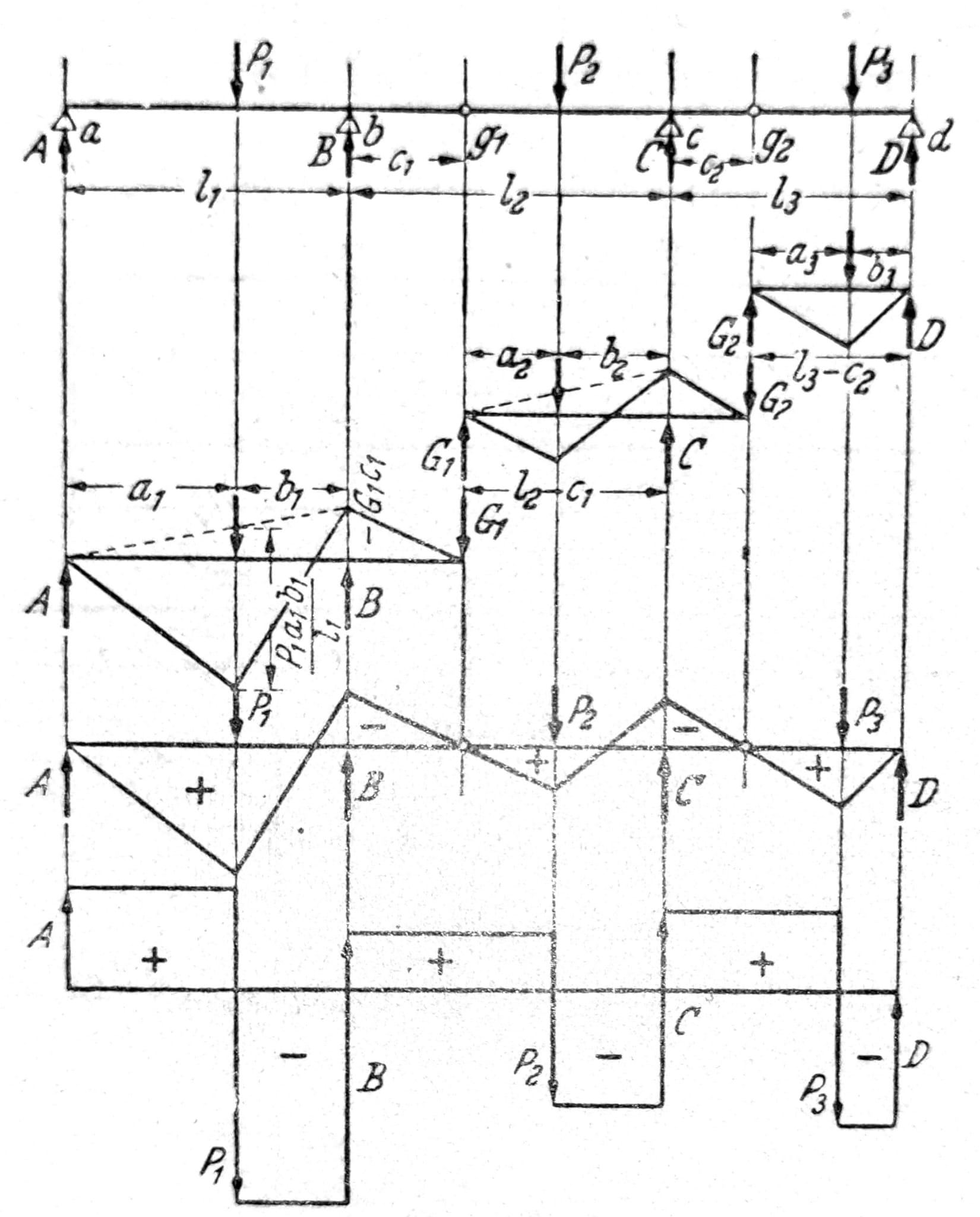
Sl. 7

Za jednakopodeljeno opterećenje po čitavom nosaču dobijaju se poneka, prema odnosima raspona i položaju zglobova, velike razlike između momenata nad osloncima i maksimalnih momenata u poljima, sl. 8. Ako se kod nosača sa zglobovima sa više od dva otvora (sl. 9) i sa jednakim rasponima l srednjih polja izabere raspon krajnjih polja l₁=0,8535l i položaj zglobova c=0,1465l, tada se pri jednakopodeljenom opterećenju dobija da su granične vrednosti momenata nad osloncima i u poljima međusobno jednake, M=0,0625gl². Ako i krajnja polja imaju raspon l, tada je za njih maxM=0,0957gl².

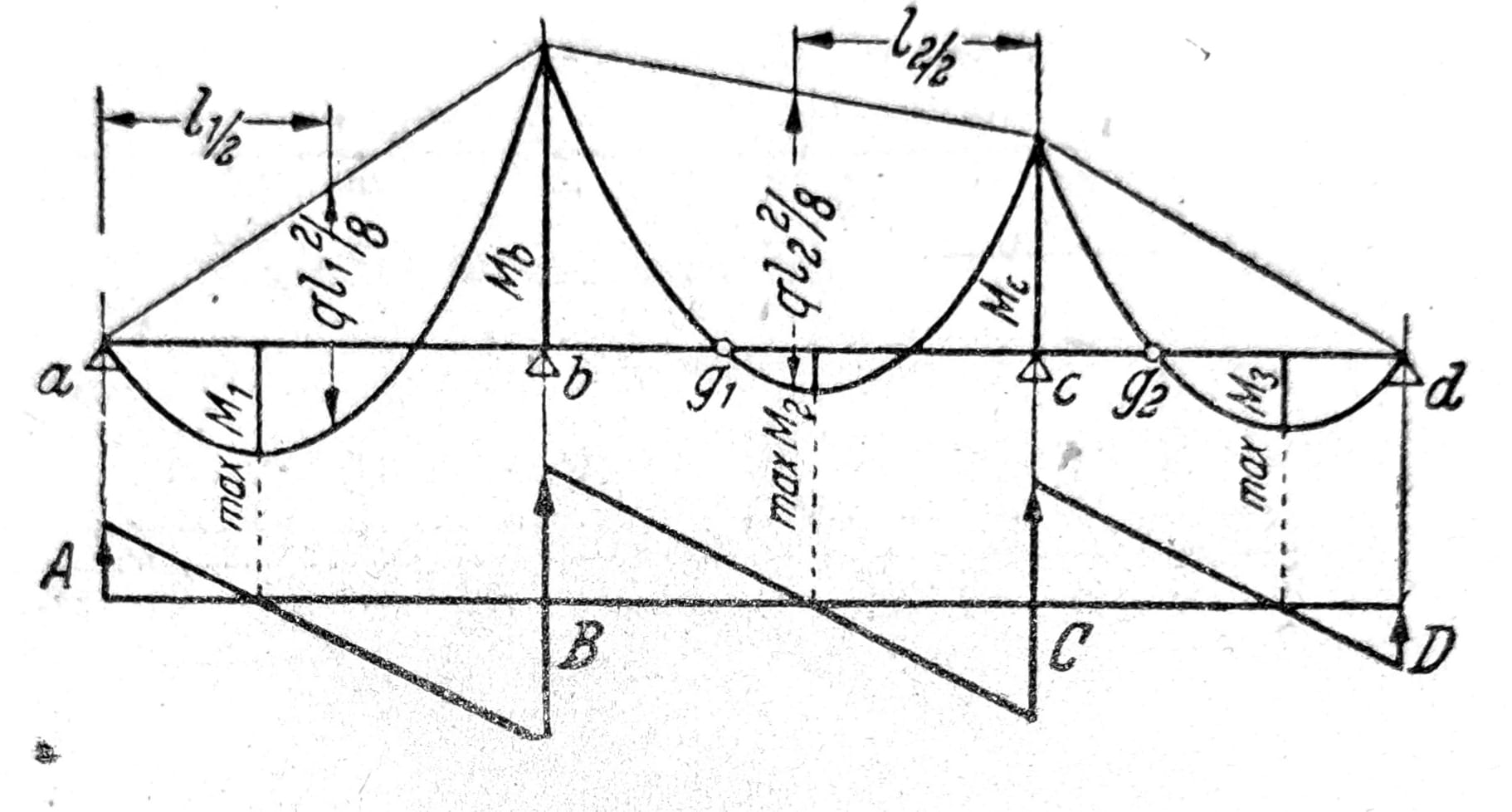
Sl. 8

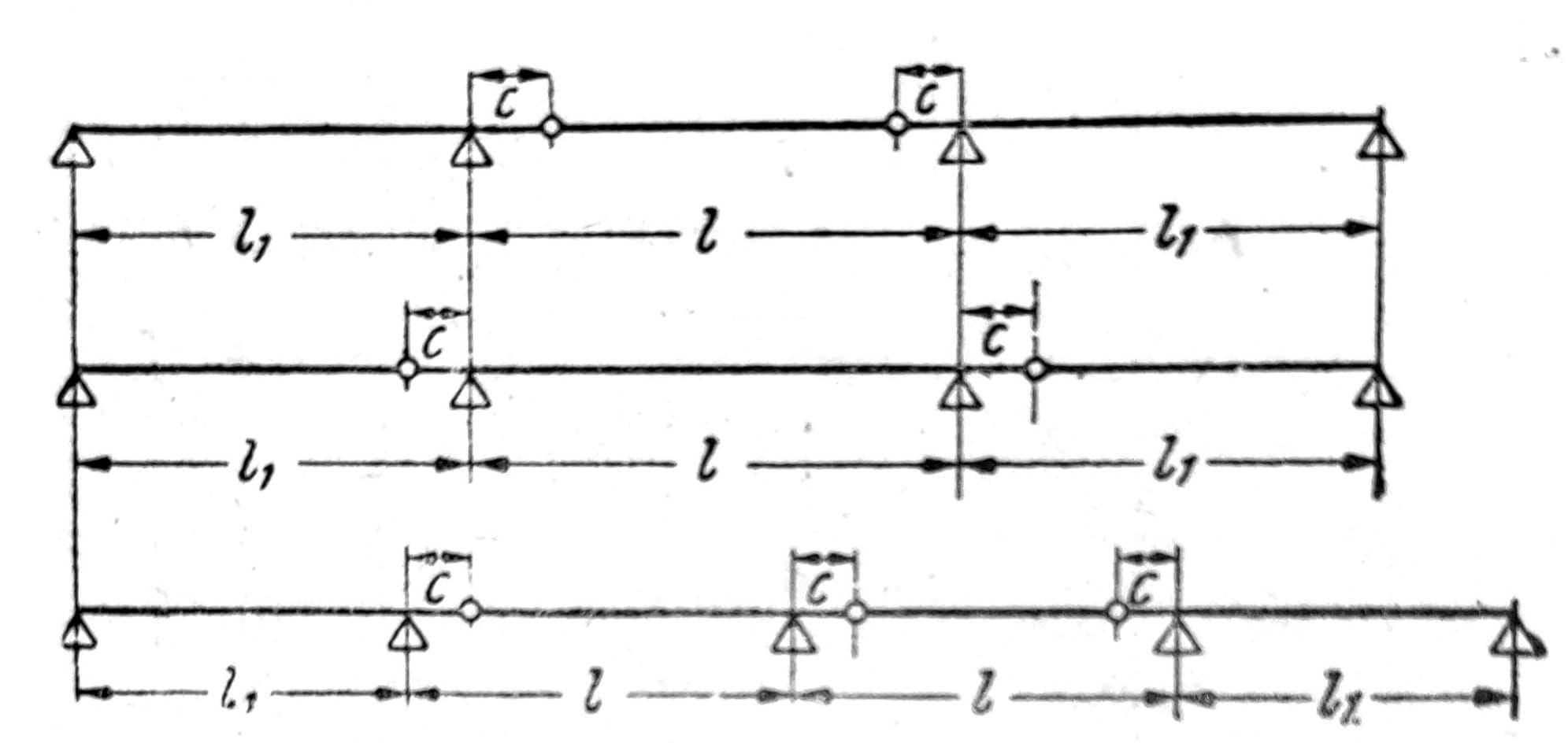
Sl. 9

Uticajne linije. Prema sl. 10 uticajne linije za M_i i Q_i između tačaka a i b iste su kao uticajne linije proste grede. Dalji tok uticajne linije određen je položajem oslonaca i zglobova koji predstavljaju glavne polove i međupolove kinematičkog lanca nastalog uklanjanjem statičke veličine u tački i. Na sličan način određuju se uticajne linije za M_r i Q_r polazeći od grede oslonjene u tačkama g₁ i c. Opterećenje grede sa prepustom na delu ag₁ nema uticaja na momente i transverzalne sile u tački r. Uticajne linije za momente i transverzalne sile u tačkama prepusta (k i v) najlakše se dobijaju kada se odrede ordinate za položaj opterećenja u zglobu.

Sl. 10

 

Luk na tri zgloba

Pri proizvoljnom opterećenju luka na tri zgloba reakcije oslonaca mogu se odrediti grafički. Rezultanta R₁ aktivnih sila koje prema sl. 11 deluju na levu ploču mora stajati u ravnoteži sa reakcijom K_b1, čija napadna linija mora prolaziti kroz zglob g, i reakcijom K_a1. Na isti način nalaze se K_a2 i K_b2, usled R₂. Pri istovremenom dejstu R₁ i R₂ dobijaju se paralelnim pomeranjem i slaganjem sila konačne reakcije K_a i K_b i pritisak u zglobu G.

Sl. 11

Pri analitičkom rešenju proračun je zgodno sprovesti posevno za horizontalna i posebno za vertikalna opterećenja. Horizontalno opterećenje na sl. 12 izaziva reakcije

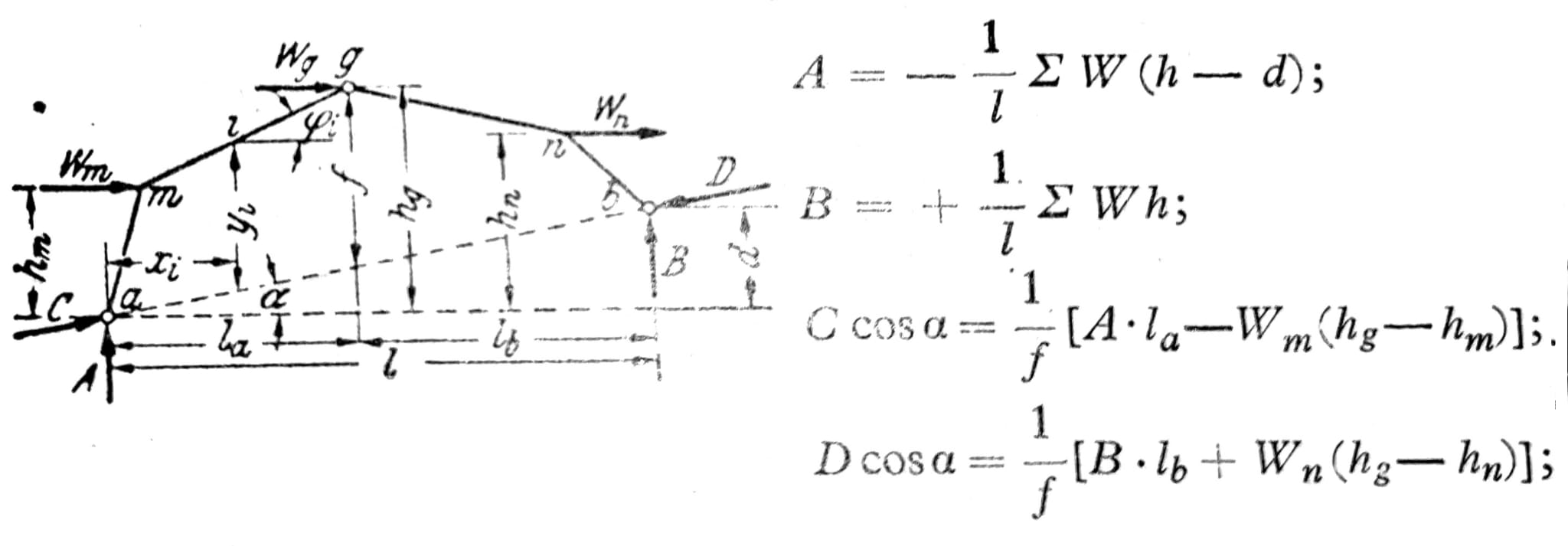
Sl. 12

gde su C i D komponente reakcija u pravcu koji spaja tačke a i b. Za kontrolu služi ∑H = C*cosa – Dcosa + ∑W = 0. Presečne sile na mestu i su:

N_i = -Asinφ_i – Ccos(φ_i-a) – W_mcosφ_i,

Q_i = +Acosφ_i – Csin(φ_i-a) – W_msinφ_i,

M_i = Ax_i – Ccosa*y_i – W_m(h_i-h_m).

Vertikalno opterećenje luka na tri zgloba na sl. 13 izaziva reakcije A₀ i B₀, koje su jednake reakcijama proste grede raspona l, i horizontalni potisak C=cosa = Dcosa = H = M_g0/f   (1), gde je M_g0 moment na prostoj gredi u preseku g. Sa vertikalnim komponentama C i D konačne vertikalne komponente reakcija su A = A₀ + Htga; B = B₀ – Htga. Ako je osovina luka kvadratna parabola, y_i = f x_i x’_i/l_a l_b, tada je za jednakopodeljeno puno opterećenje g t/m (sl. 14) M_i=0, Q_i=0.

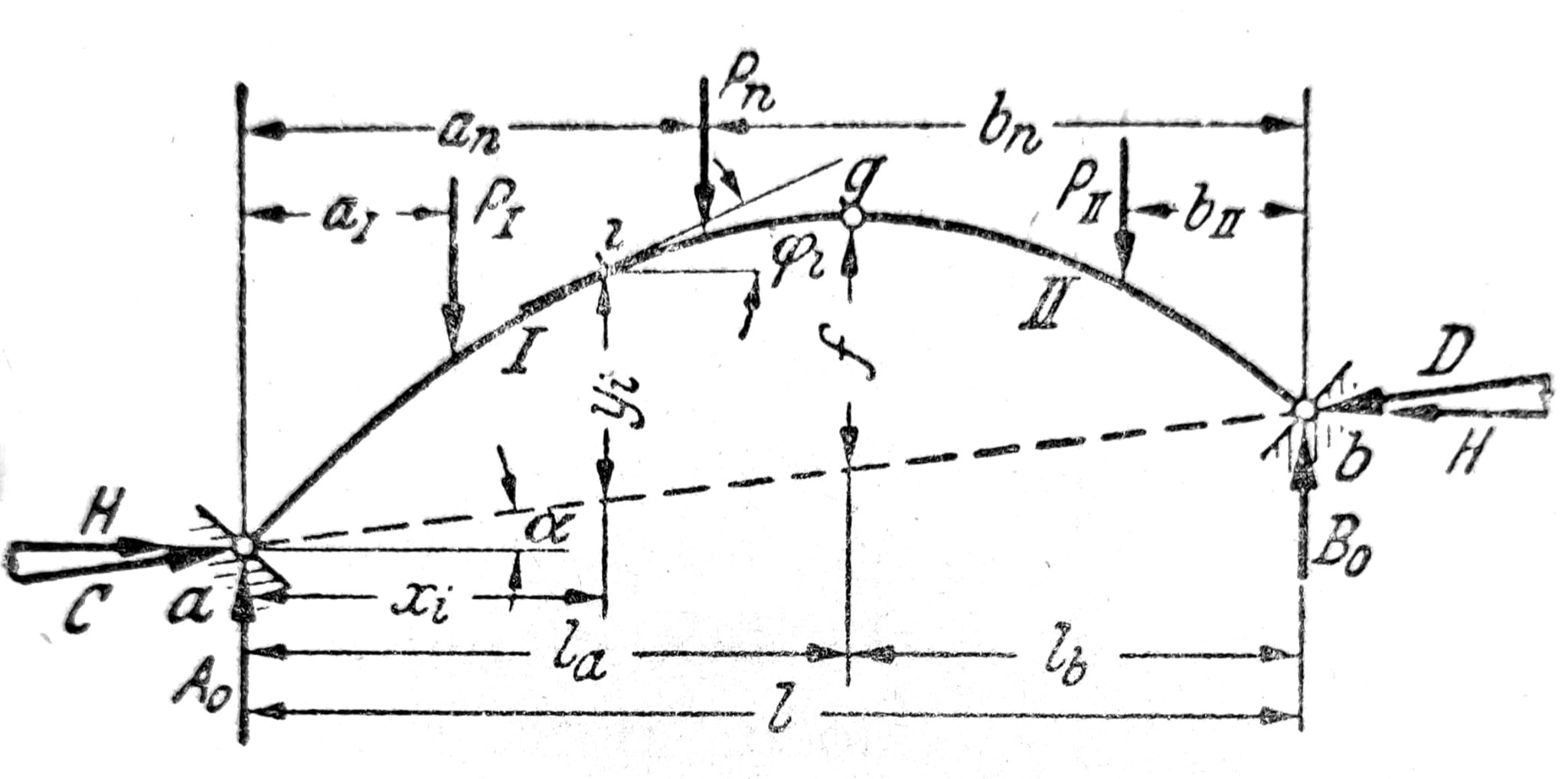
Sl. 13

Sl. 14

Uticajne linije. Uticajne linije za reakcije A₀ i B₀ iste su kao uticajne linije proste grede. Uticajna linija za horizontalan potisak H dobija se prema jednačini (1) iz uticajne linije za moment M_g0 proste grede, sl. 15. Uticajna linija za moment savijanje M_i sastoji se iz uticajnih linija sa M_i0 i H, pri čemu se poslednja množi sa -y_i. Ove dve uticajne linije superponirane su u odnosu na prabu ab’ kao nultu liniju, od koje su naneti odsečci aa’ = x_i i bb’ = -l_b y_i/f. Razlika prikazana potezom ai’g’b predstavlja konačnu uticajnu liniju za M_i. Razdelnica ili nulta tačka uticajne linije koja odgovara glavnom polu ploče ig dobija se presekom pravih ai i bg. Ona se, takođe, može koristiti za kostrukciju uticajne linije, pri čemu se uvodi prosta greda raspona a – n. Kod luka čija je osovina kvadratna parabola jednakopodeljeno opterećenje ne izaziva momente savijanja, pa ukupna površina uticajne linije mora biti jednaka nuli.

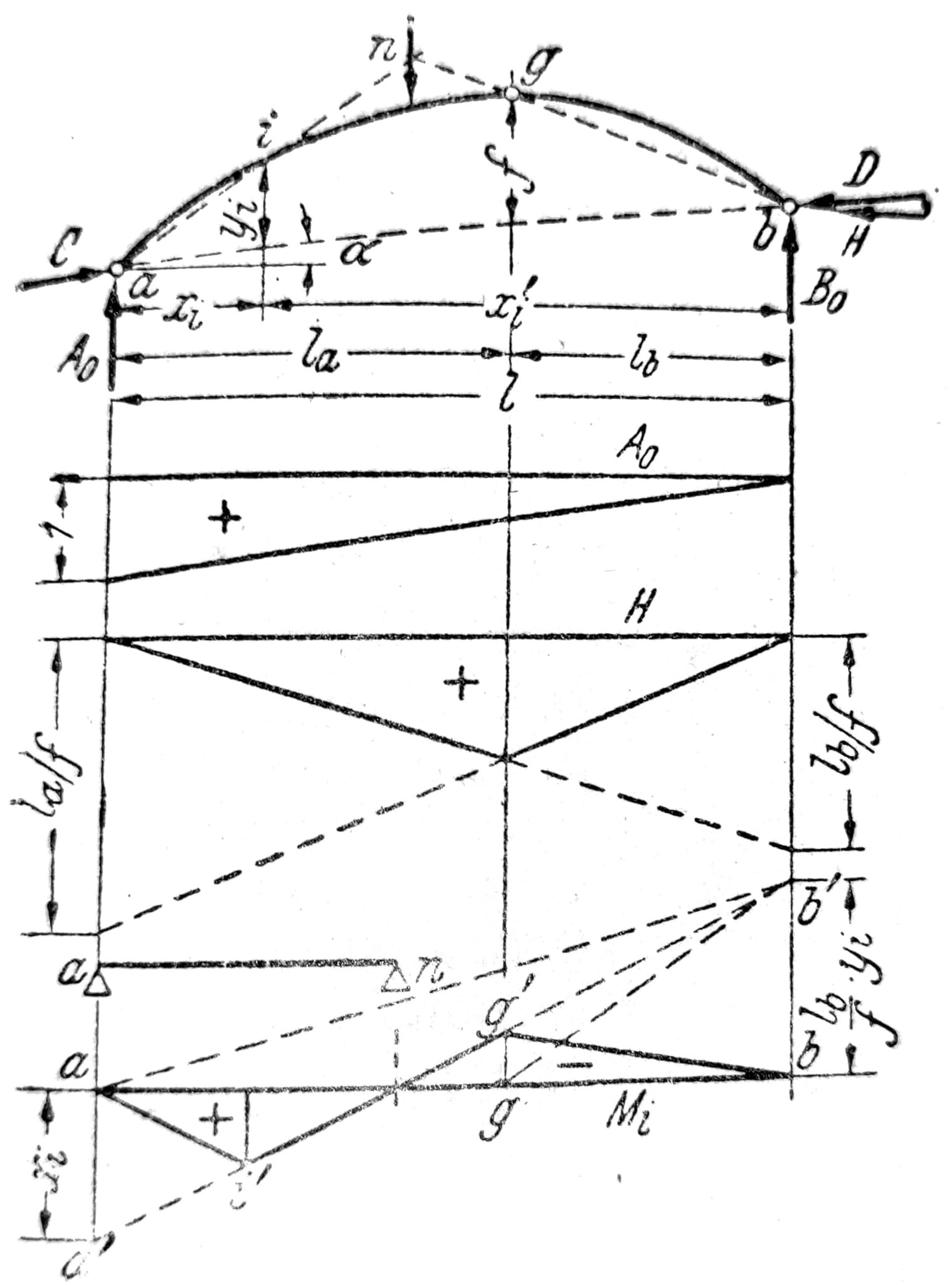
Sl. 15

Na sl. 16 dobijene su uticajne linije za Q_i i N_i odgovarajućom superpozicijom uticajnih linijja za Q_i0 i H. U odnosu na ab’ kao nultu liniju, obe uticajne linije su u ovom slučau uticajne linije proste grede. Za konstrukciju ili kontrolu uticajnih linija mogu ovde poslužiti preseci n_Q i n_N prave bg i prave provučene kroz a paralelno, odn. normalno na tangentu koja sa horizontalom zaklapa ugao φ_i. Kod paraboličnog luka na tri zgloba ukupna površina uticajne linije za transverzalnu silu mora biti jednaka nuli.

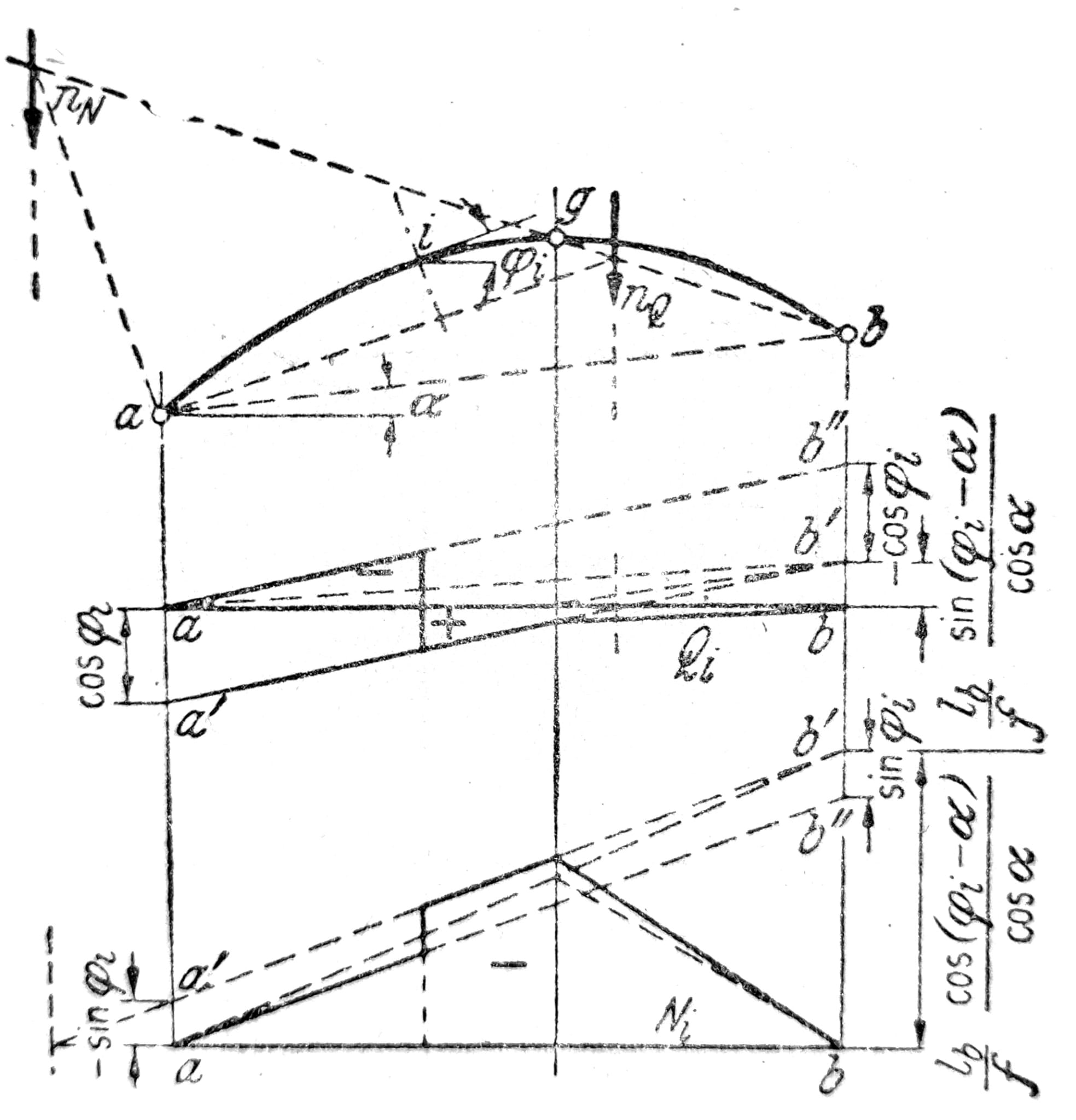
Sl. 16

 

Luk ukrućen gredom i viseći nosač

Verikalno opterećenje. Vertikalne reakcije pri vertikalnom opterećenju krutih ploča statički određenih lučnih nosača ukrućenih gredom, visećih nosača i luka na tri zgloba i zategom na sl. 17 a do f dobijaju se iz jednačina A₀ = 1/l * ∑P_nb_n i B₀ = 1/l * ∑P_na_n kada se za sisteme a i d stavi A₀ = A+K’’_l, B₀ = B+K’’_r a za ostale sisteme A = A₀, B=B₀. Reakcije A i B za sisteme a i d određuju se tada iz:

A = A₀ – K’’_l = A₀ – H(tga_l-tgδ)

B = B₀ – K’’_r = B₀ – H(tga_r+tgδ)

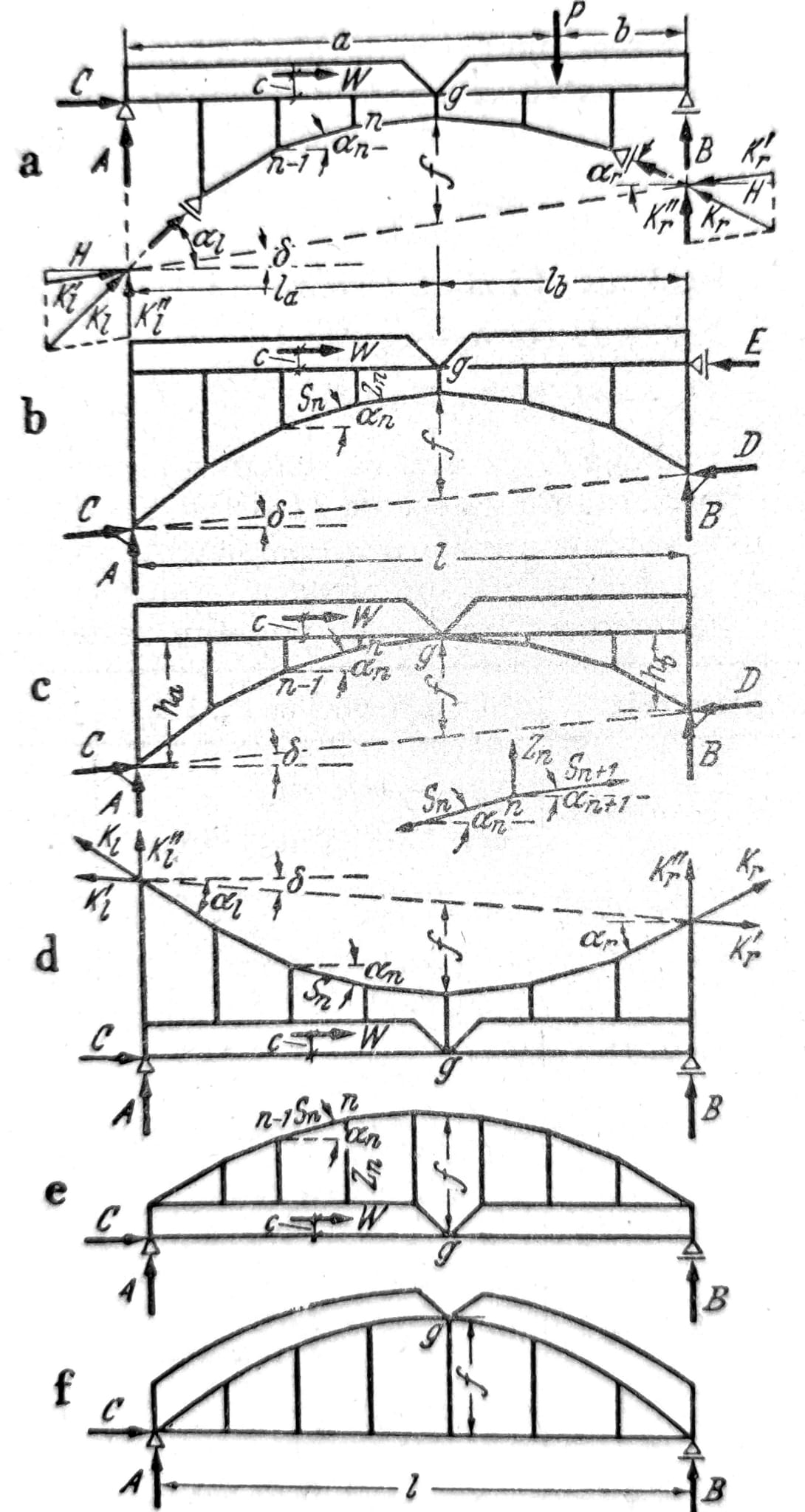
Sl. 17

Za sisteme a, d, e i f je horizontalna reakcija C=0, a za sistem b je E=0. Horizontalni potisak, odn. horizontalno zatezanje H sistema a do d, horizontalna komponenta sile u luku sistema e i sila u zatezi sistema f određuju se na osnovu jednačine (1). Sledeća tablica sadrži pregled reakcija oslonaca i sila u štapovina S_n i Z_n za pojedine sisteme.

Horizontalno opterećenje. Ako na ploče deluje horizontalna sila W na odstojanju c od zgloba g (sl. 17 a do e) reakcije oslonaca koje ona izaziva su:

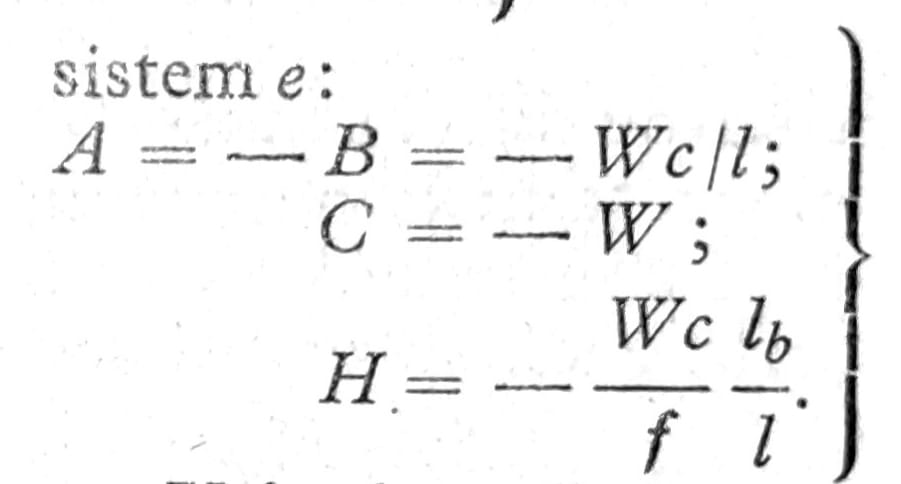
Uticajne linije. Uticajne linije za presečne sile dobijaju se na osnovu sličnosti u ponašanju ovih sistema i običnog luka na tri zgloba. Za štapasti luk sa gredom za ugrućenje ispod luka (Langerova greda) na sl. 18 prikazane su uticajne linije za U₂, D₄ i L₄. Sila u štapu U₂ dobija se iz momenta za tačku 2 gornjeg pojasa: U₂ = M₂/h. Iz uslova ∑V=0 dobija se D₄ = Q₄₀/sinφ – M_g0/f tga₄/sinφ. Takođe iz uslova ∑V=0 sledi (opterećenje na donjem pojasu) L₄ = -Q₅₀ + M_g0/f * tga₄.

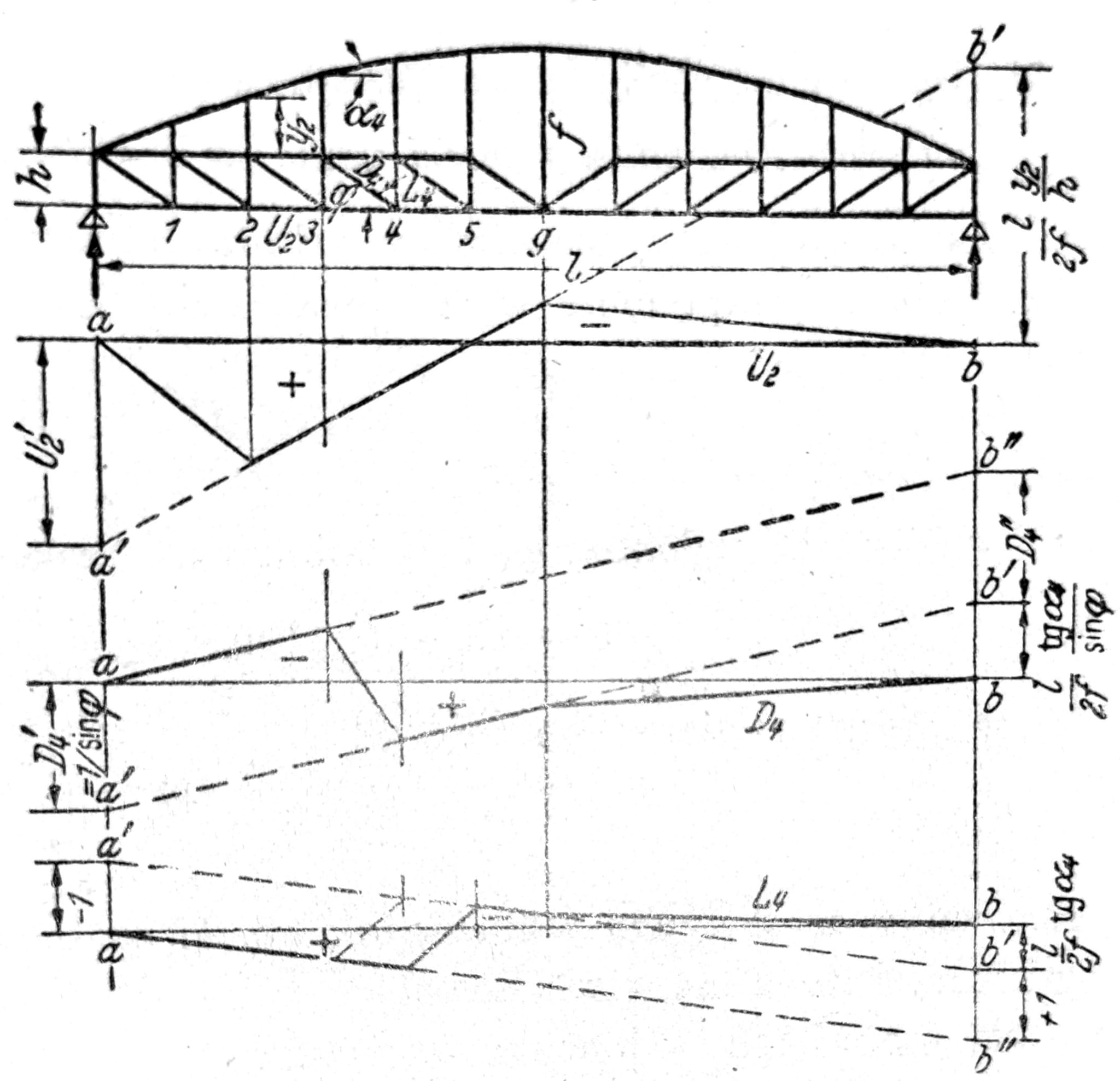
Sl. 18

Ako čvorovi trozglobnog luka sa punom gredom za ukrućenje (sl. 19) leže na kvadratnoj paraboli i ako zglob leži u osovini grede, tada su pri jednakopodeljenom opterećenju g t/m momenti savijanja M=0 na mestima vešaljki, a M=gλ²/8 u sredini polja između vešaljki.

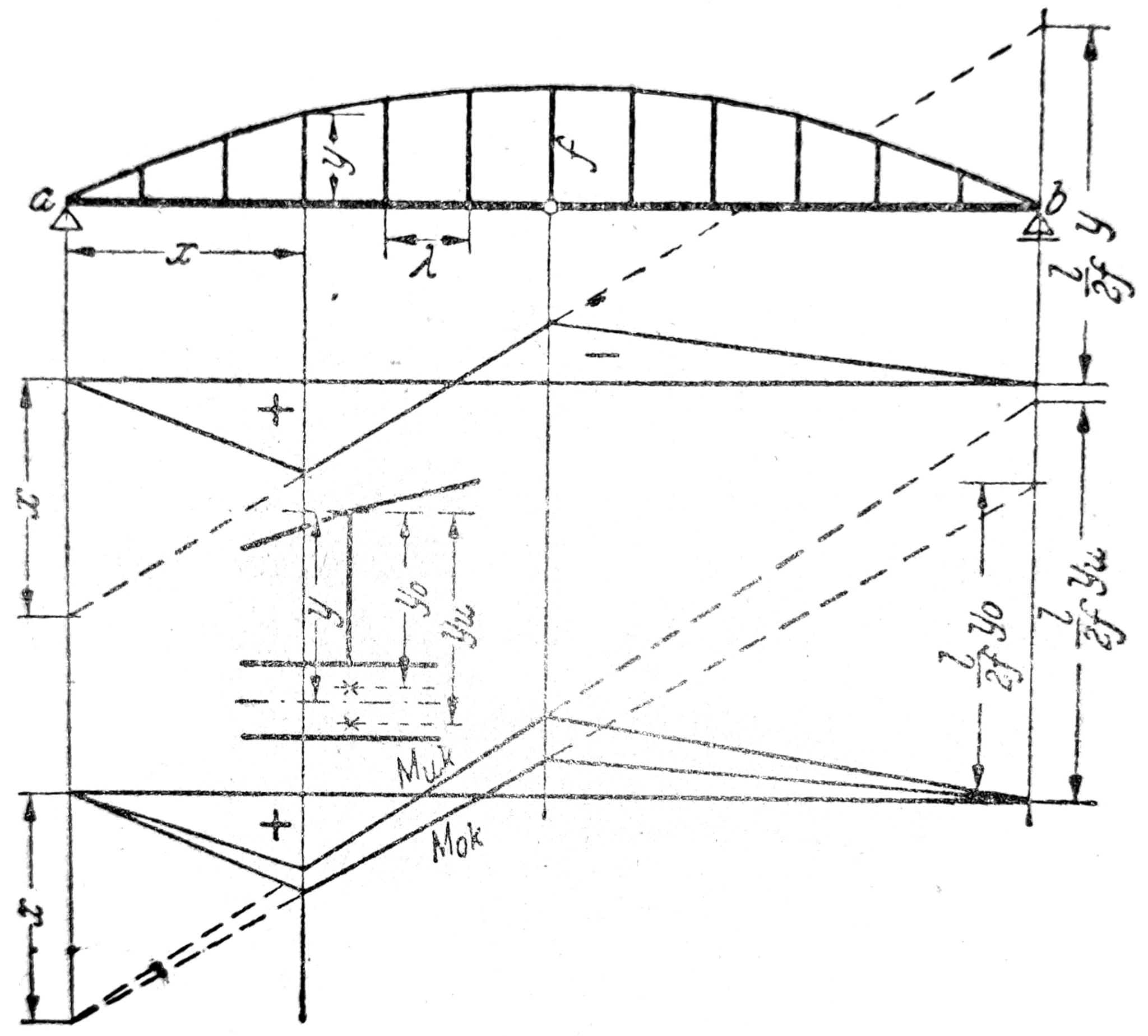
Sl. 19

 

Okvirni nosači

Sl. 20

Sl. 20 prikazuje momentni dijagram trozglobnog okvira sa prepustima i obešenim nosačima usled jednakopodeljenog punog opterećenja. Uticajna linija za moment M_e dobija se na osnovu izraza M_e=-Hh + M_k, superpozicijom uticajne linije za horizontalni potisak H (sa multiplikatorom -h) i za moment savijanja M_k na prepustu.

Pri nesimetričnom opterećenju simetričnih nosača račun se često može uprostiti rastavljanjem opterećenja na simetrično i antimetrično opterećenje, sl. 21. Specijalno to važi za okvirne nosače na sl. 22 i 23, na kojima su prikazani momentni dijagrami usled koncentrisane sile na proizvoljnom mestu gornje podvlake. Horizontalno opterećenje u visini podvlake može se shvatiti kao antimetrično. Kako se horizontalno opterećenje podvlake može smatrati i za virtualno opterećenje za proračun horizontalnih pomeranja podvlake, iz momentnih površina se može odmah zaključiti na koju se stranu pri vertikalnom opterećenju podvlaka pomera. Ova pomeranja se dobijaju kombinacijom antimetričnih ravnotežnih stanja. Prema tome, za slučajeve na sl. 22 i 23 podvlaka se pomera nadesno.

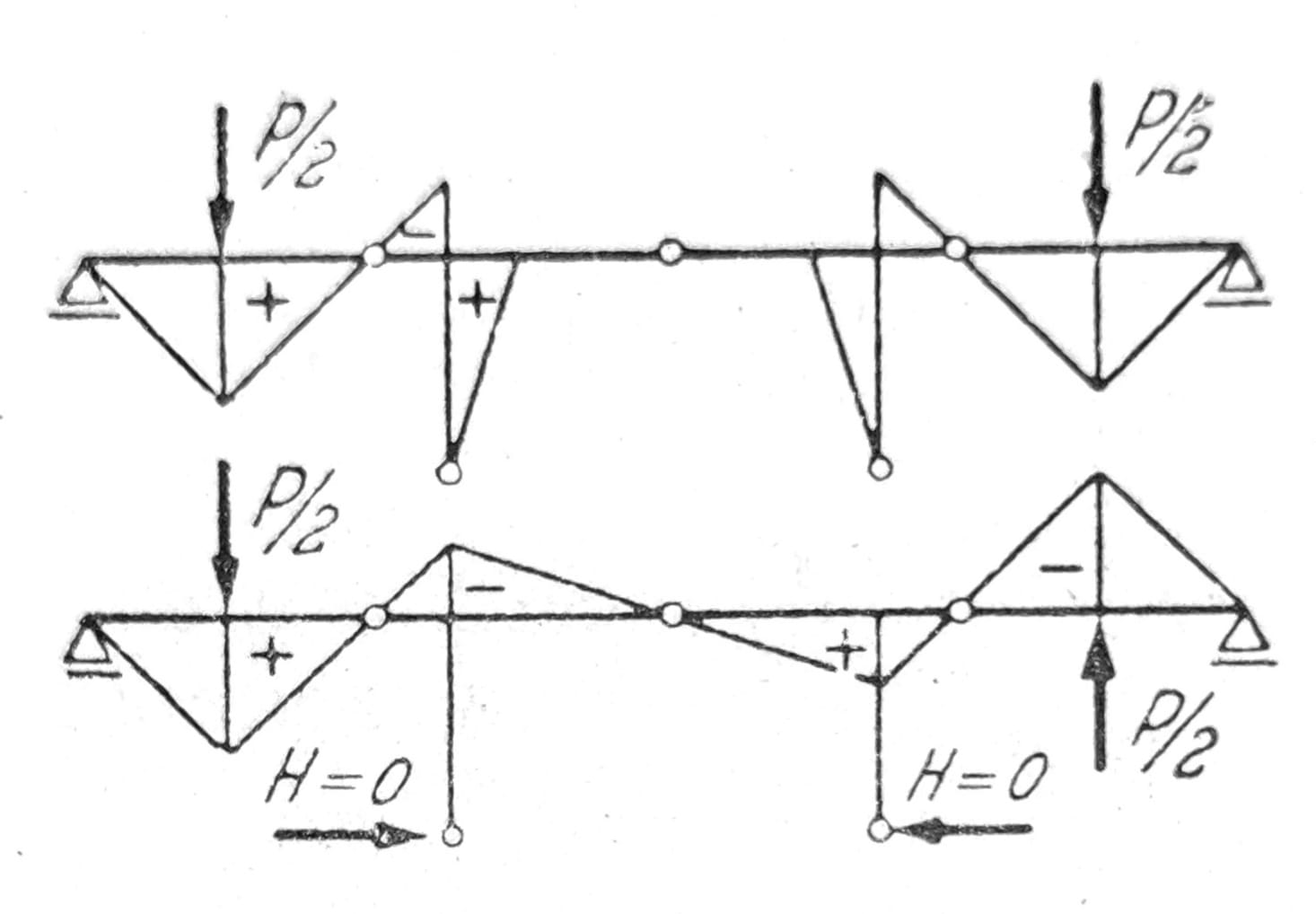
Sl. 21

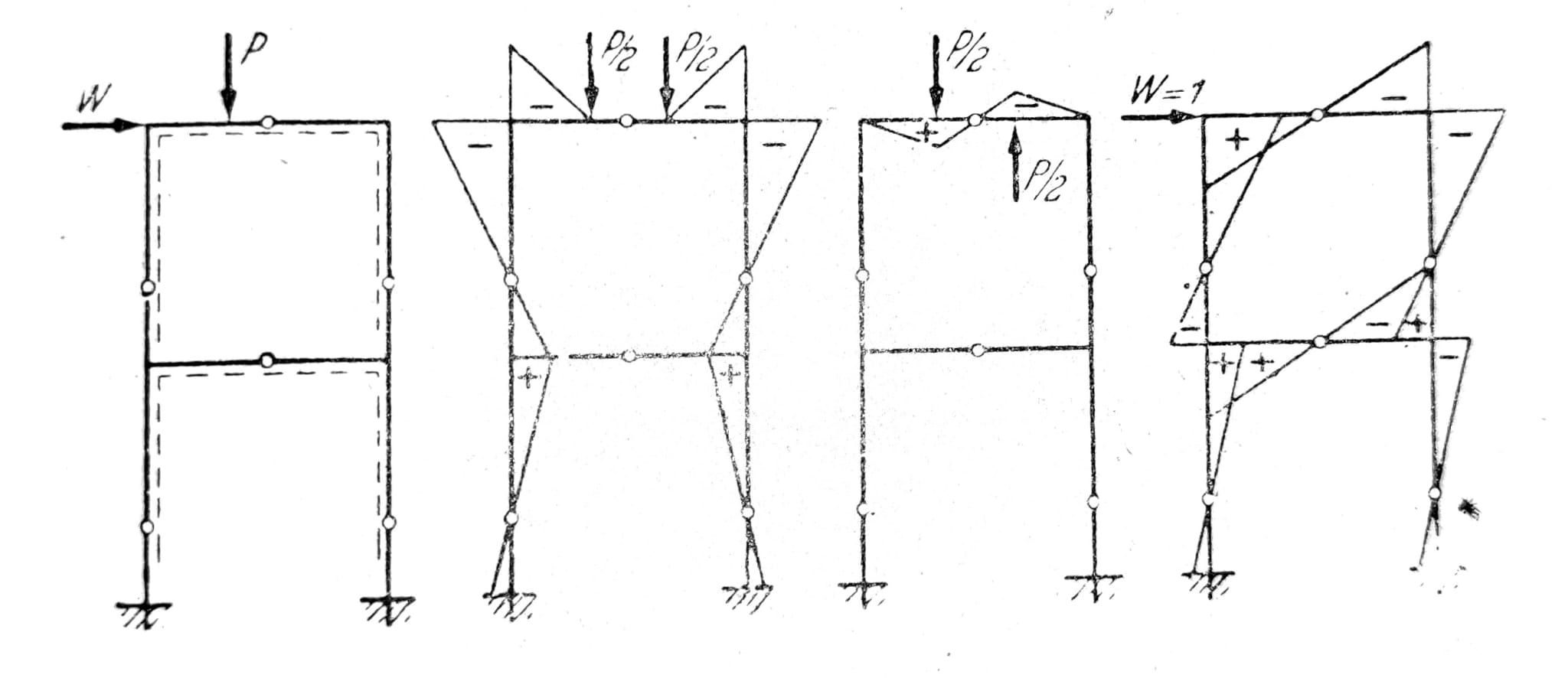
Sl. 22

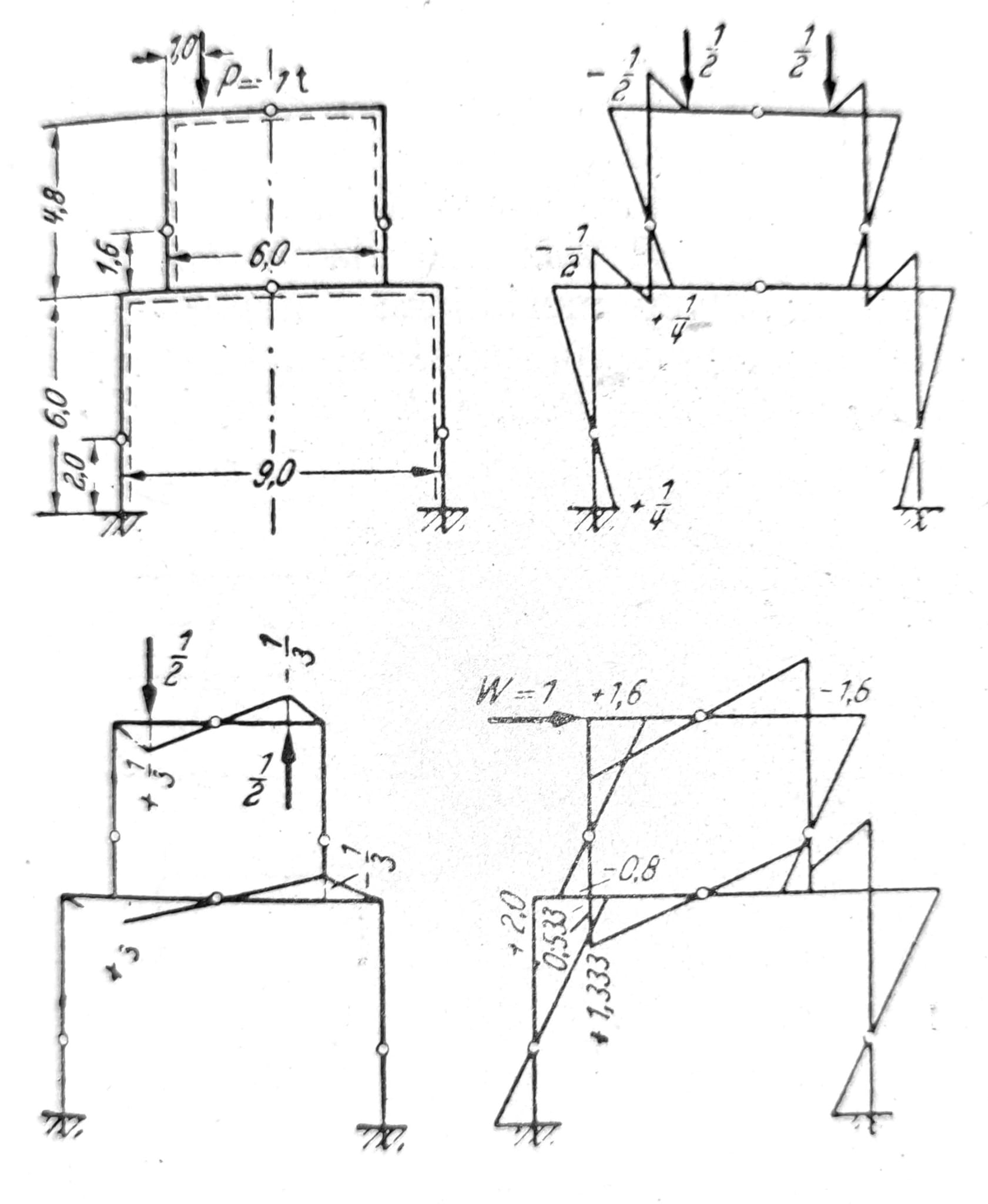
Sl. 23

 

Prostorne rešetke

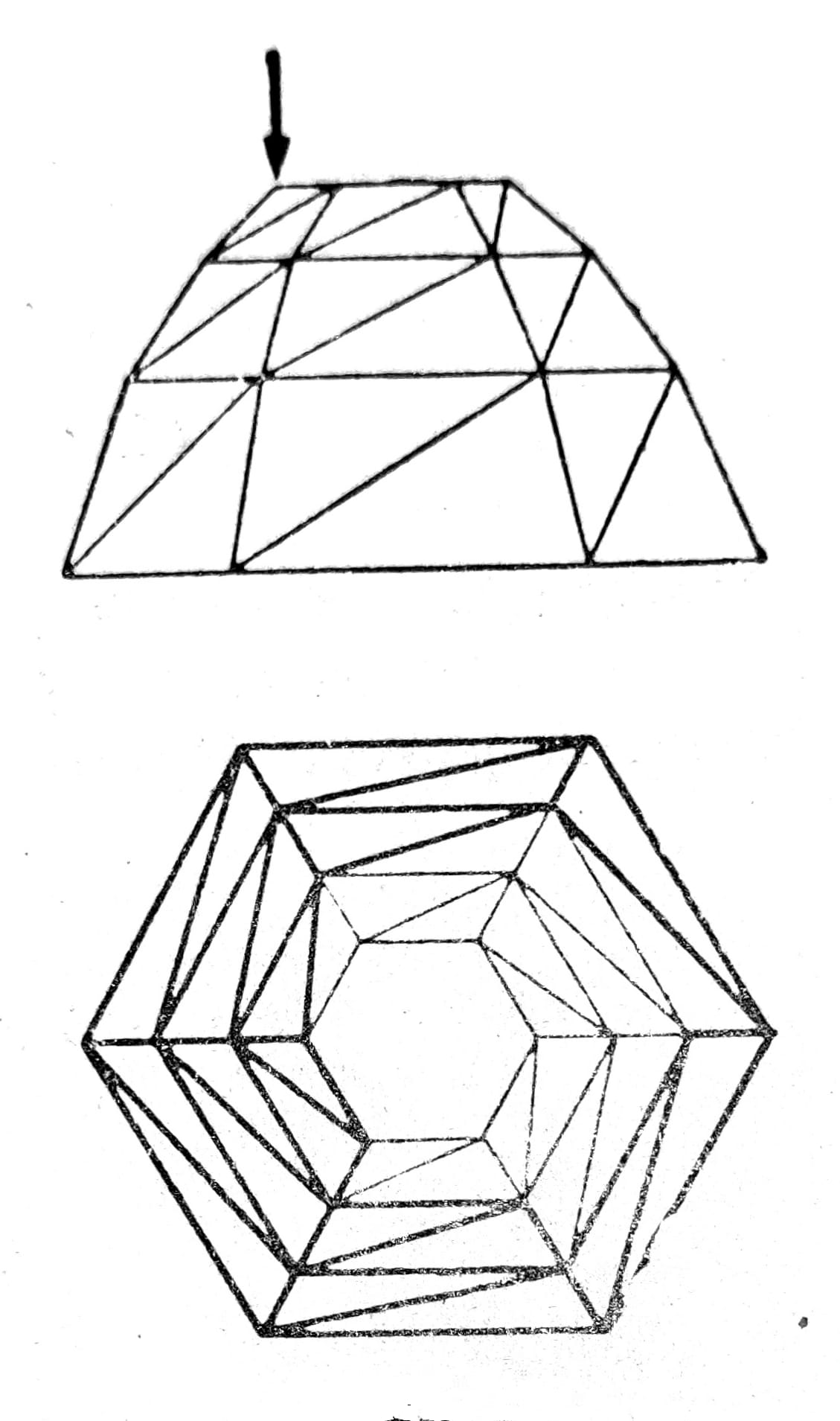
Sl. 24

Schwedler-ova kupola (sl. 24) i zarubljena rešetkasta piramida (sl. 25), kao poseban slučaj Schwedler-ove kupile kod koje meridijani nemaju preloma, sa m spratova i n strana, sastoje se od m*n meridijalnih štapova S, (m+1)n štapova prstenova R i m*n dijagonalnih štapova D. Kako je broj čvorova k=(m+1)n nosač je statički određen kada je broj oslonaca a = 3k-s = 2n, tj. kada je svako podnožno teme oslonjeno na linijsko težište sa vertikalnim i horizontalnim osloncem. Ako štapovi donjeg prstena otpadnu, u svakom temenu potrebno je nepokretno ležište sa tri oslonca. Upotrebljivost rasporeda horizontalnih oslonaca treba ispitati. Pravci oslanjanja na sl. 26 nepravilno su izabrani jer je moguće nacrtati neprotivrečan plan polova.

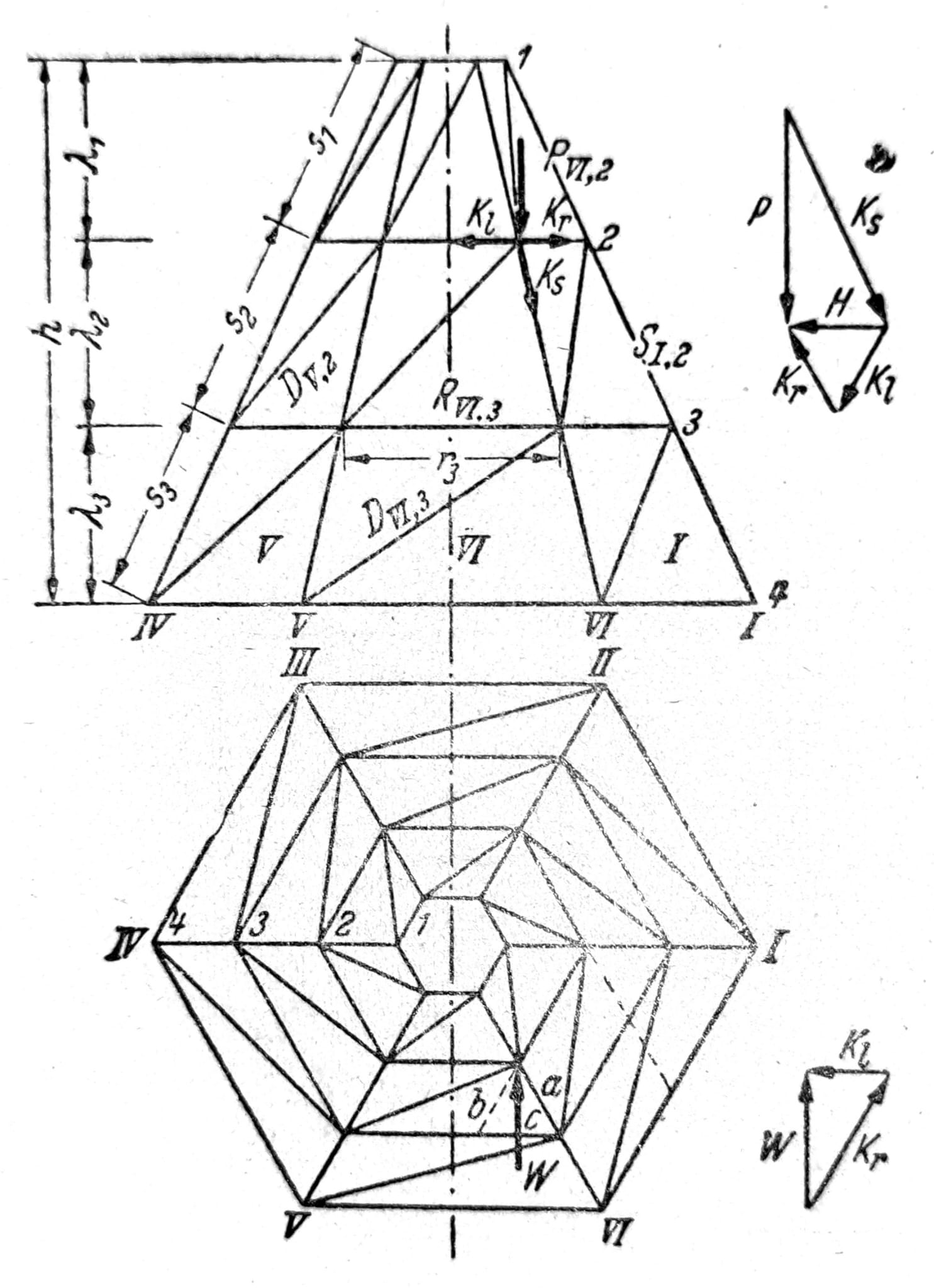
Sl. 25

Trapezi koje formiraju meridijalni štapovi i štapovi prstenova mogu se ukrutiti K-ispunom. Čvorove koje time pridolaze treba smatrati za čvorove ravne rešetke. Tereti se smeju preneti samo preko glavnih čvorova. Vertikalan teret P koji napada u čvoru biće razložen u komponentu K_s=Ps/λ u pravcu meridijana i u horizontalnu komponentu H=Pa/λ. Horizontalna komponenta razlaže se dalje na komponente u pravcu štapova prstena K_l=Hc/a=Pc/λ i K_r=Hb/a=Pb/λ.

Na isti način određuju se komponente K_l i K_r proizvoljne horizontalne sile W, tako da se za ravne ploče rešetkaste piramide dobija shema opterećenja prikazana na sl. 27. Komponente K_s u pravcu štapova meridijana nisu na slici prikazane.

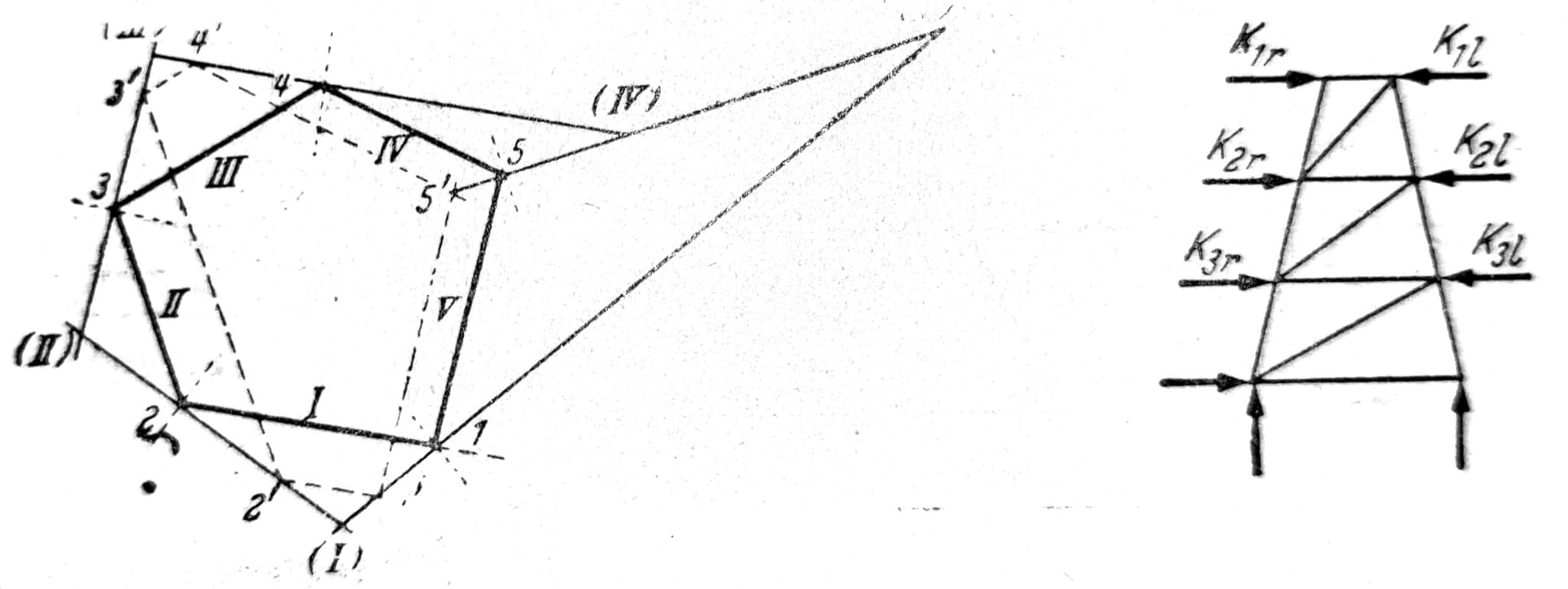
Sl. 26 i 27, respektivno

Kada su nosač i opterećenje P ciklički simetrični, tada su sile K_l jednake silama K_r, pa su dijagonale nenapregnute dok su sile u štapovima meridijana:

S₁ = -P₁s/λ;   S₂ = -(P₁+P₂)s/λ;   S₃ = -(P₁+P₂+P₃)s/λ

a u štapovima prstena:

R_i = P_ib/λ

Proračun Schwedler-ove kupole može se sprovesti na isti način kada se svaki sprat shvati kao rešetkasta piramida. Osim aktivnih sila P i W, treba tada uvesti kao spoljašnje sile i sile u štapovima S i D gornjeg sprata, odn. njihove komponente u pravcu štapa meridijana i štapova prstena. Dok se kod rešetkaste piramide uticaj jedne koncentrisane sile oseća samo u štapovima dveju susednih ploča, dotle se kod Schwedler-ove kupole njen uticaj proteže na znatno veći broj štapova. Na sl. 24 označeni su štapovi koji su napregnuti usled sile P u temenom prstenu.