Torzija

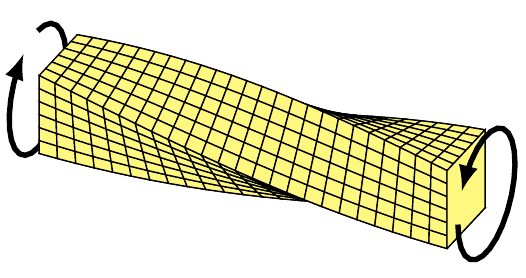
Saint-Venant-ova teorija torzije (slobodna torzija)

Diferencijalna jednačina

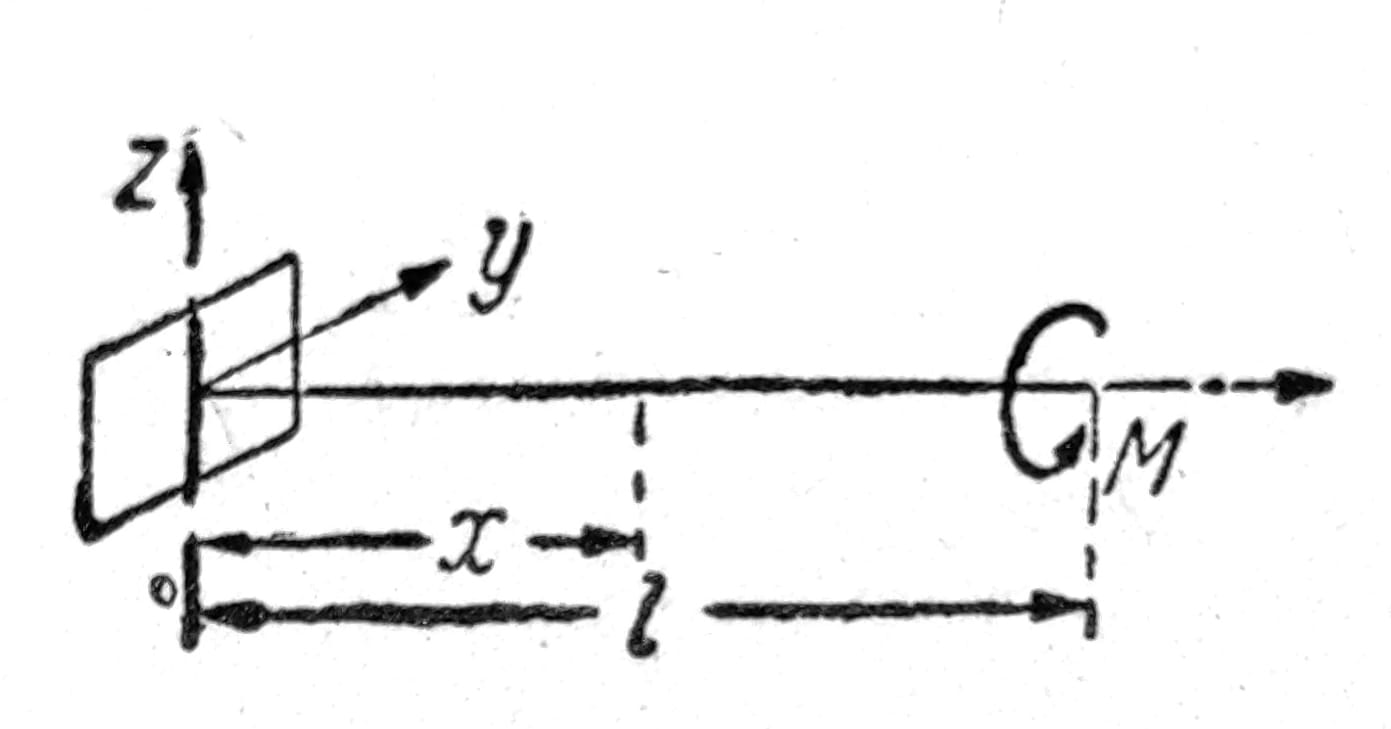
Sl. 1

Neka je prav štap učvršćen na jednom od njegovih krajeva x=0 i neka je na drugom kraju opterećen momentom torzije M (sl. 1). Tada se svaki njegov presek obrće za izvestan ugao α(x) oko određene prave paralelne sa osovinom štapa koju ćemo usvojiti za x-osovinu. Ako su svi preseci međusobno jednaki, svaka prava paralelna sa x-osovinom preći će u zavojnicu, a ugao α će biti proporcionalan odstojanju od učvršćenog kraja: α=ϑx, odakle proizilaze komponentalna pomeranja u ravni preseka (sl. 2):

v = - r a sinψ = - ϑ x z,

w = r a cosψ = ϑ x y.   (1a)

Veličina ϑ se naziva ugao torzije (dimenzija: dužina^-1, obrtanje na jedinicu dužine). Ugao torzije je proporcionalan momentu torzije M:

ϑ = M/GJ_T.   (2)

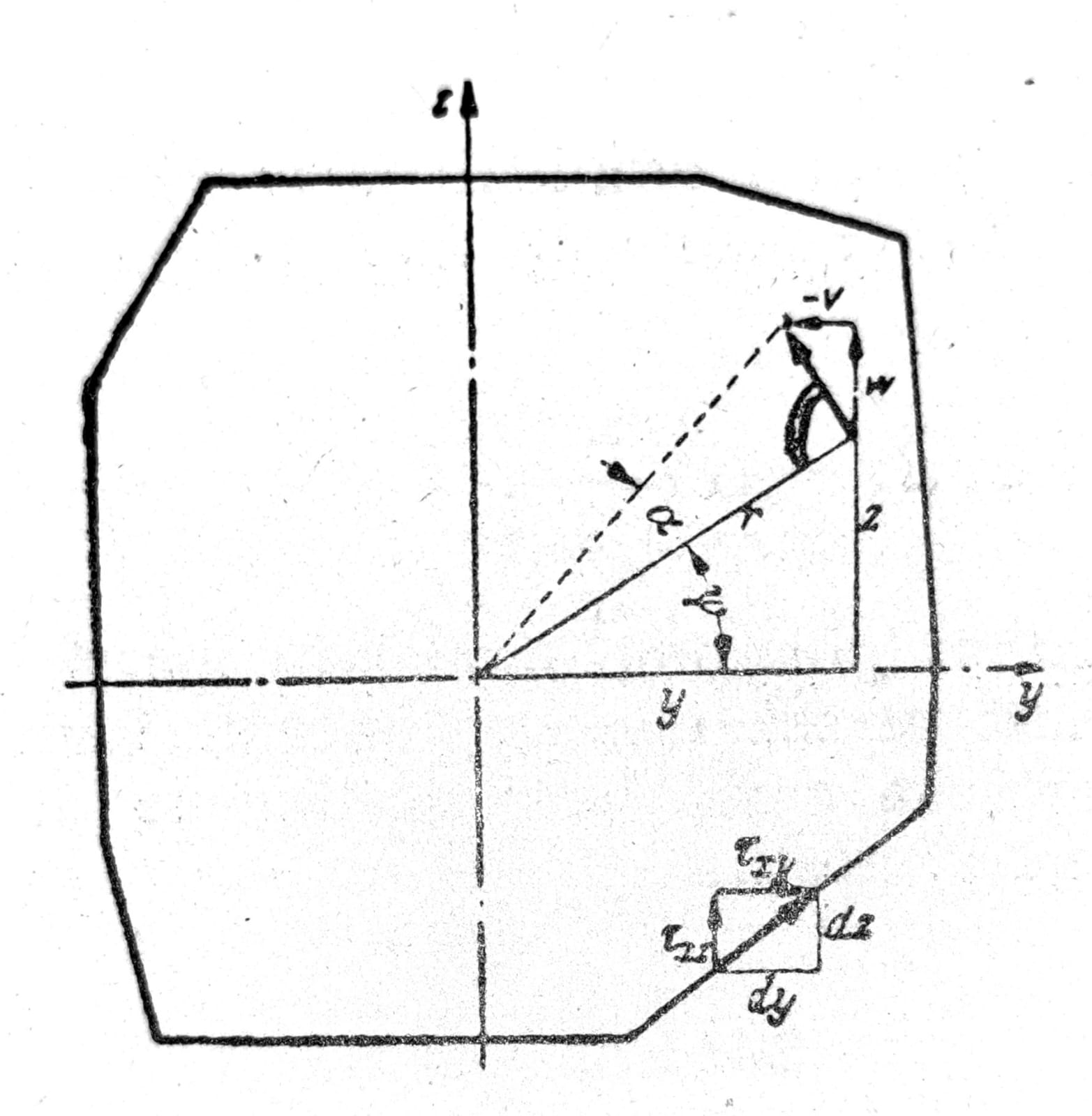
Sl. 2

Faktor proporcionalnosti GJ_T, krutost pri torziji, jednak je proizvodu modula smicanja G i faktora J_T, koji predstavlja uticaj oblika i veličine preseka.

Ovo obrtanje preseka ne predstavlja jedinu deformaciju štapa. Pored toga dolazi još i do krivljenja preseka, tj. do pomeranja u u pravcu x-osovine, koja ima istu veličinu za odgovarajuće tačke svih poprečnih preseka i prema tome je samo funkcija koordinata u ravni preseka, a inače je proporcionalno opterećenju M ili uglu torzije ϑ:

u = u(y,z) = ϑ ∙ φ(y,z),   dφ/dx=0.   (1b)

Ako se u odgovarajuće jednačine pomeranja uvedu izrazi iznad, dobija se da su glavni normalni naponi jednaki nuli, pa ostaju samo dva komponentalna napona τ_xy i τ_xz:

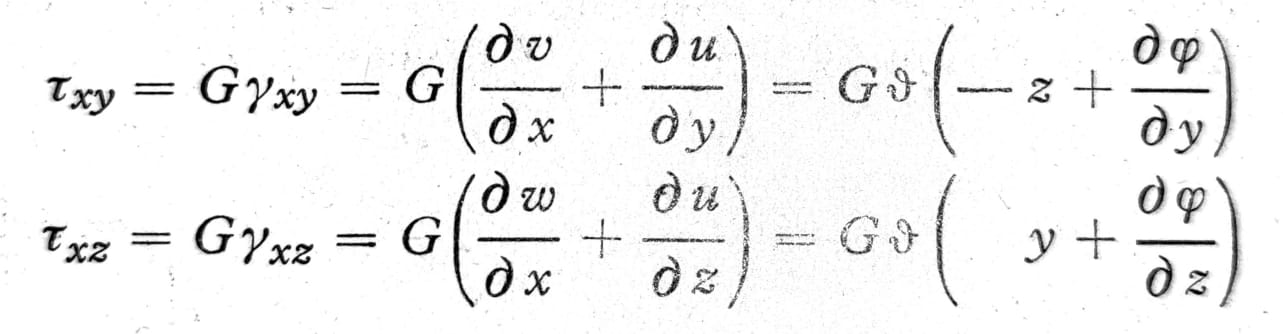
Jedn. 3

Diferencijalna jednačina problema torzije dobija se na osnovu jednačina (3) stavljajući:

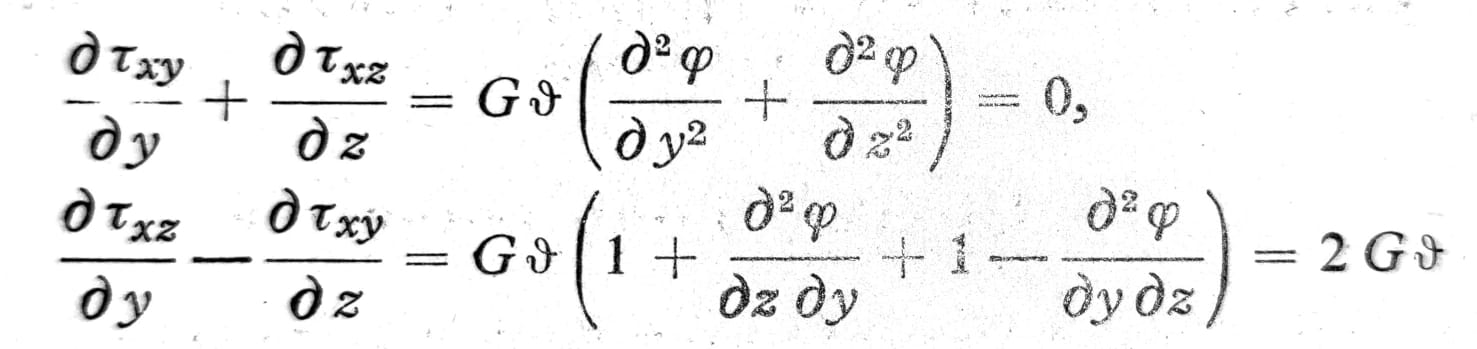
Jedn. 4a i 4b

i rešavajući ove diferencijalne jednačine po nepoznatim τ_xy i τ_xz uvođenjem funkcije napona F(y,z) da je:

τ_xy = - dF/dz,   τ_xz = + dF/dy.   (5)

Ovim je jednačina (4a) identički zadovoljena, a iz jednačine (4b) dobija se tražena diferencijalna jednačina

d²F/dy² + d²F/dz² = 2Gϑ  (6)

Granični uslov potreban za jednoznačno rešenje ove jednačine dobija se iz zahteva da na omotaču štapa nema smičućih napona, odakle zbog konjugovanosti smičućih napona proizilazi da napon u ravni preseka ne sme duž konture da ima komponentu upravnu na nju. Odavde je, sl. 2:

dy/dz = τ_xy/τ_xz = - (dF/dz) / (dF/dy)

dakle

dF/dy dy + dF/dz dz = 0,

tj. totalni diferencijal funkcije F mora da bude nula, odnosno potrebno je da bude F=const. duž konture.

Ako presek ima samo jednu konturu, može se na ovoj staviti prosto F=0, jer kod funkcije napona, od koje nas ustvari interesuju samo izvodi, ne igra ulogu proizvoljna aditivna konstanta. Kod preseka koji imaju više od jedne konture ovo pitanje je složenije.

Kao što se vidi iz jednačine (5) rezultanta smičućih napona τ_xy i τ_xz u proizvoljnoj tački preseka jednaka je po veličini gradijentu funkcije napona F, ali je na njega upravna, tj. ima pravac tangente na liniju F=const.

Rešenjem diferencijalne jednačine (6) dobijaju se naponi τ kao funkcije od y, z i ϑ. Zadatak proračuna je, razume se, određivanje ugla torzije ϑ i napona, posebno maksimalnog napona kao funkcije momenta torzije, dakle, određivanje krutosti preseka J_T iz jednačine (2) i otpornog momenta torzije W_T = M_maxτ. Da bi se ovi dobili potrebno je samo da se M izrazi u funkciji od F:

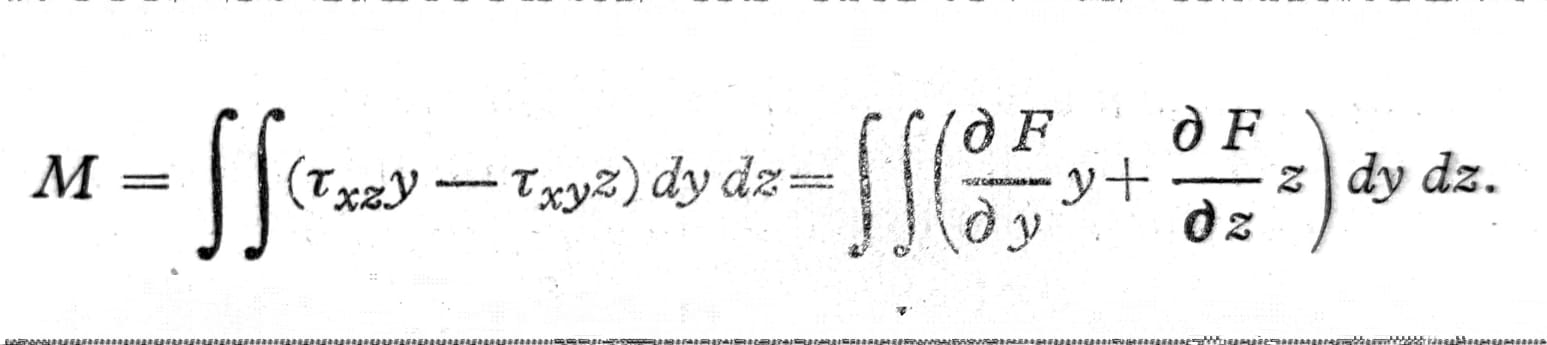
Oba sabirka ovog integrala, koga treba uzeti po celom preseku, mogu se transformisati parcijalnim integriranjem. Ako se, npr. prvi od njih integrira najpre duž linije z=const. od tačke na konturi y=y₁ do tačke y=y₂ (sl. 3) i pri tome uzme u obzir da je u obe ove tačke F=0, dobija se

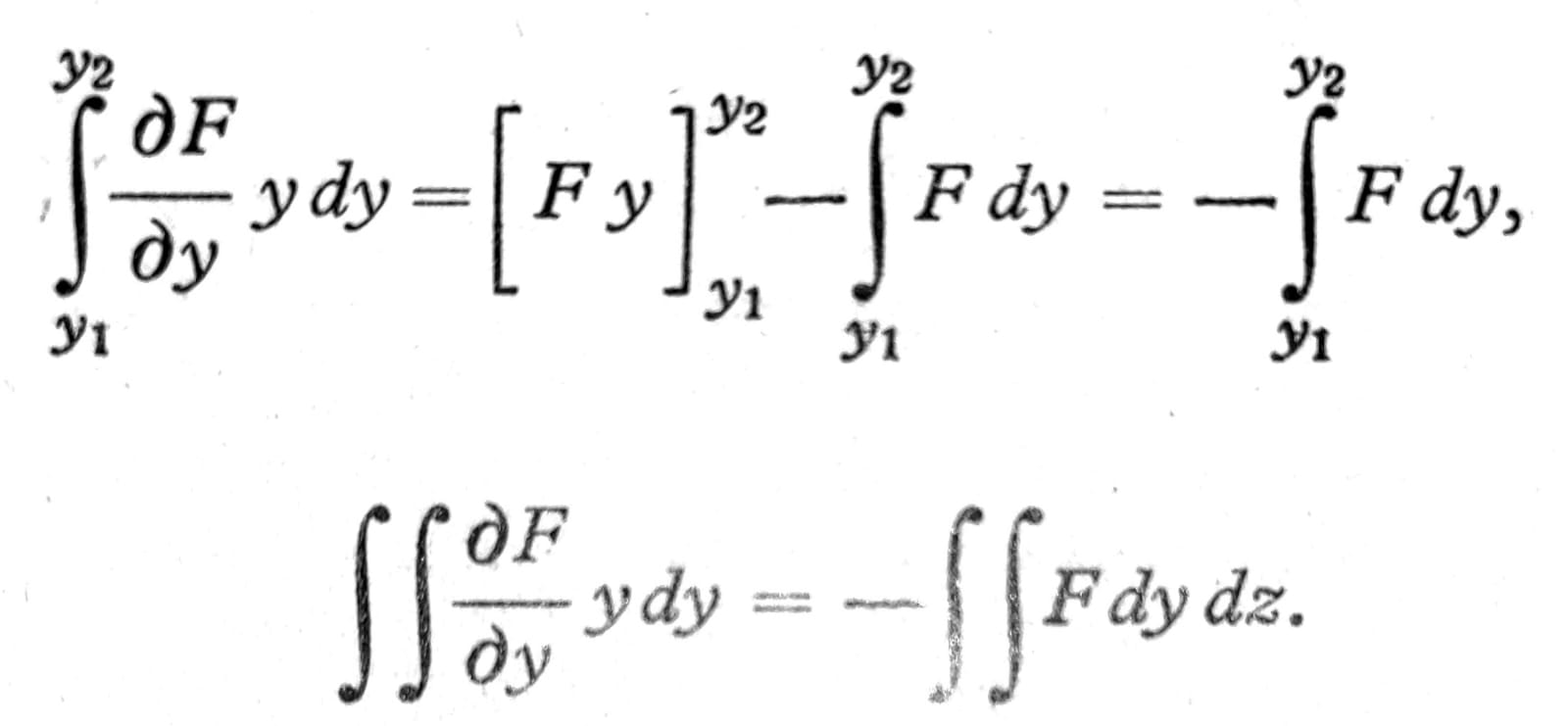
Iz drugog integrala dobija se ista vrednost, tako da je

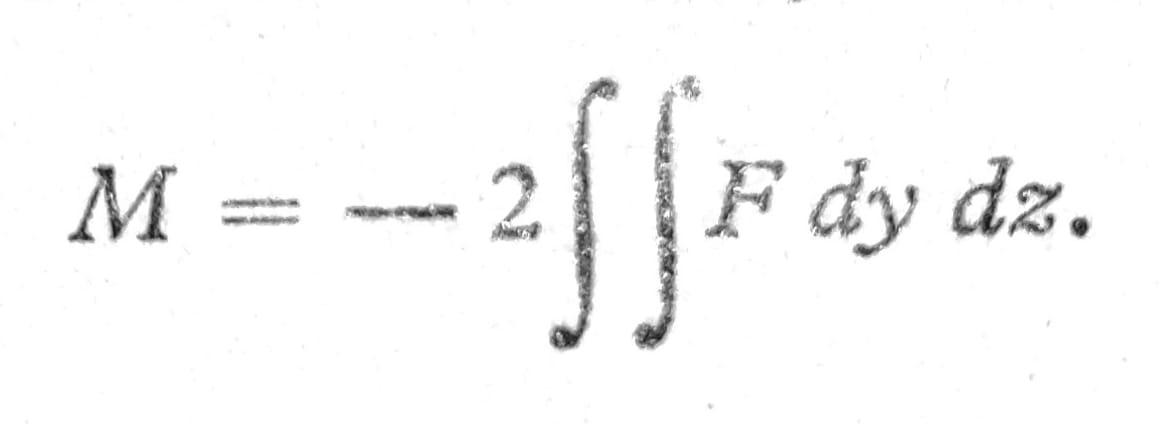
Jedn. 7

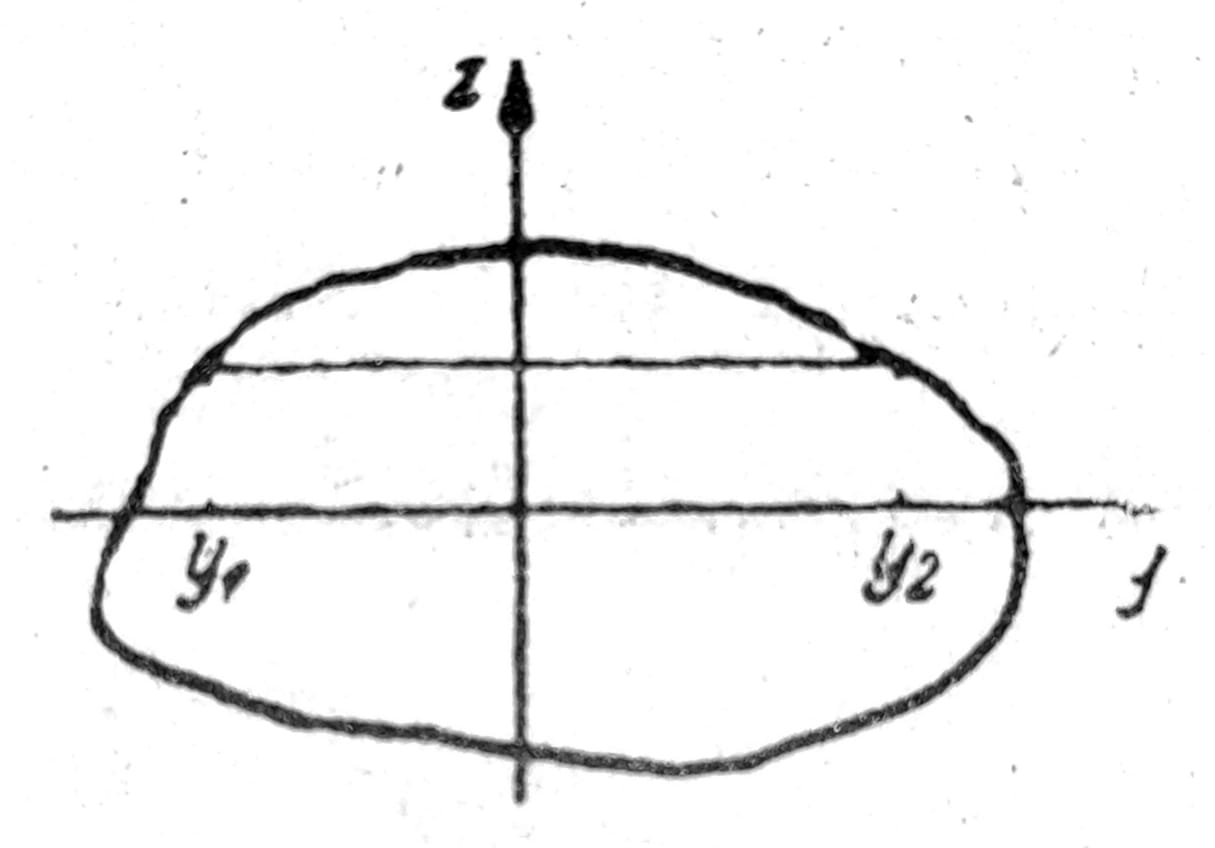
Sl. 3

Drugi slučajevi punih preseka

Diferencijalna jednačina (6) je nehomogena jednačina teorije potencijala. Prema tome za rešenje problema torzije u slučaju proizvoljnog poprečnog preseka stoje na raspolaganju metode teorije potencijala, koje omogućuju da se ono uvek nađe. Ove metode su, međutim, uopšte uzev, isuviše složene da bi se mogle primeniti na pojedine slučajeve koji se javljaju u praksi. Zato su u sledećoj tablici dati rezultati ovakvih proračuna za nekoliko preseka.

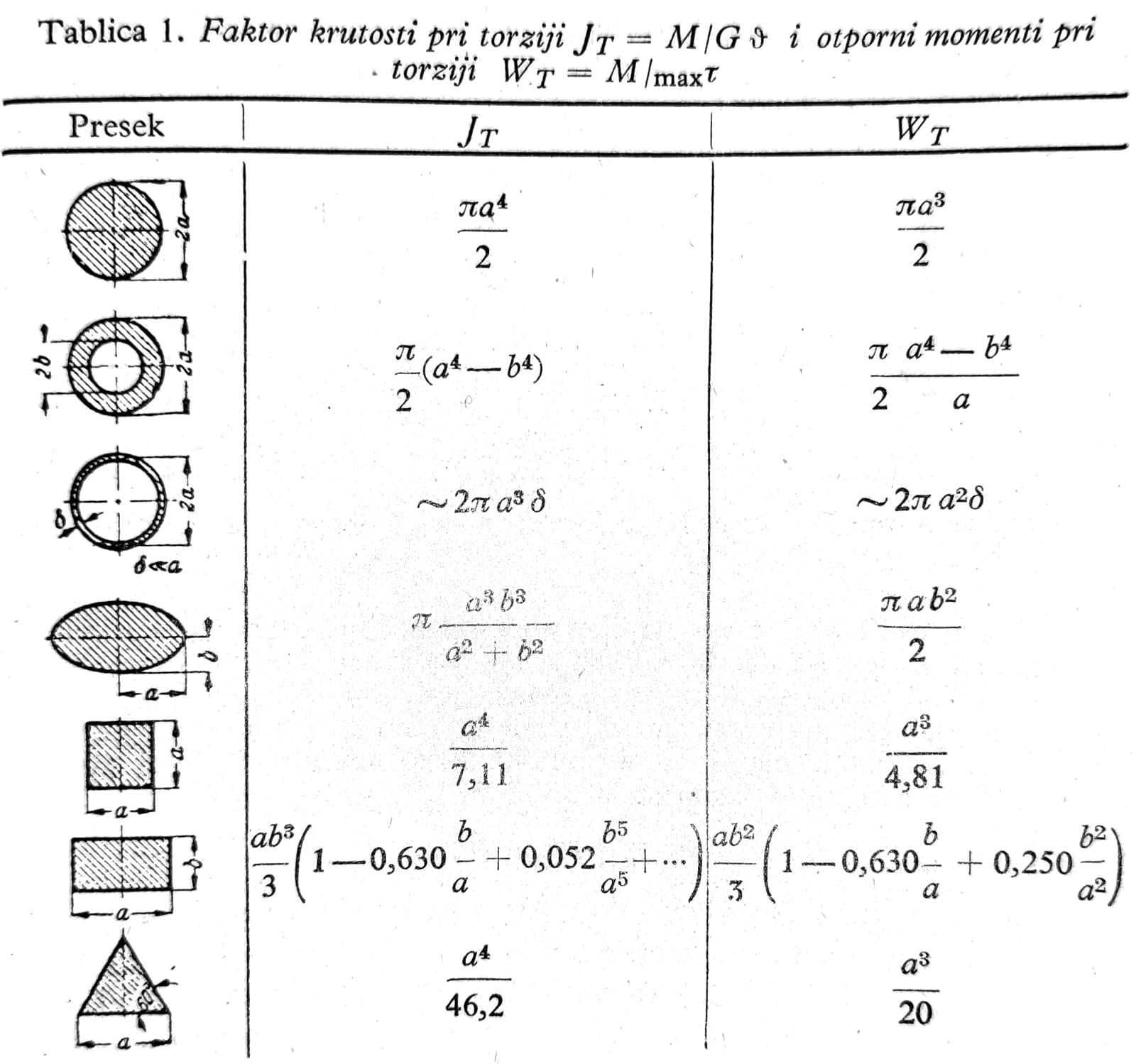
Za preseke bliske kružnom može se staviti J_T=F⁴/40I_p, pri čemu je F površina, a I_p polarni moment inercije preseka.

Analogija sa membranom

Dobru pomoć za procenjivanje torzionih napona, a istovremeno i jedan postupak za njihovo tačno određivanje pruža analogija između funkcije napona F problema torzije i ugiba transverzalno opterećenje membrane. Neka je na ravnom zidu nekog suda prosečan otvor koji je podudaran sa poprečnim presekom štapa opterećenog na torziju. Kada se preko ovog otvora zategne membrana i u sudu izazove mali višak pritiska p, membrana se ispupči upolje, tako da njeni ugibi ξ(y,z) zadovoljavaju diferencijalnu jednačinu

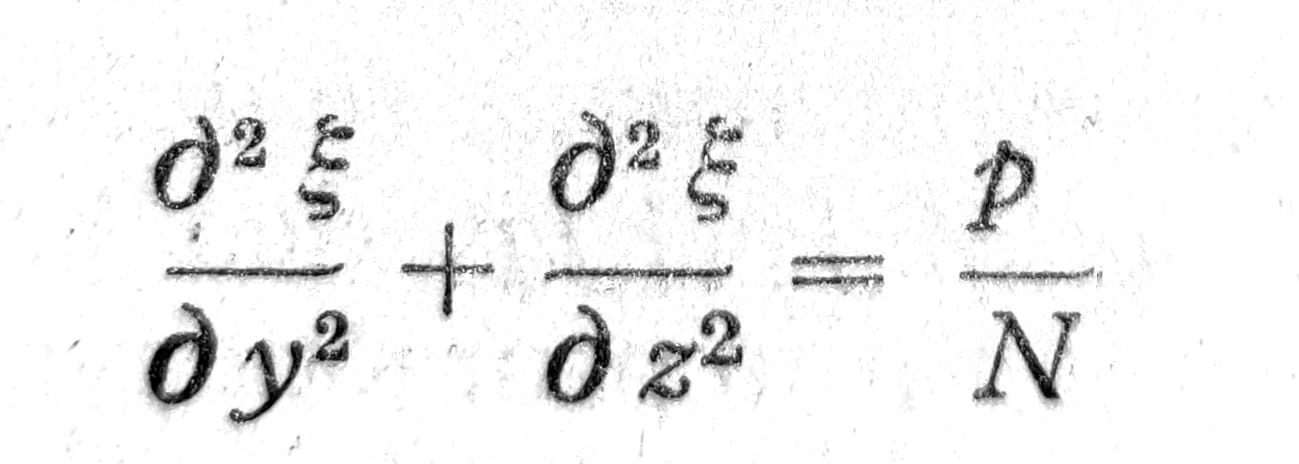
gde je N površinski napon u membrani izazvan kapilarnim silama (dimenzije: sila po jedinici dužine). Ova jednačina se podudara sa jednačinom (6), a i granični uslov ξ=0 je isti kao i kod funkcije napona. Na taj način može se pomoću ovog ogleda sa membranom dobiti funkcija napona F(y,z) i time rešiti problem torzije. Naponu τ pri tome odgovara nagib membrane u odnosu na y-z-ravan, pa je najstrmije mesto ono na kome štap izložen torziji ima najveći smičući napon.

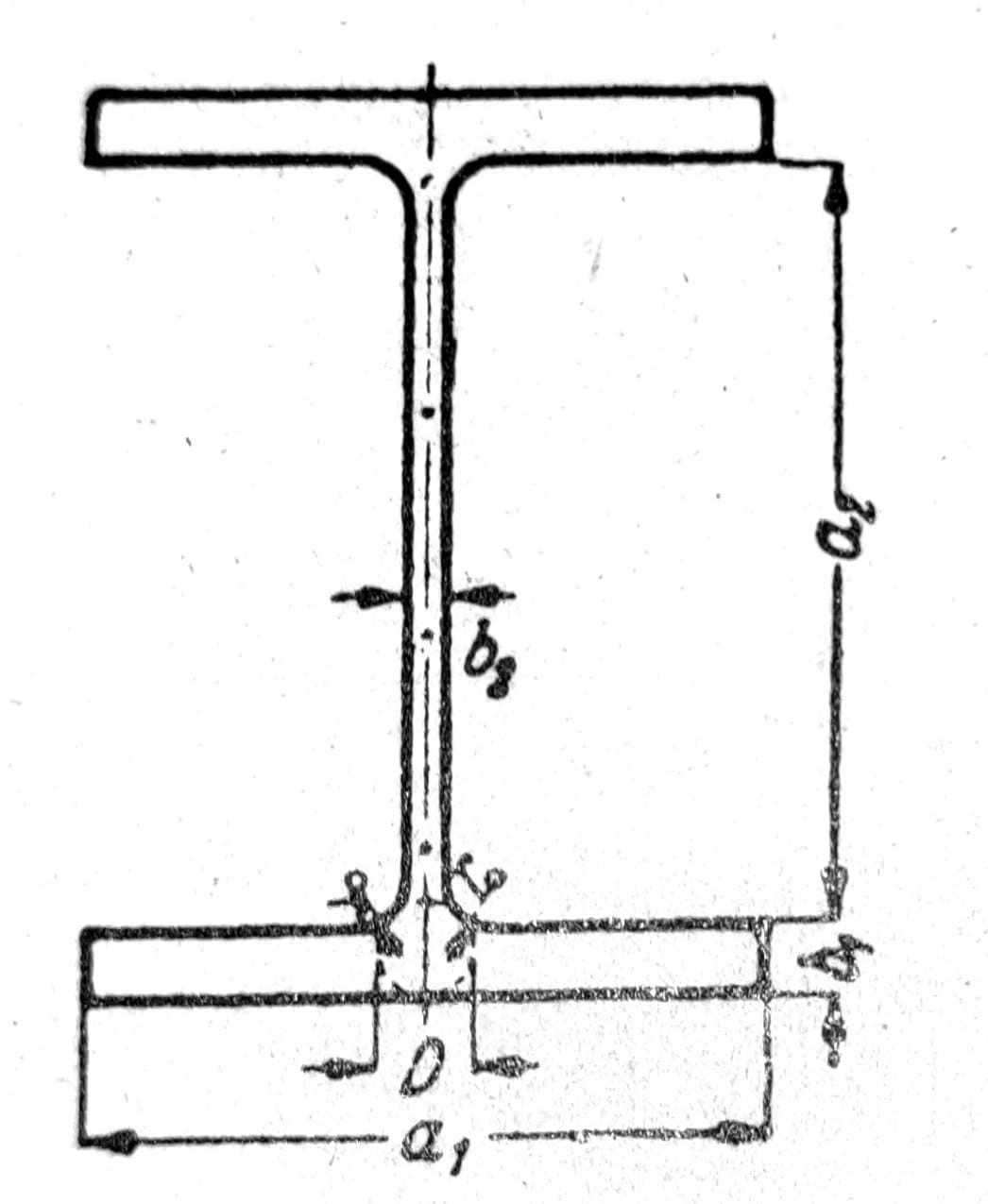
Sl. 4

Sl. 5

Ovaj postupak sa membranom je naročito pogodan za dobijanje približnih obrazaca za preseke sa tankim zidovima. Kada se, npr., I-presek izdeli prema sl. 4 na tri pravougaonika i za svaki od njih posebno sprovede analogija sa membranom, zbir zapremina dobivenih ispupčenja biće samo neznatno manji od zapremine koja stvarno odgovara funkciji napona. Prema tome je, kada su debljine b₁ i b₂ male, približno

J_T = 2J_T1 + J_T2,

pri čemu su J_T1 i J_T2 faktori krutosti pojedinih pravougaonika koji se mogu izračunati na osnovu tablice 1. Bolje približavanje se dobija kada se za rebro stavi J_T2 = a₂ b³₂/3, dakle, kada se rebro smatra za deo vrlo izduženog pravougaonika. Još tačnija vrednost dobija se prema Trayer i March-u iz

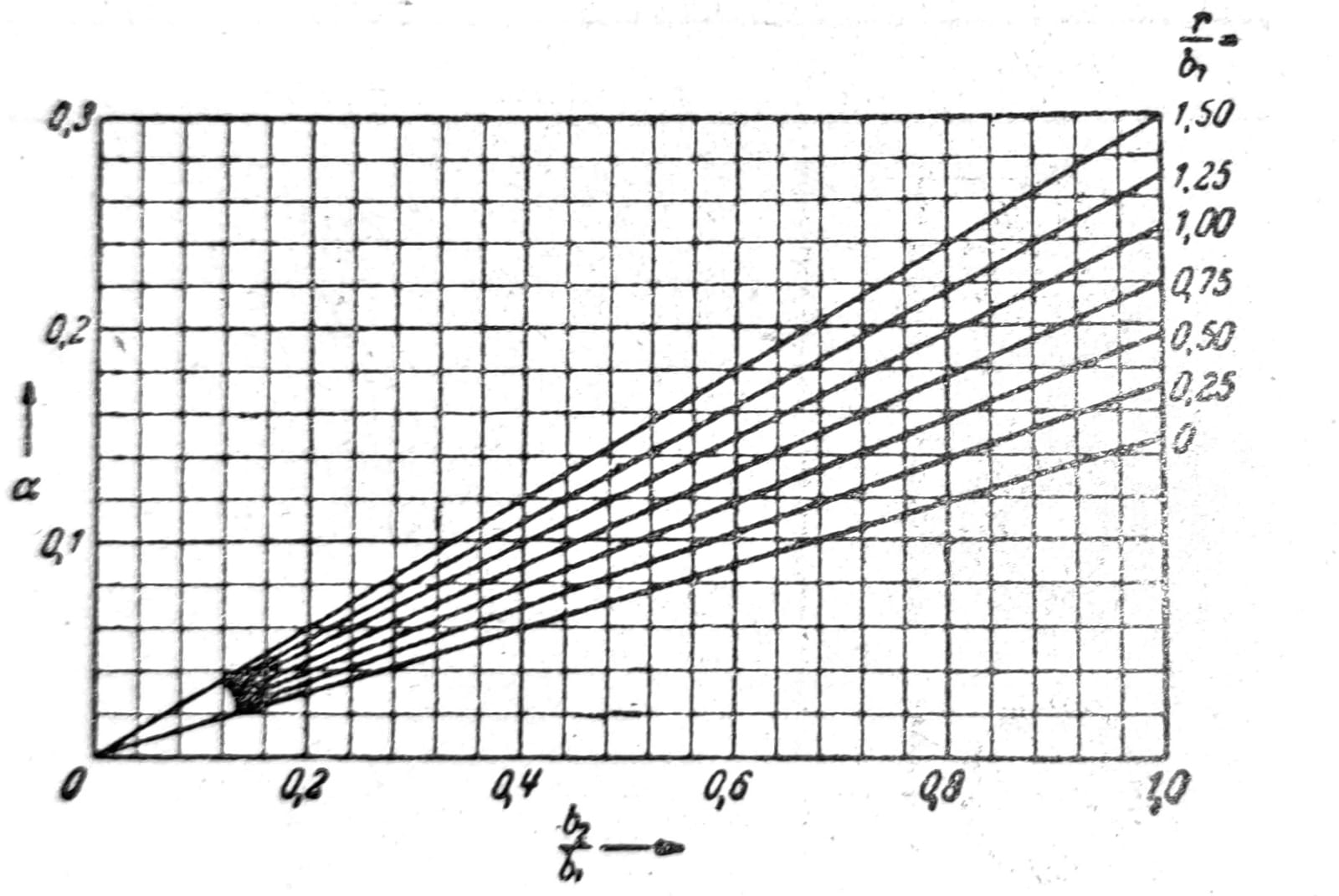
J_T = 2J_T1 + 1/3 a₂ b³₂ + 2 α D⁴,

gde je D prečnik najvećeg kruga upisanog kako je pokazano na sl. 4, a α se može uzeti iz sl. 5. Za T-presek dobija se slično tome

J_T = J_T1 +J_T2 + α D⁴,

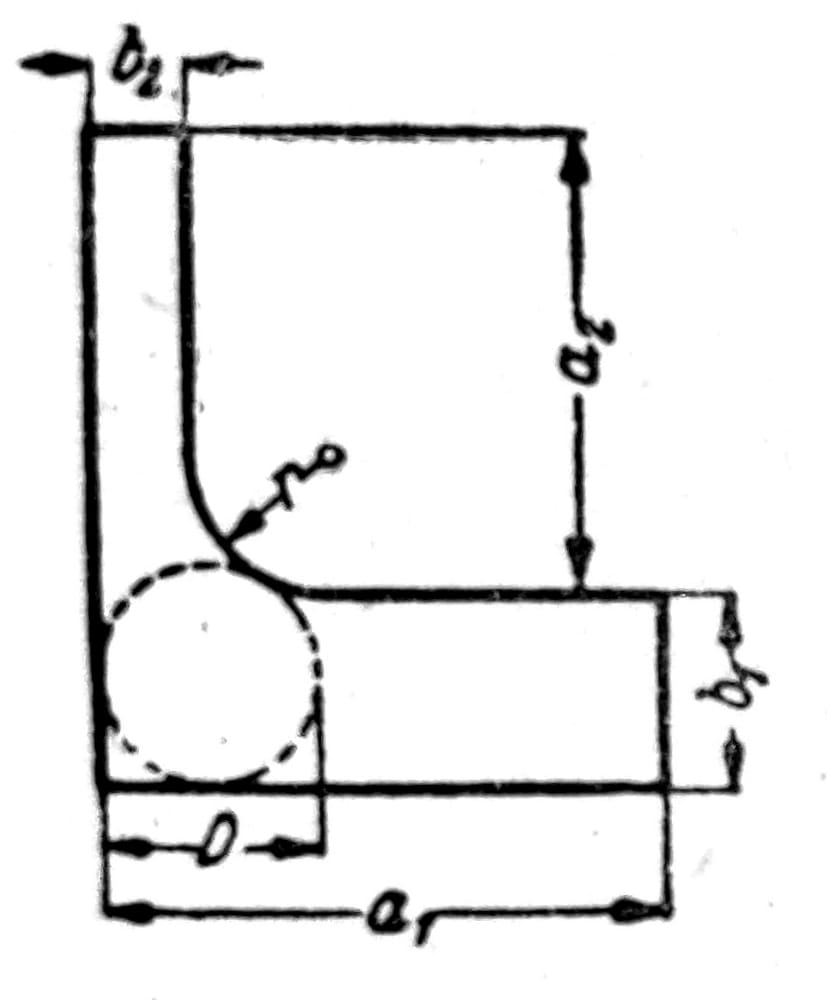
gde je J_T2 polovina vrednosti sračunate prema tablici 1 za a=2 a₂, b=b₂. Za L-preseke (sl. 6) je slično tome

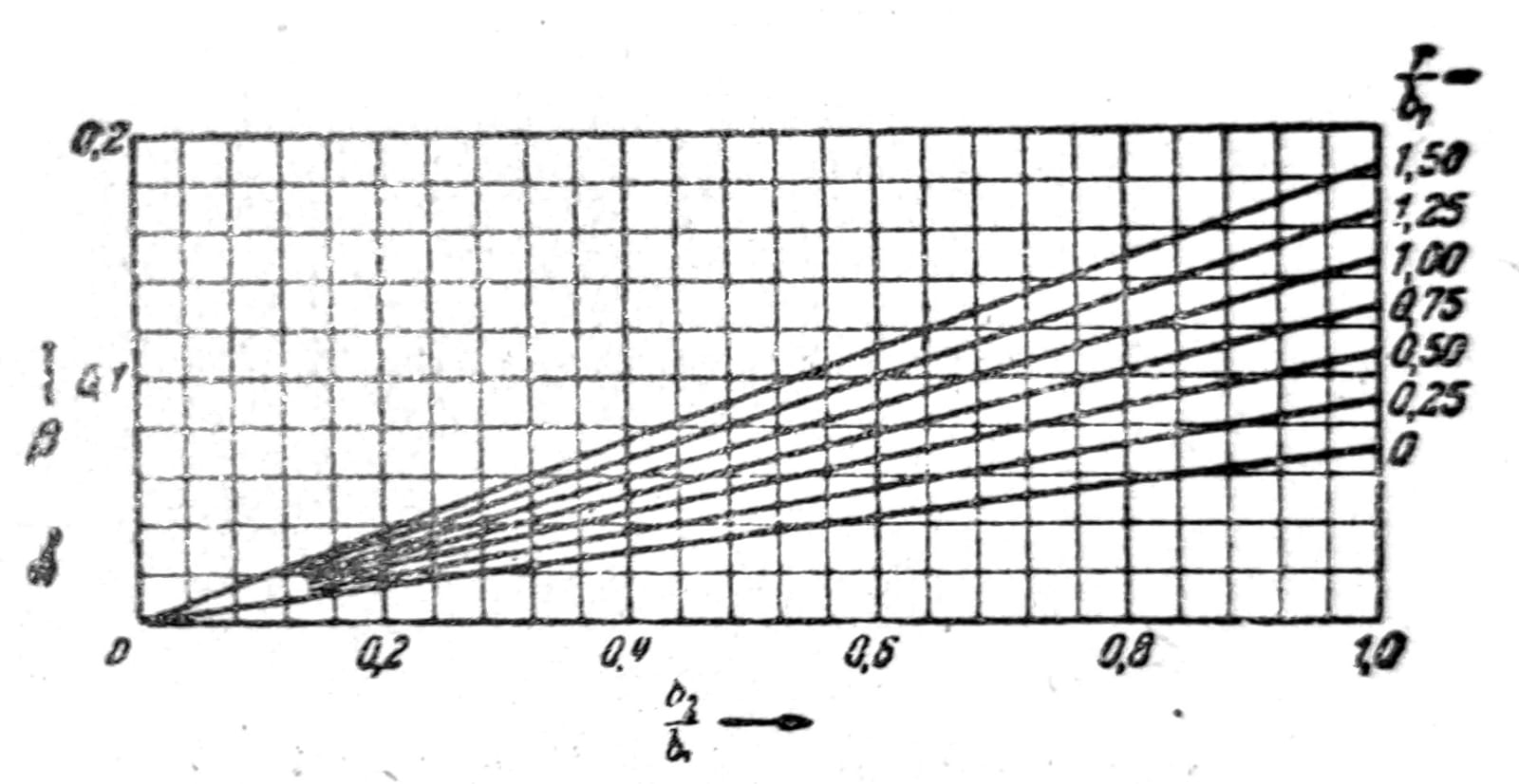
J_T = J_T1 + J_T2 + β D⁴

gde se J_T1 za deblji krak uzima neposredno iz tablice 1, dok se J_T2 za tanji krak sračunava kao i kod T-preseka, a β se uzima iz sl. 7.

Sl. 6

Sl. 7

Pri proračunu napona moment torzije se deli na sastavne pravougaonike: deo koji otpada da flanše M₁=M J_T2/J_T; smičući napon se zatim proračunava na sredini duže strane svakog pravougaonika na osnovu tablice 1. Najveći od ovih napona ne mora da bude i najveći smičući napon koji se pojavljuje u preseku. Naime, ako upadni ugao nije zaobljen, dobija se na tom mestu τ=∞, tako da se za vrlo malo poluprečnik zaobljenja ovde može očekivati najveći smičući napon.

Za jednokraki ugaonik čije je debljina krakova t prema Trefftz-u je na zaobljenju prečnika r:

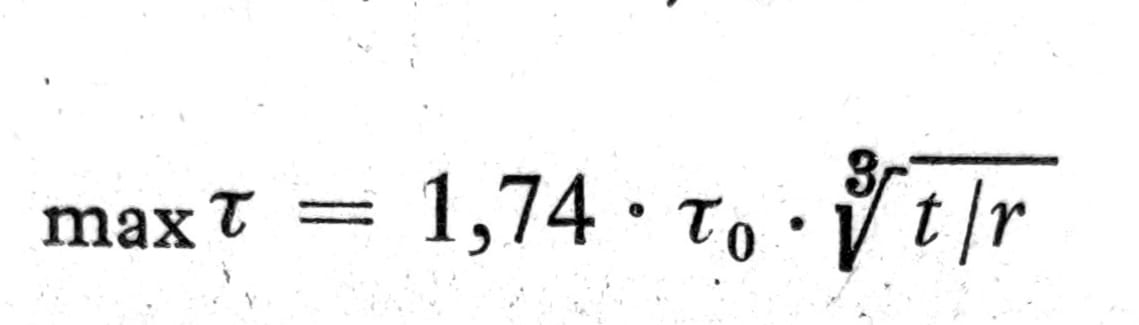
gde je sa τ₀ označen najveći napon sračunat za svaki pojedini krak na osnovu ovde opisanog postupka. Za veće poluprečnike zaobljenja može se usvojiti τ=2τ₀.

Cevi sa tankim zidovima (Bredt-ovi obrasci)

Kod cevi sa tankim zidovima ispupčena membrana ima oblik prikazan na sl. 8, koji se sastoji od zaravni iznad šupljeg prostora unutar cevi i jedne kose površine koja ovu okružuje i leži nad efektivnim presekom zida cevi; ova kosa površina mora utoliko da bude strmija ukoliko su na odgovarajućem mestu zidovi cevi tanji. U ovom slučaju smičući naponi su po debljini zidova raspoređeni prilično ravnomerno i obrnuto su proporcionalni debljini zidova tj. sila smicanja T = τt se ne menja duž obima preseka.

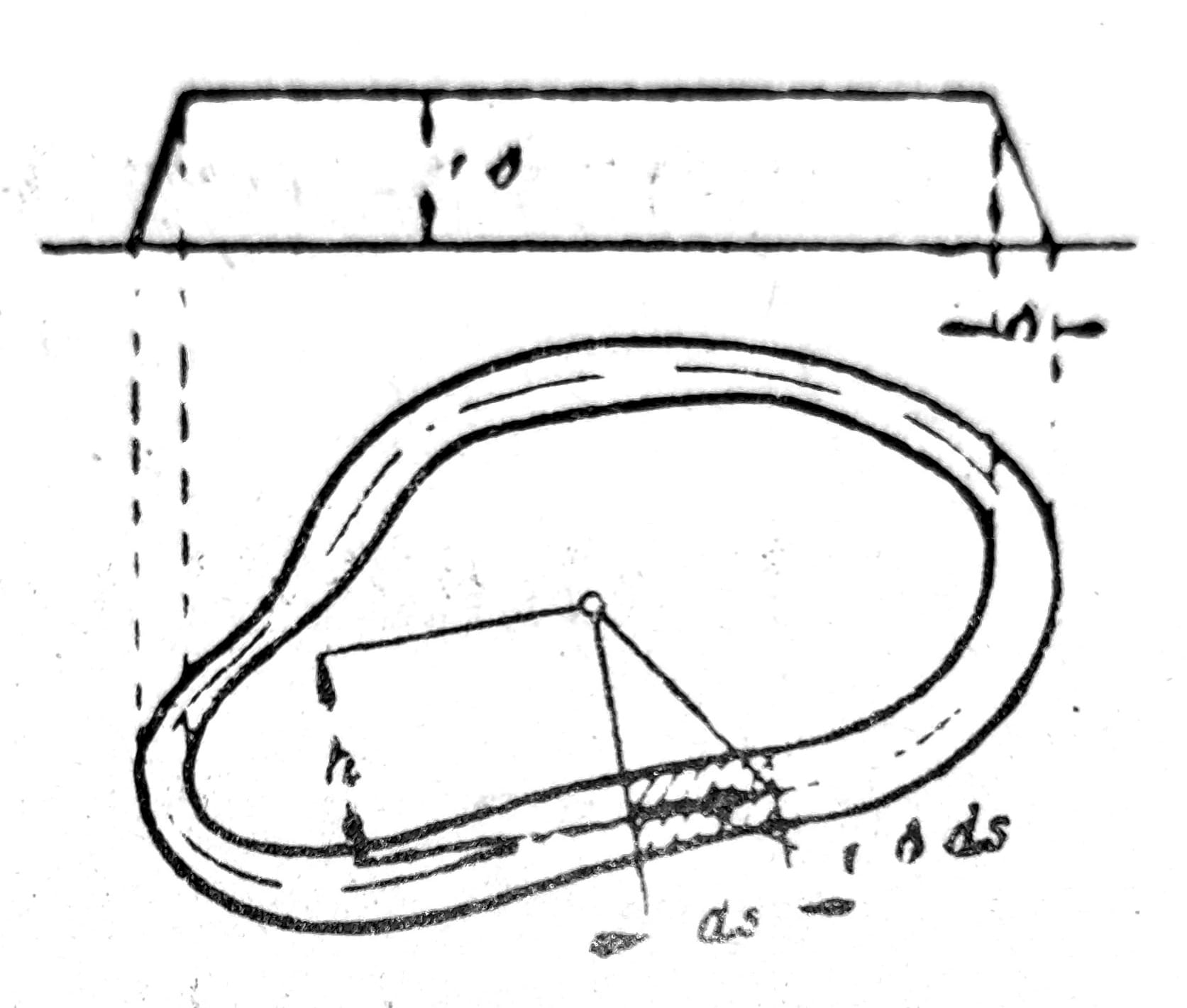
Sl. 8

Element površine t∙ds prima deo torzionog momenta

dM = t∙ds∙τ∙h,

tako da je ukupan moment

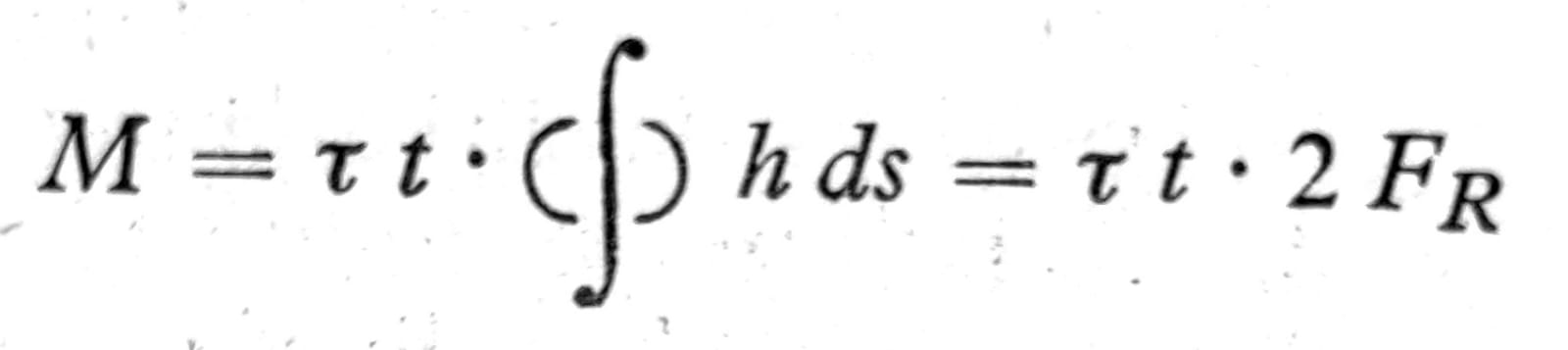
Jedn. 8

gde je F_R površina obuhvaćena srednjom linijom označenom crtama i tačkama na sl. 8. Odavde se dobija

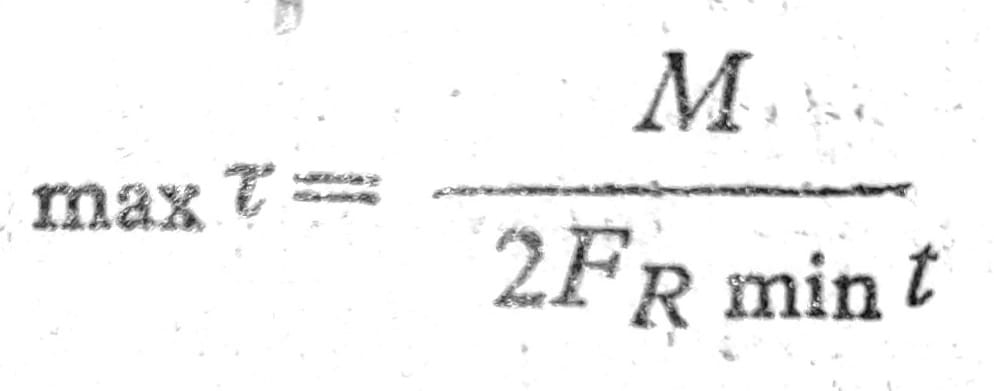
Jedn. 9 - Prvi Bredt-ov obrazac

Torziona krutost dobija se najjednostavnije kada se deformacioni rad izrazi s jedne strane preko momenta torzije i ugla torzije i s druge strane preko smičućih napona. Na taj način dobija se za element štapa dužine l

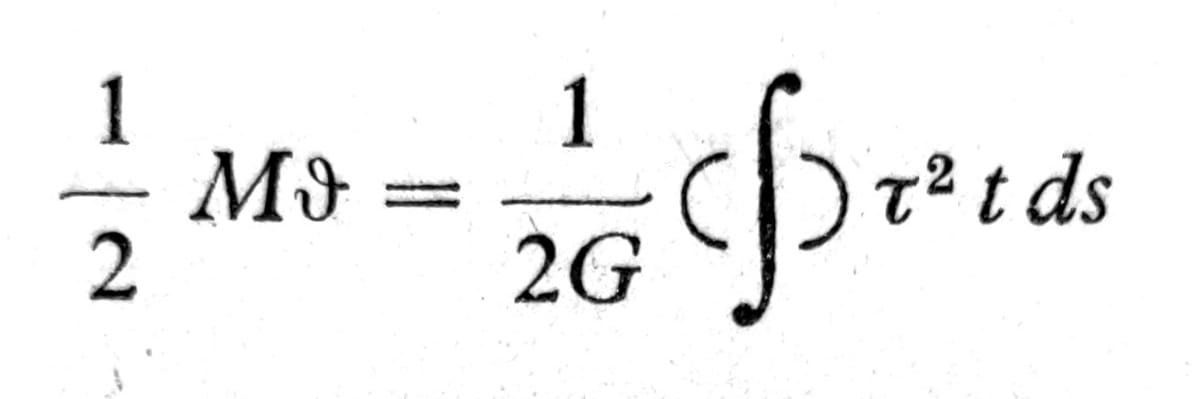
pa je, uvodeći vrednost za τ prema jednačini (8),

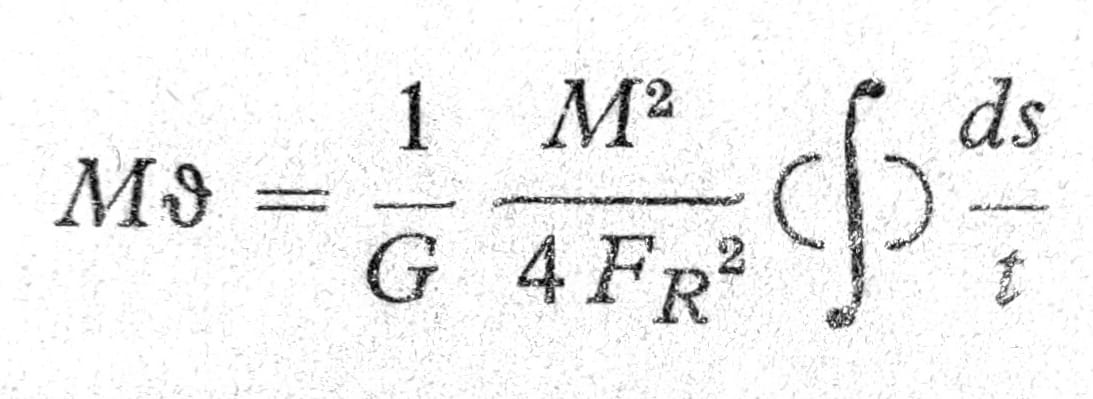
odnosno poređenjem sa jednačinom (2):

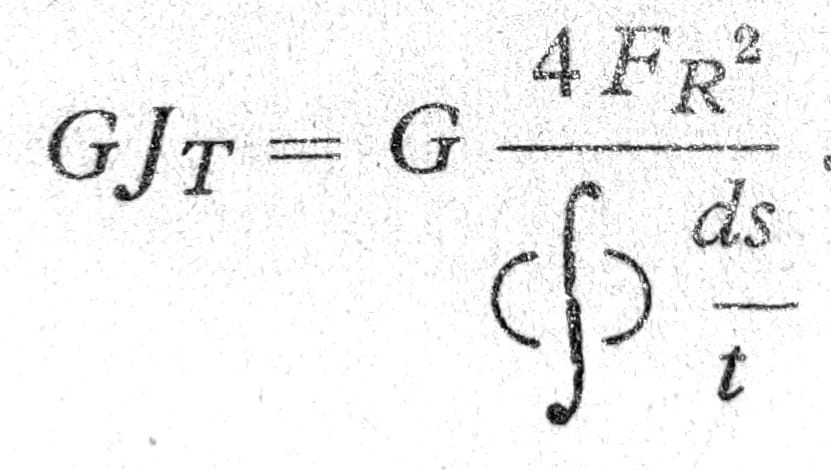
Jedn. 10

Ako je debljina zidova po celom obimu jednaka, tada je prosto (2. Bredt-ov obrazac):

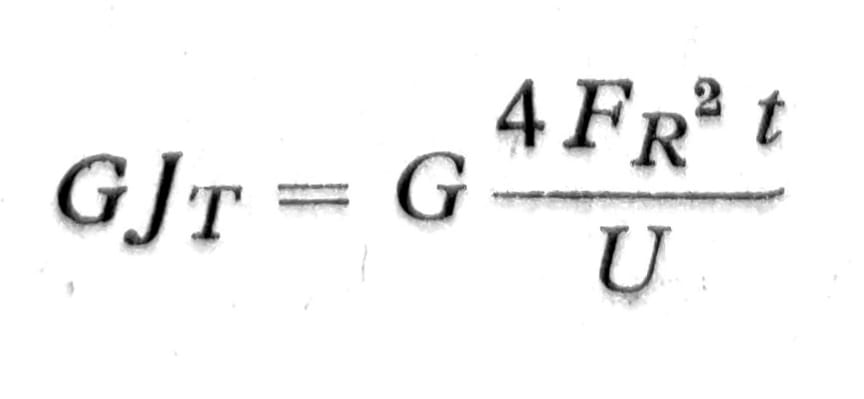
Jedn. 11

 

Pojava normalnih napona pri torziji usled krivljenja preseka

Osnovni pojmovi. Diferencijalna jednačina.

Komponentalna pomeranja u, jednačina (1b), određuje krivljenje preseka iz njihovih ravni. Kada je moment torzije konstantan, ovo krivljenje je u svim presecima isto i ne pojavljuju se normalni naponi σ_x.

U mnogim slučajevima krivljenje preseka koje bi trebalo da nastane na osnovu St. Venant-ove teorije nije moguće. Ako se torzioni moment menja u jednom preseku skokovito, na obe strane preseka bi nastalo krivljenje različite veličine, pri čemu bi bio narušen kontinuitet deformacije. Jedan kraj štapa može da bude tako uklešten da je na tome mestu krivljenje preseka potpuno isključeno. U takvim slučajevima treba izvršiti dopunu St. Venant-ove teorije. Pojavljuju se dopunski naponi σ_x u pravcu osovine štapa i dopunska sila smicanja T (smičući naponi T/t) u štapu koji su najveći u preseku gde je narušen kontinuitet deformacije i koji sa odstojanjem od ovog preseka opadaju eksponencijalno. Kod punih štapova i cevi ova teorija je složena, a dopunski naponi opadaju tako brzo da se njihovo određđivanje u većini slučajeva ne isplati. Kod štapova sa tankim zidovima otvorenog profila ova popravka je od velikog značaja i može se srazmerno lako izračunati.

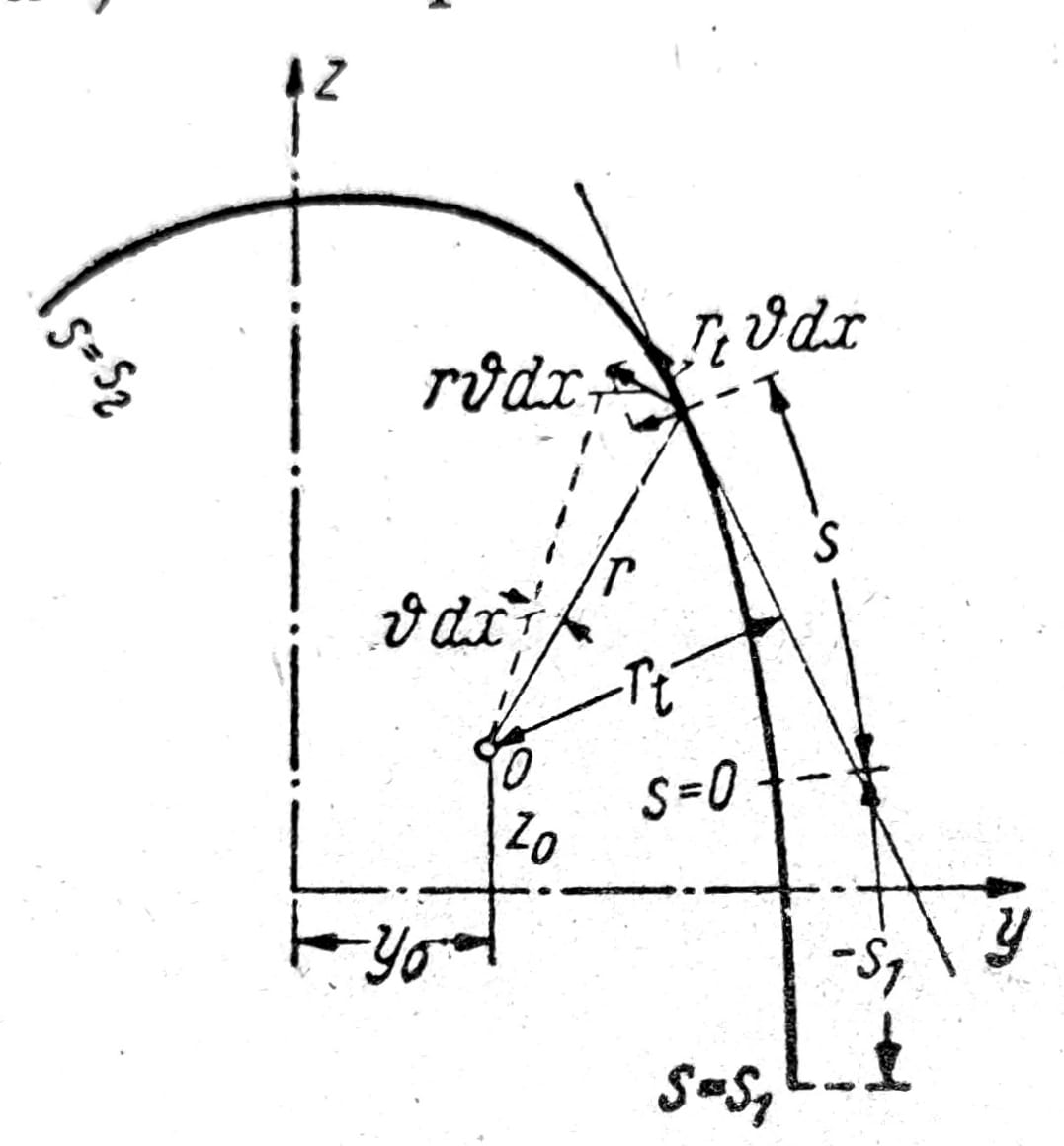
Sl. 9

Sl. 9 prikazuje liniju duž koje se seku srednja površina zida i ravan preseka (srednja linija preseka). O je centar relativnog obrtanja dva susedna preseka. Ako je njihovo odstojanje dx, ugao torzije ϑ dx, pa proizvoljna tačka srednje linije trpi pomeranje u ϑ dx. Ovo pomeranje ima komponentu r_t ϑ dx u pravcu tangente na presek, te je klizanje elementa srednje površine zida (uzimajući u obzir da je u=φϑ):

γ=ϑ (r_t + dφ/ds).

Kako je smičući napon u srednjoj površini zida nula, to mora da bude i γ=0, pa je zbog toga

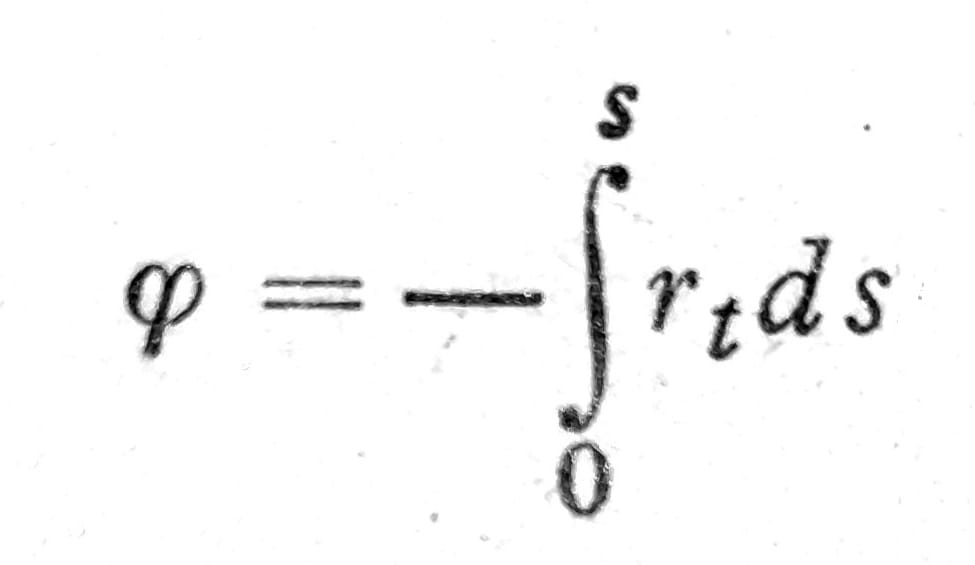
Ovaj obrazac sadrži tri proizvoljna parametra: početak od koga se računa dužina luka s i koordinate centra relativnog obrtanja O, od kojih zavisi r_t. Početak od koga se računa dužina luka s može se odabrati tako da je srednja vrednost krivljenja nula:

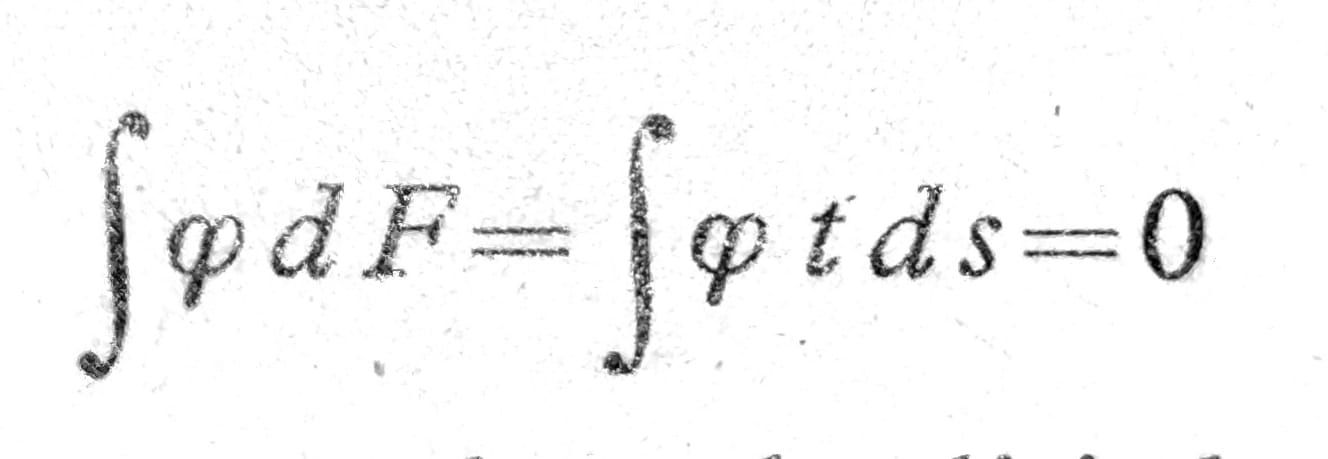
a koordinate centra O mogu se tako odrediti da i momenti usled krivljenja preseka budu nula:

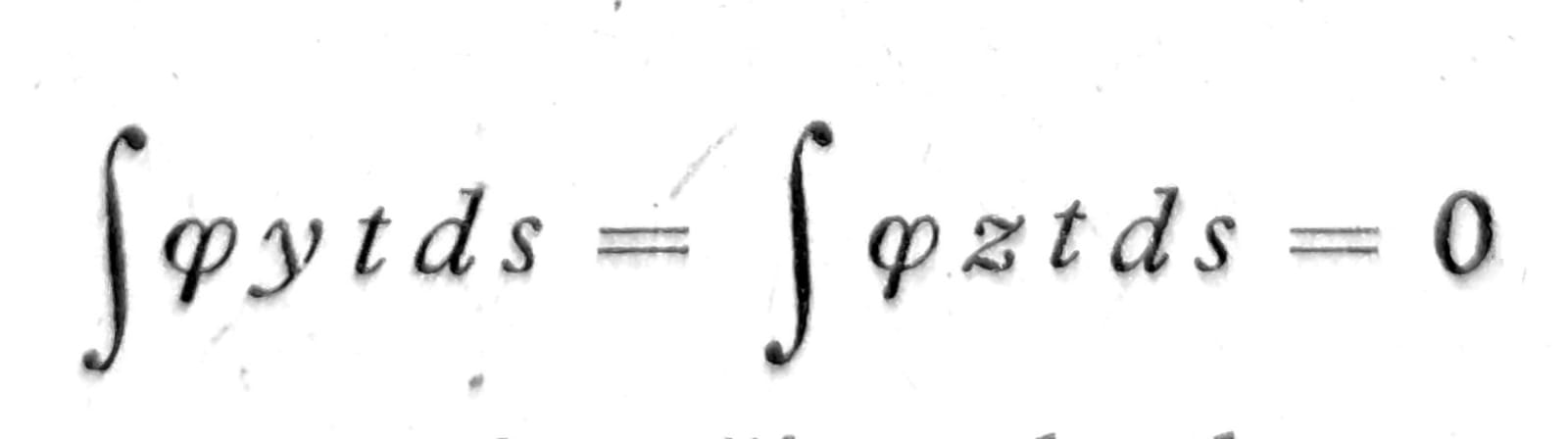
Može se pokazati da se na ovaj način određen centar obrtanja poklapa sa središtem smicanja koje je ovde opisano i definisano na drugi način.

Ako je krivljenje preseka opisano ovim obrascima potpuno ili delimično sprečeno, moraju se pojaviti normalni naponi σ_x u pravcu osovine štapa. Podrobnije proučavanje pokatuje da se može uzeti da su ovi naponi proporcionalni sa funkcijom krivljenja φ: σ_x=kφ, pri čemu φ zavisi samo od s, a k samo od x. Kako je prema Hooke-ovom zakonu:

σ_x = E∂u/∂x = Eφ dϑ/dx,   (12)

mora da bude k=E dϑ/dx. Normalni naponi σ_x nazivaju se naponi usled krivljenja preseka. S obzirom na jednačine iznad oni obrazuju u svakom preseku ravnotežni sistem sila, sistem sila usled krivljenja preseka.

Ukupni torzioni moment sastoji se iz dva dela: jedan od njih M₁=GJ_Tϑ proizilazi usled smičućih napona pri torziji koji daje St. Venant-ova teorija, a drugi M₂ nastupa usled krivljenja preseka:

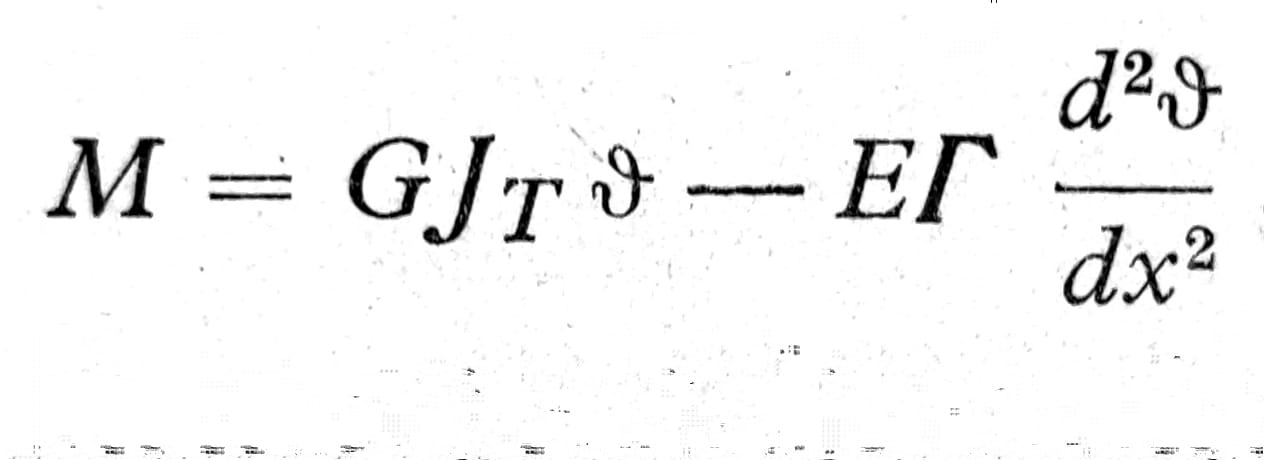
Jedn. 13

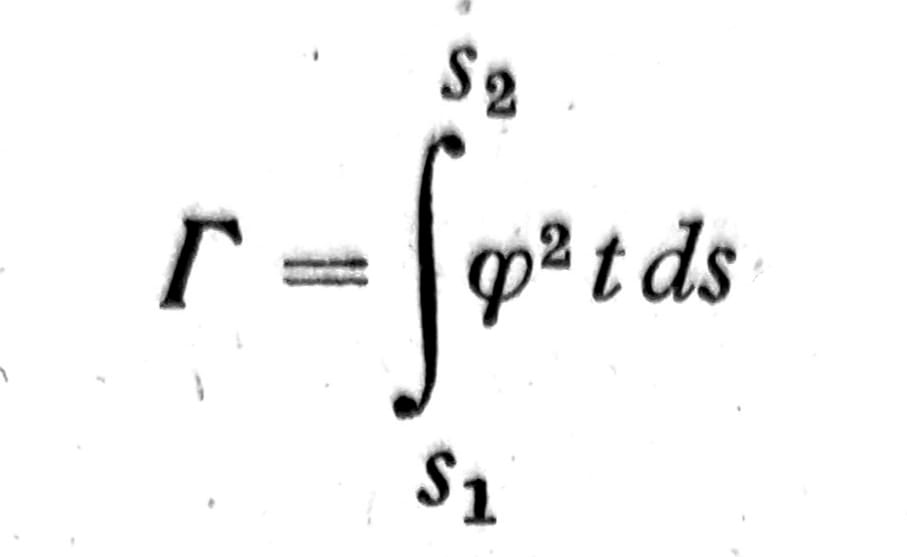
Kako moment M dat kao funkcija x, to ovaj izraz predstavlja diferencijalnu jednačinu za ugao torzije ϑ. Kada se ova jednačina reši, mogu se sračunati M₁ i M₂, a time i svi naponi i deformacije.

Rešenje. Primene.

Kada je moment torzije M konstantan, opšte rešenje jednačine (13) je:

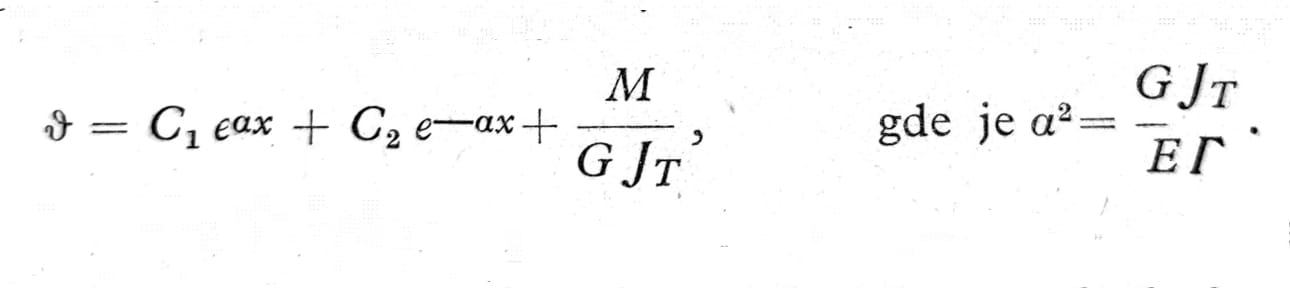
Integracione konstante C₁, C₂ moraju se odrediti iz dva granična uslova.

a) Kruto uklješteni kraj x=0 (sl. 1). Na ovome kraju je u≡0, pa je na osnovu jednačine (1b) ϑ=0. Ako je štap vrlo dugačak (αl>>1), tada je C₁=0 i C₂= -M/GJ_T. Kod kratkih štapova na pojavu napona usled krivljenja preseka utiče stanje na desnom kraju štapa. Ako na tome mestu krivljenje preseka nije sprečeno, tu će biti σ_x≡0 i dϑ/dx=0. Odavde se dobija

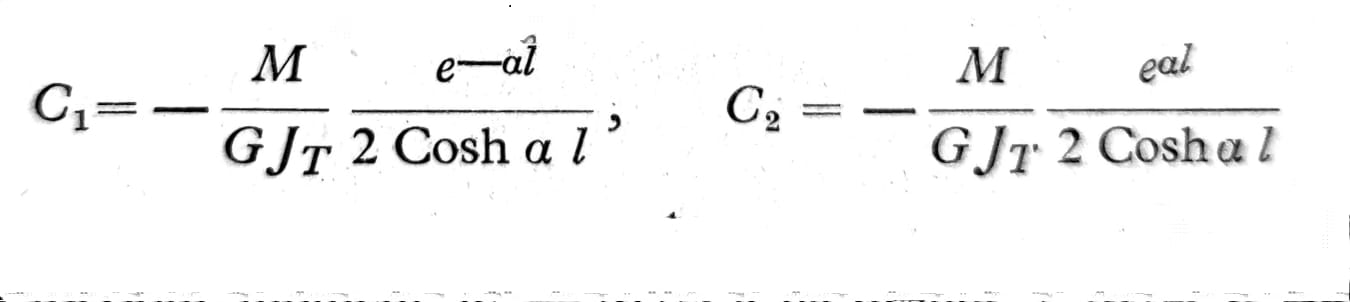
b) Simetrično opterećenje na torziju prema sl. 10. Na levoj polovini štapa torzioni moment je -M/2, a na desnoj +M/2. U slučaju slobodno torzije preseci levo i desno od sredine štapa iskrivili bi se u suprotnom smeru, prema tome kontinuitet deformacije ne bi bio očuvan. Zbog toga na mestu x=0 celokupni moment torzije mora da se prenese preko napona koji nastupaju usled krivljenja preseka, te je zbog toga u ovome preseku M₁=0 i prema tome ϑ=0. Na ovome mestu deluje sistem sila koji obezbeđuje da presek ostaje ravan, iako se preseci koji leže dalje od sredine štapa krive. Ako se osim toga zahteva da su na krajevima štapa naponi σ_x≡0, dobija se još jedan granični uslov za svaku polovinu štapa, pa je za desnu polovinu

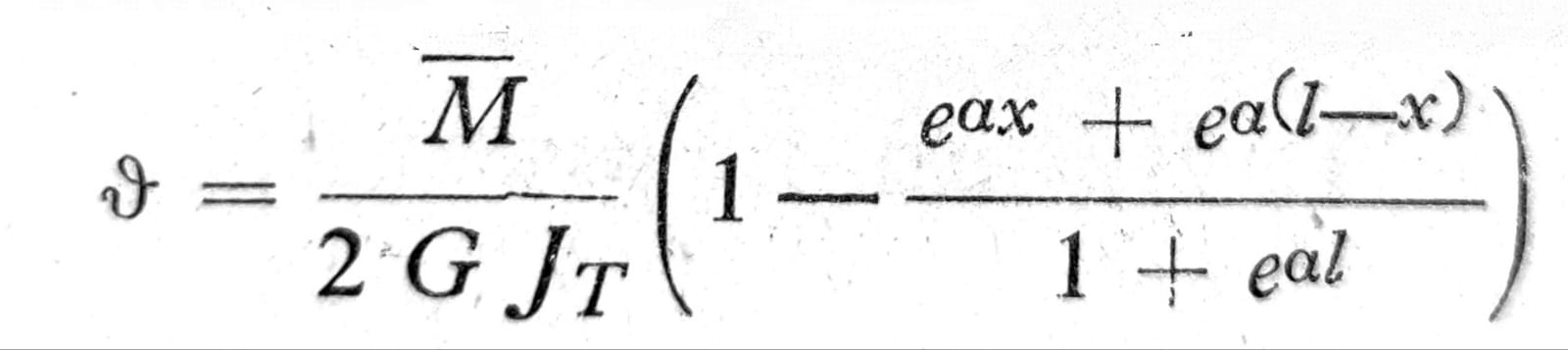
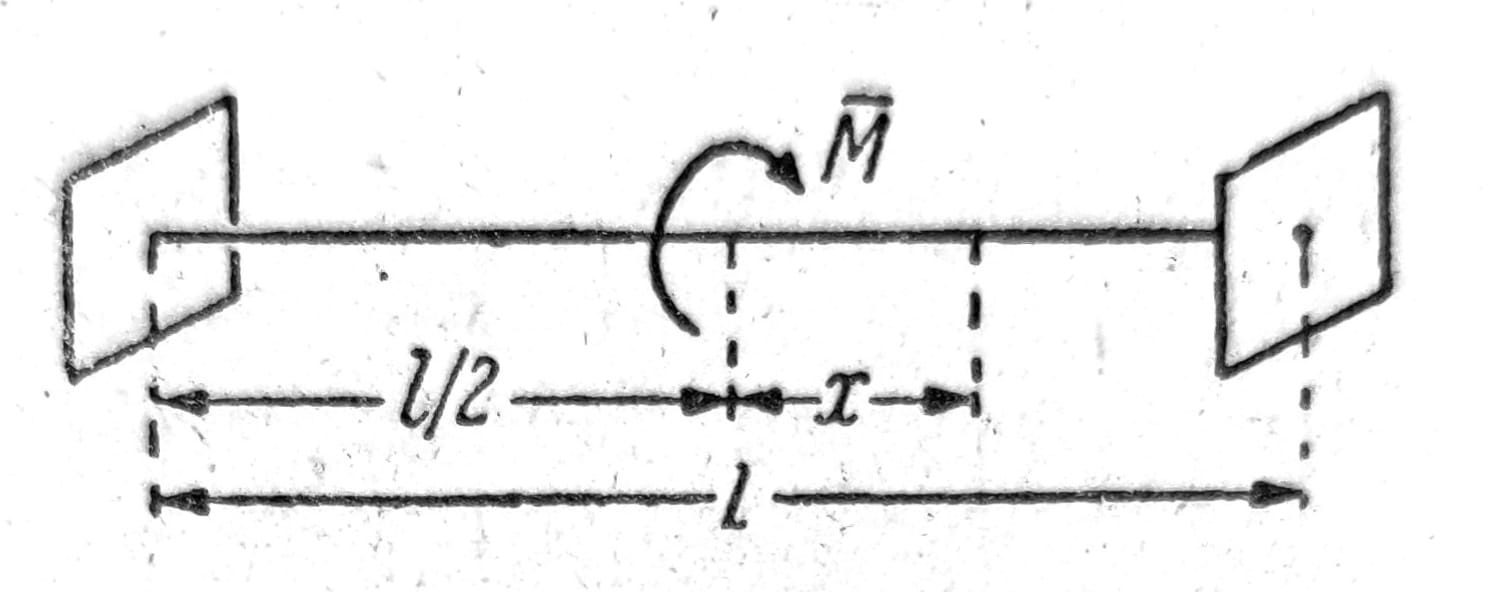
Sl. 10

c) Spoljni moment M na proizvoljnom mestu (sl. 11). U ovom slučaju rešenje ϑ za oba dela štapa moda se posebno napisati, pa se pojavljuju ukupno četiri konstante C₁, C₂, C₃, C₄. Osim toga nepoznati su i momenti torzije M_a, M_b. Na raspoloženju je šest jednačina: uslov neprekidnosti za ϑ (izražen po u) i za dϑ/dx (izražen po σ_x) na mestu delovanja tereta, po jedan uslov na svakom kraju štapa (npr. kruti uklještenje ϑ=0, ili neometano krivljenje, dϑ/dx=0), uslov ravnoteže po momentima -M_a+M_b=M i najzad uslov da se krajnji preseci prema drugome ne obrću: ∫ ϑdx = 0.

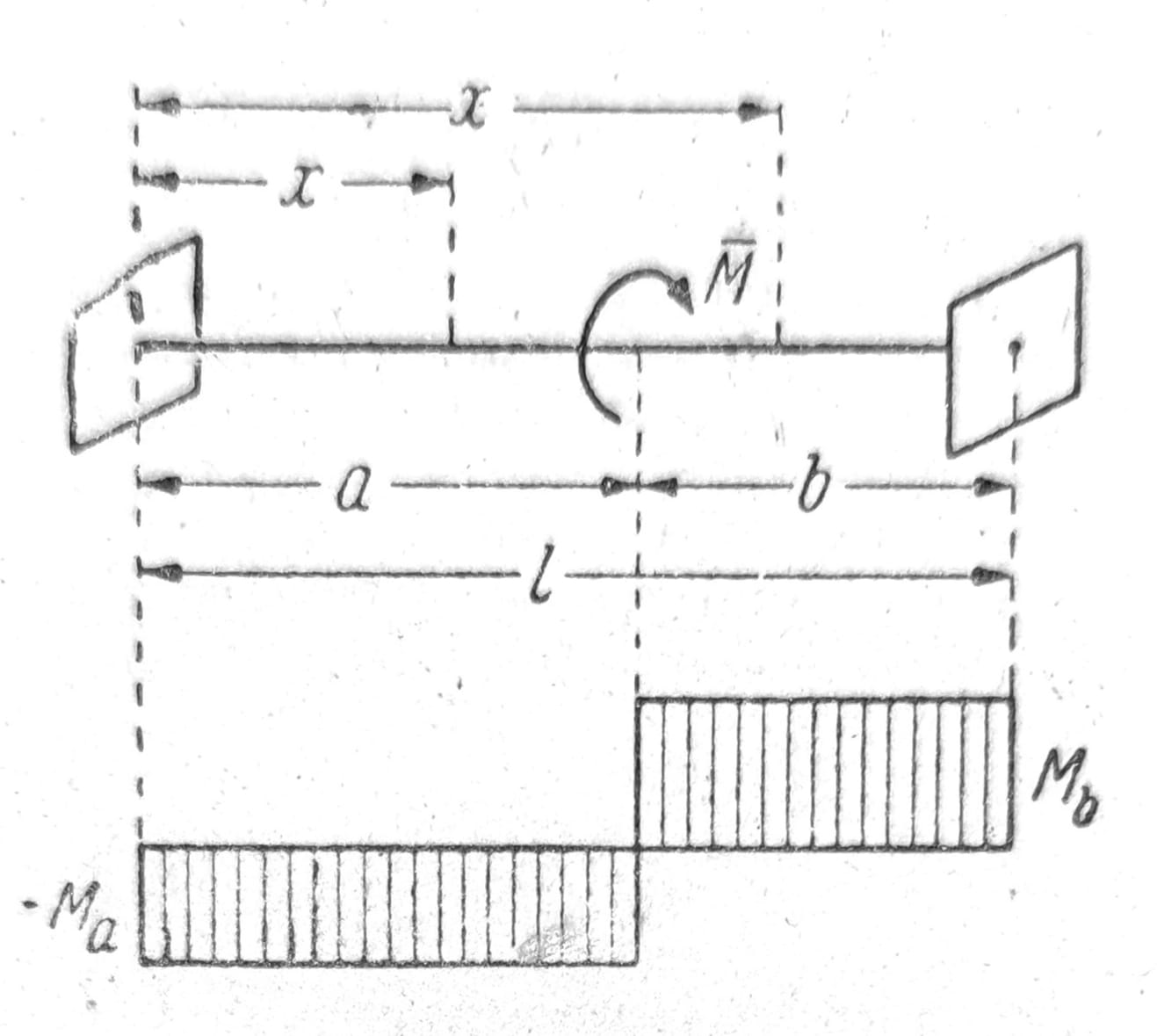
Sl. 11