Prosto savijanje i savijanje sa normalnom silom

Normalni naponi kod pravih štapova i štapova sa malom krivinom

Definicija presečnih sila

Neka je prav štap opterećen silama proizvoljnog pravca, o kojima se jedino pretpostavlja da sve leže u jednoj ravni (ravan sila) koja prolazi kroz osovinu štapa (linija koja spaja težišta poprečnih preseka).

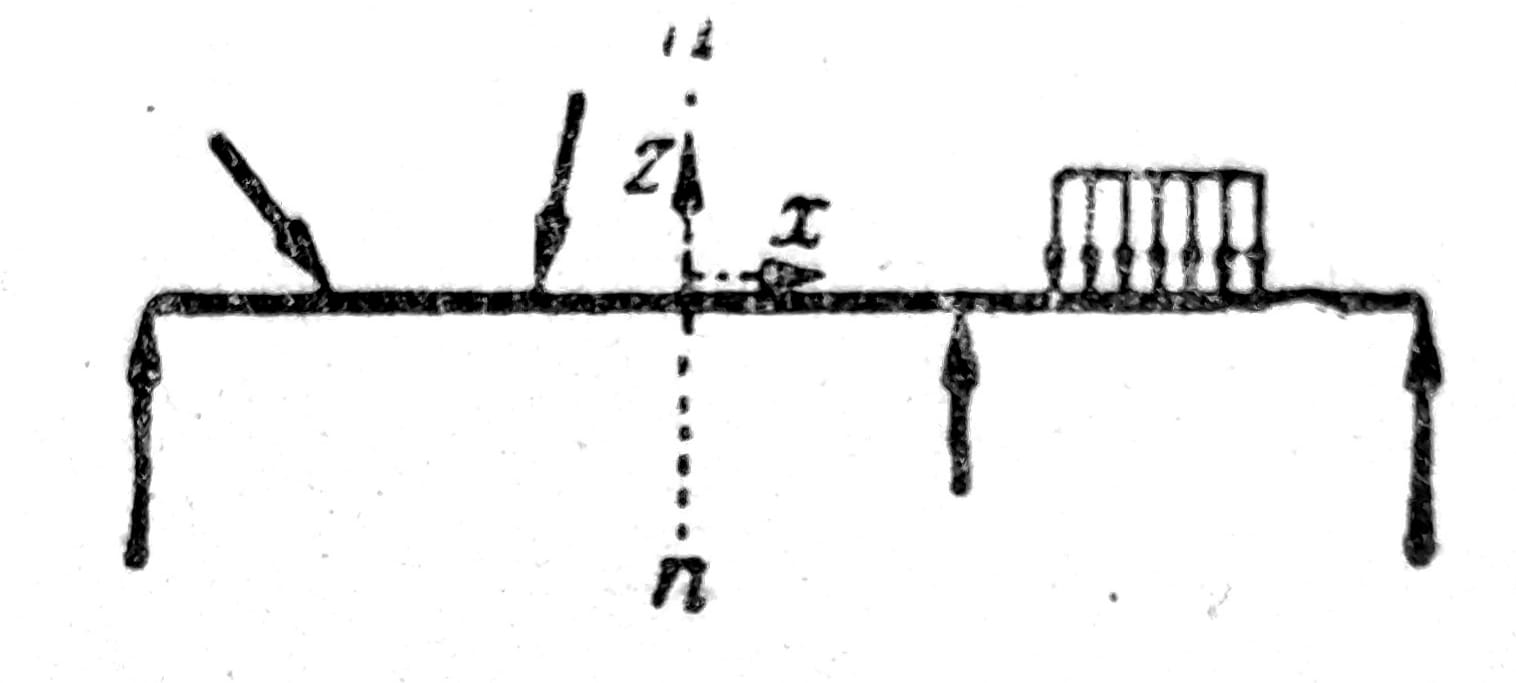
Sl. 1

Da bi se izračunali naponi koji deluju u nekom poprečnom preseku n – n (sl. 1), potrebno je da se poznaje sila koja se preko ovog preseka prenosi sa jednog dela štapa na drugi. Ona je očigledno po veličini i položaju jednaka rezultanti svih sila koje napadaju jedan deo štapa. Ova rezultanta se razlaže na komponente u koordinatnom sistemu čija se x-osovina poklapa sa osovinom štapa, a z-osovina linija duž koje ravan poprečnog preseka seče ravan sila. Komponenta u pravcu osovine z naziva se transverzalna sila Q ili Q_z i kod proste grede smatra se pozitivnom ako levo od preseka ima smer naviše, a desno naniže.

Kad je štap kriv, koordinatne osovine x i z imaju u svakom preseku drugi pravac i to uvek tako da je x-osovina tangenta na osovinu štapa. Ako se ravan u kojoj leži osovina štapa ne poklapa sa ravni sila, ili ako je osovina štapa prostorna kriva, rezultanta sila levo od preseka ima i treću komponentu, transverzalnu silu Q_y. Sa N, Q_z i Q_y određene su veličina i pravac sile koja se prenosi preko preseka, ali ne i njen položaj. Za ovo je potrebno da budu poznati i njeni momenti u odnosu na koordinatne osovine. U slučaju ravnog savijanja dovoljno je da bude poznat moment savijanja M ili M_y. U najopštijem slučaju pojavljuje se još jedan moment savijanja M_z i moment oko x-osovine, M_x.

Šest sila i momenata definisanih u prethodnom izlaganju obuhvaćeni su zajedničkim nazivom „presečne sile“. Njihovo određivanje je jedan od osnovnih zadataka statike građevinskih konstrukcija.

Između neprekidno podeljenog opterećenja p (dimenzija: sila na jedinicu dužine), transverzalne sile Q i momenta savijanja M postoji u slučaju ravnog savijanja jednostavan odnos. Naime, iz uslova ravnoteže jednog elementa štapa (sl. 2) dobija se

dQ + p dx = 0,

dM = Q dx;

dakle

Q = dM/dx, 

p = - dQ/dx = - d²M/dx².        (1a, b)

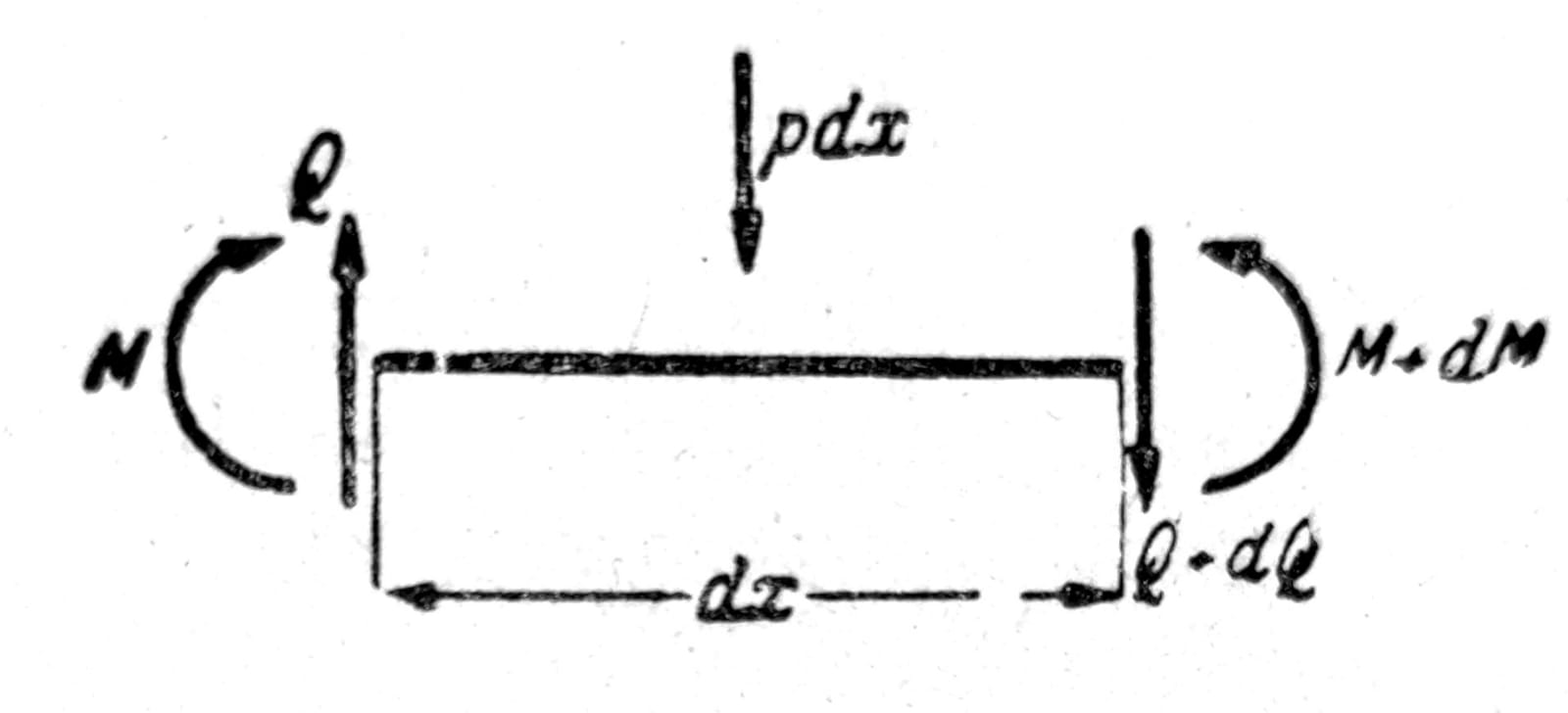
Sl. 2

 

Raspodela normalnih napona

Ako je štap opterećen samo aksijalnom silom, u preseku se pojavljuje samo ravnomerno raspoređeni normalni napon σ (zategnuti, odn. pritisnuti štap). Ako se uz to pojavljuje moment savijanja, ovi naponi moraju na neki način da budu neravnomerno raspoređeni, tako da njihova rezultanta više ne prolazi kroz težište preseka. Da bi se odredio ovaj raspored, tehnička teorija savijanja ne polazi od strogog rešenja osnovnih jednačina, nego zamenjuje jedan deo ovih jednačina plauzibilnom pretpostavkom koja je u jednom naročito jednostavnom slučaju ujedno i strogo ispunjena. Ovaj specijalni slučaj je savijanje pravom prizmatičnog štapa bez delovanja transverzalnih sila (sl. 3). Svi elementi štapa koji su dovoljno udaljeni od njegovih krajeva trpe istu deformaciju, odakle neposredno sleduje da osovina štapa prelazi u kružni luk i da sve ravni poprečnih preseka koje su prvobitno bile upravne na osovinu štapa prilikom deformacije ostaju ravne, jer je svaka od njih ravan simetrije za susedne delove deformisanog štapa. Prirodno se nameće pretpostavka da poprečni preseci ostaju približno ravni i kada moment savijanja i poprečni presek štapa nisu konstantni, već se duž štapa postepeno menjaju. Ova pretpostavka koja se naziva Navier-ova hipoteza leži u osnovi teorije savijanja.

Sl. 3

Veličina normalnih napona

Kada se savije prav element grede, jedan deo njegovih „vlakana“, tj. materijalnih linija paralelnih osovini štapa, isteže se, dok se drugi deo skraćuje (sl. 4). Između ova dva dela leže neutralna vlakna z=0, čija se dužina prilikom savijanja ne menja. Neka je poluprečnik krivine ovih vlakana u savijenom stanju ϱ i neka on leži u x-z ravni. Iz sl. 4 može se pročitati

Δ dx/z = dx/ϱ

i odatle proračunati dilatacija vlakana na odstojanju z od neutralne osovine, koja iznosi

ε = Δ dx/dx = z/ϱ

pa je na osnovu Hooke-ovog zakona napon

σ = Ez/ϱ   (2)

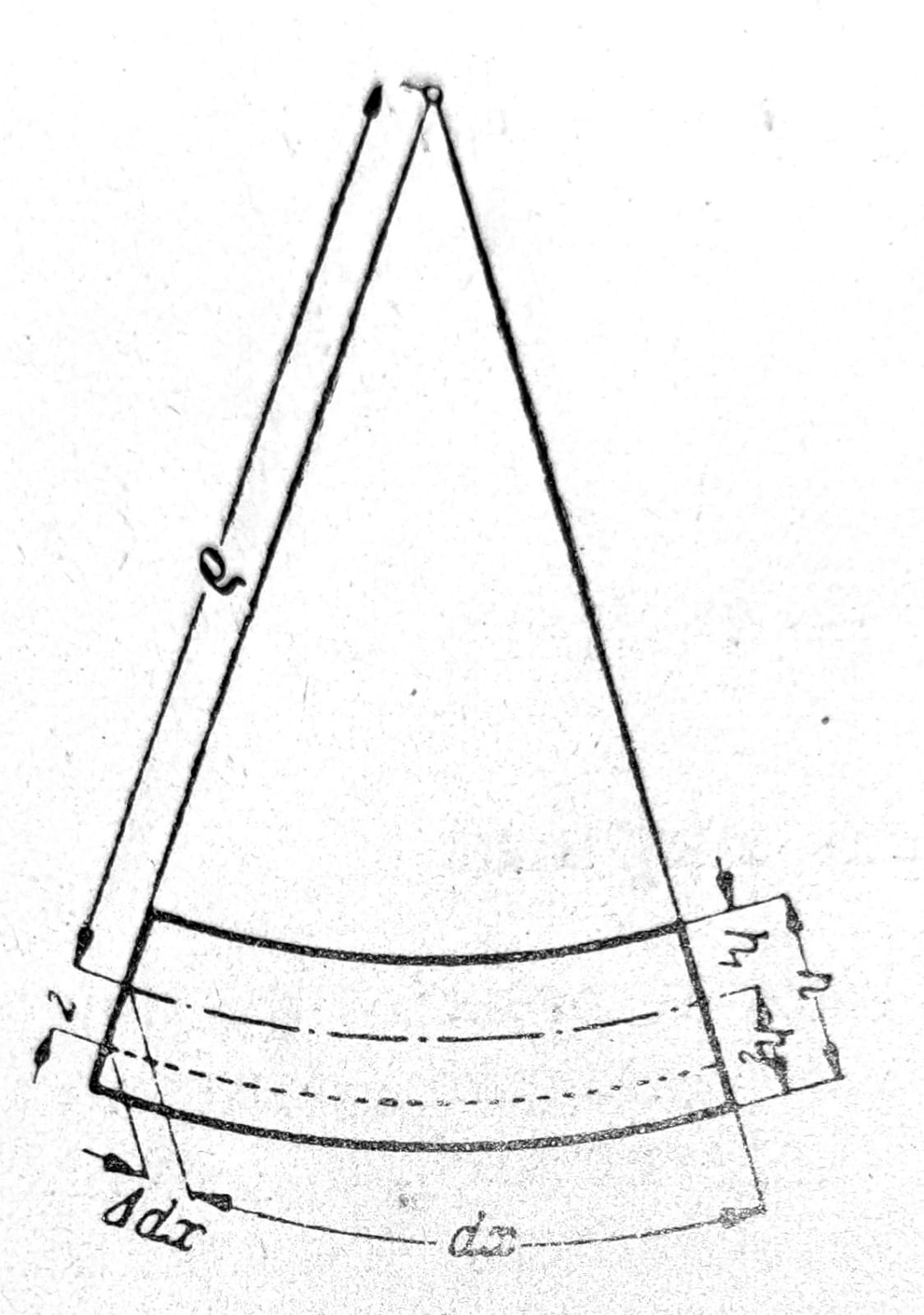
Sl. 4

Ovaj napon je proporcionalan odstojanju od neutralnih vlakana. Takav rezultat je vezan za pretpostavku da su pre deformacije sva vlakna elementa štapa bila podjedake dužine, tako da je štap prvobitno bio prav, ili bar sa tako malom krivinom da se uticaj krivine može zanemariti. Prava duž koje se seku neutralni sloj i ravan preseka naziva se neutralna osovina. Nju usvajamo za y-osovinu (sl. 5). Položaj neutralne osovine u poprečnom preseku dobija se iz uslova ravnoteže sila u pravcu x-osovine: ako je normalna sila N=0 (savijanje bez normalne sile), tada mora i rezultanta unutrašnjih sila izražena putem normalnih napona u preseku da bude ravna nuli:

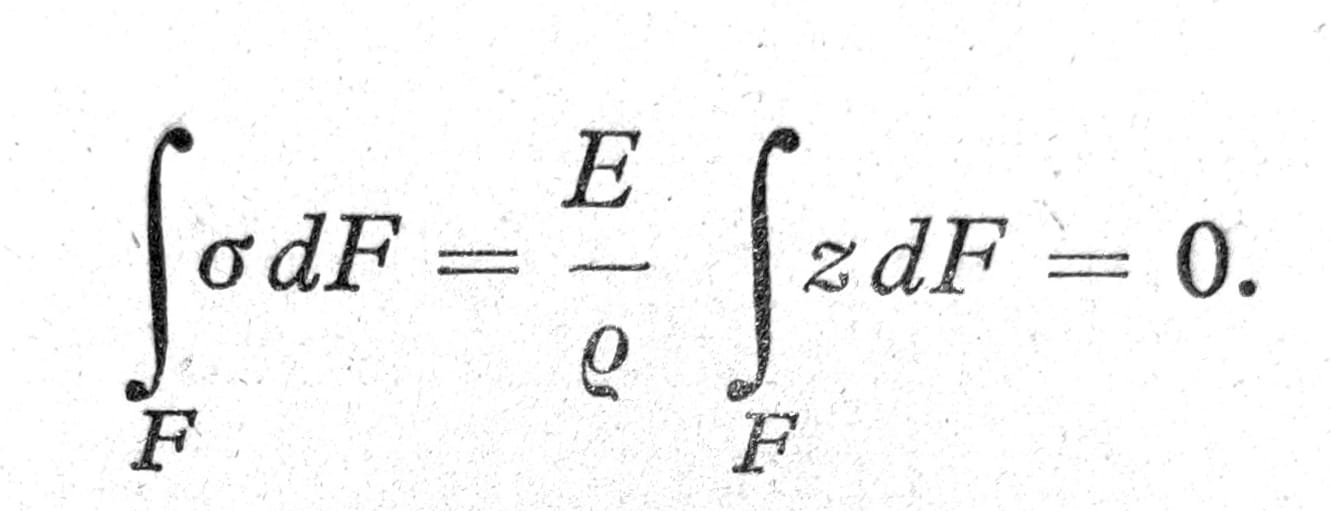
Integral na desnoj strani je statički moment površine u odnosu na y-osovinu. Da bi on bio jednak nuli, ova osovina mora da bude jedna od težišnih osovina.

Moment M koji izaziva deformaciju ima u odnosu na osovine y i z u ravni preseka (sl. 5) komponente:

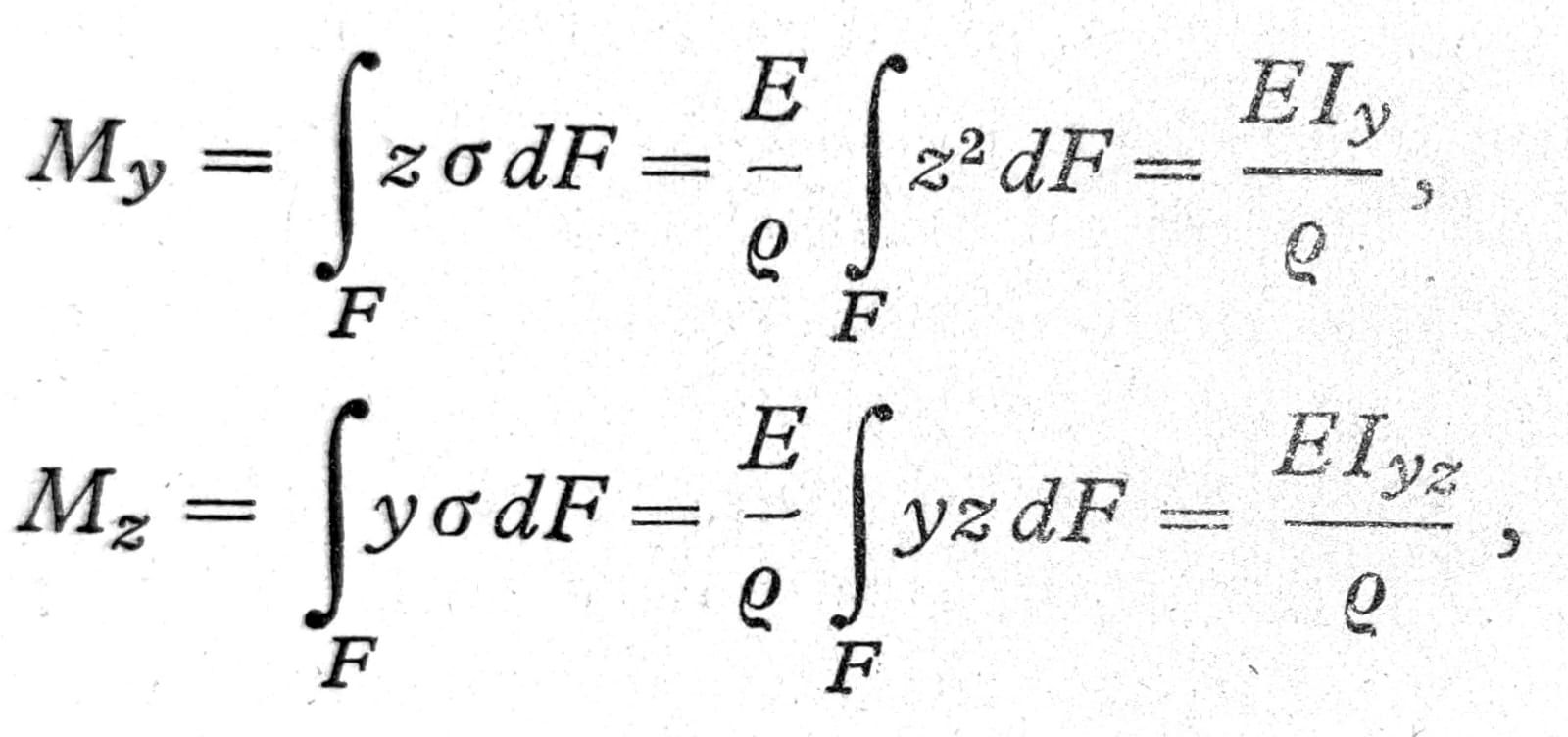Jedn. (3)

pri čemu su I_y, I_yz ekvatorijalni i centrifugalni moment inercije preseka u odnosu na označene osovine.

Najvažniji je specijalan slučaj kada je M_z=0. Ovaj slučaj nastupa kada je I_yz=0, tj. kada su y i z glavne osovine inercije preseka. To znači da je ravan savijanja koja je ovde usvojena sa x-z-ravan poklapa sa ravni u kojoj deluje moment savijanja M=M_y, tj. sa ravni sila.

Sl. 5

Ako se iz jednačina (2) i (3) eliminiše E/ϱ, dobija se obrazac za određivanje napona pri ravnom savijanju (I_y=I):

σ = M/I * z   (4)

za ivične tačke 1 i 2 posebno je:

σ₁ = M/I * h₁ = M/W₁, σ₂ = - M/I * h₂ = - M/W₂.   (5)

Veličine W_1,2 = I/h_1,2 (dimenzija: dužina na treći) nazivaju se otporni momenti. Ako je horizontalna težišna osovina ujedno i osovina simetrije preseka, tada je W₁ = W₂, pa su ivični naponi po apsolutnoj veličini jednaki.

Elastična linija

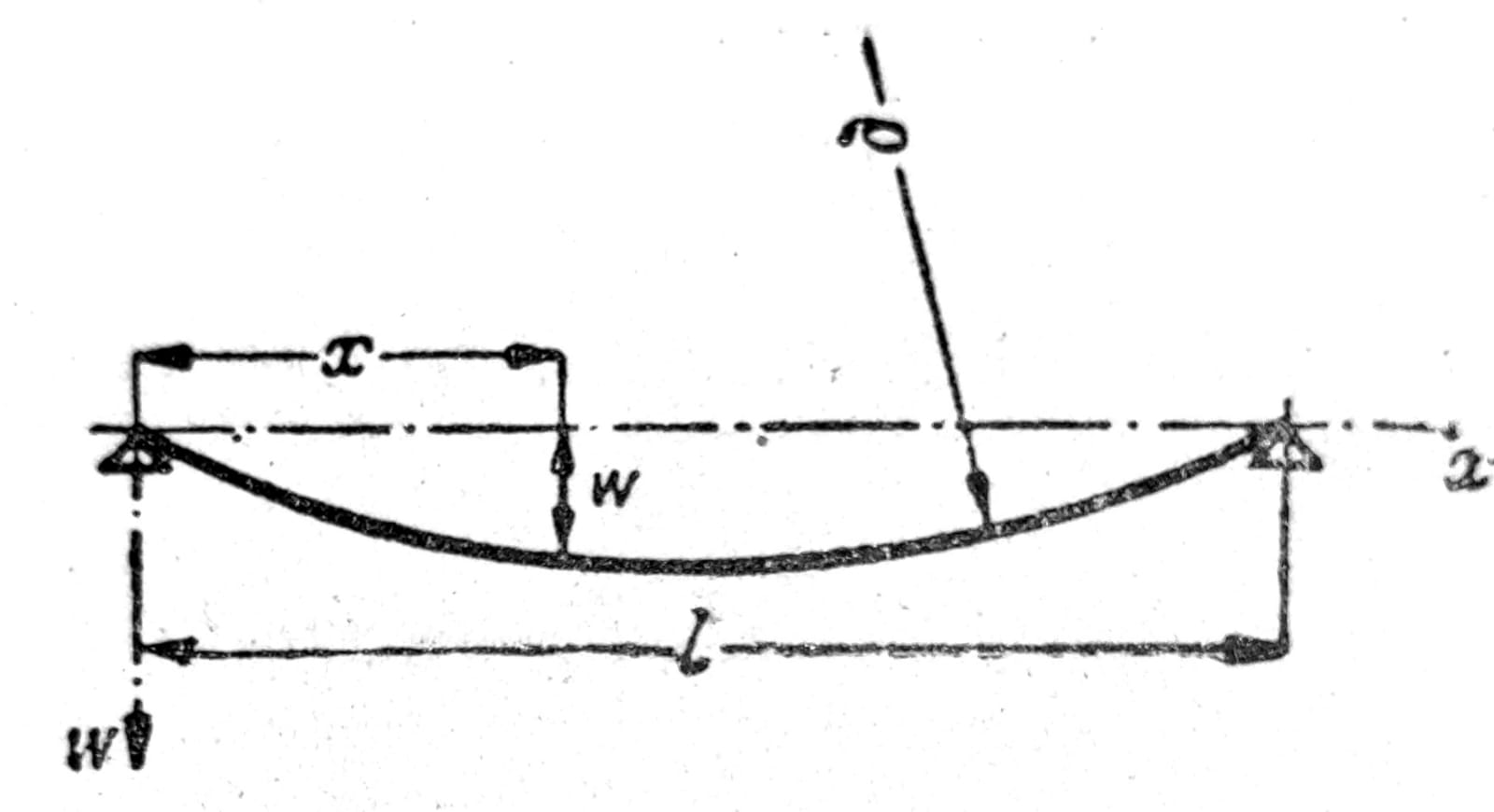
Sl. 6

Važnost napred navedenih obrazaca vezana je za Hooke-ov zakon. To zahteva da je σ << E, dakle prema (2) h << ϱ. Savijanje ipak sme da bude toliko da je ϱ istog reda veličine kao i dužina štapa l. Kod savijenih štapova koji dolaze u obzir u građevinarstvu ovaj slučaj ne nastupa; uvek je ϱ znatno veće od l i prema tome ugib w << l (sl. 6). Tada približno važi:

1/ ϱ = - d²w/dx² = -w’’

i na osnovu (3):

w’’ = - M/EI.

Ova jednačina i uslov ravnoteže (1b) čine sistem diferencijalnih jednačina savijenog štapa. One se eliminacijom mogu svesti na jednu jednačinu četvrtog reda:

w^IV = + p/EI

ili, u slučaju da je moment inercije promenljiv:

(EIw’’)’’ = +p.

Iz njih se integracijom može naći oblik elastične linije kada je dato opterećenje p=p(x) i kada su za svaki slučaj štapa poznata dva granična uslova. Od ovih bar dva moraju da se odnose na deformaciju. Za pojedinosti v. članak Statika građevinskih konstrukcija.

Jezgro preseka

Ako neutralna osovina seče poprečni presek, ona ga deli na zonu zatezanja i zonu pritiska. Kod materijala sa malom čvrstoćom na zatezanje nameće se pitanje gde treba da napada sila pritiska, ako u poprečnom preseku ne sme nigde da dođe do zatezanja. Položaj napadne tačke sile tada je ograničen na oblast koja se naziva jezgro preseka. Granica jezgra je očigledno geometrijsko mesto tačaka, čije neutralne osovine tangiraju poprečni presek po obimu. Ovim je ujedno data i njegova konstrukcija.

Odstojanje granice jezgra od težišta, izmereno u bilo kom pravcu, označićemo sa k indeksom koji odgovara tom pravcu. Za glavne osovine inercije prema jednačini

σ = N/F + M_z/I_z y + M_y/I_y z  (6)

izrazi su sledeći:

k_y = i²_z / e_y,      k_z = i²_y / e_z.   (7)

Za kružni poprečni presek poluprečnika r odstojanje jezgra je k = r/4, a za kružni prsten (poluprečnici: spoljni R, unutrašnji r) k = (R² + r²) / 4R.

Za pravougaonik (sl. 7) je k_y = 1/6 b, k_z = 1/6 h. Dakle, pri opterećenju pravougaonog preseka u jednoj od ravni simetrije (ali samo tada) dovoljno je da rezultanta napada u srednjoj trećini visine ili širine poprečnog preseka, pa da naponi u preseku imaju isti znak.

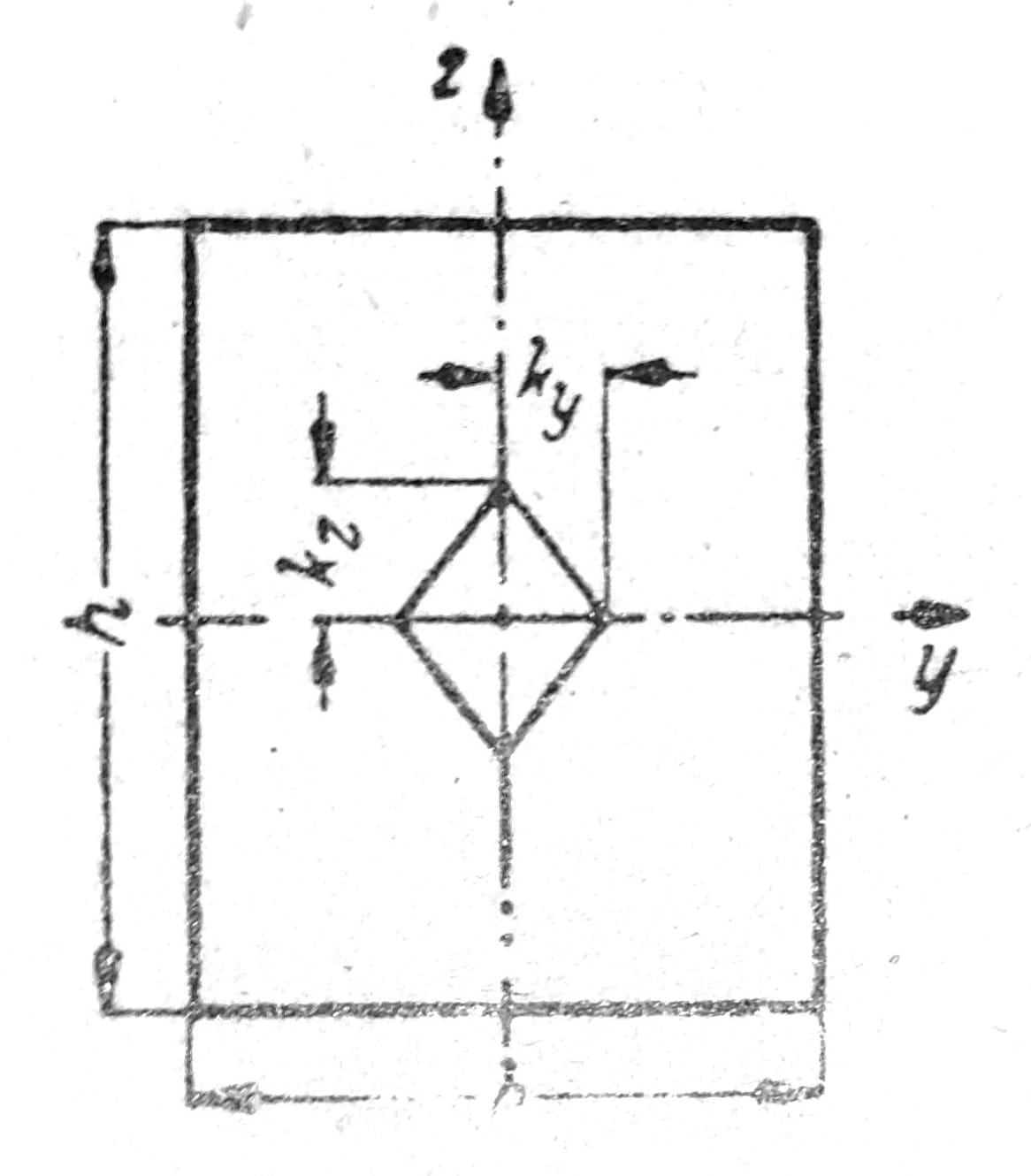
Sl. 7

Savijanje u plastičnoj oblasti

Kada je u ivičnim vlaknima savijenog štapa dostignuta granica tečenja, njegova nosivost time još nije iscrpljena, jer dok se spoljna vlakna plastično deformišu pri konstantnom naponu, u delovima koji leže bliže neutralnoj osovini, gde granica tečenja još nije dostignuta, napon se povećava, pa se time povećava i moment savijanja koji presek može da primi.

Ako je poznat tačan tok dijagrama napona i deformacija, proces se za svostruko simetričke preseke (visine h) može lako računski pratiti na taj način što se, pod pretpostavkom da preseci ostaju ravni, iz dijagrama napona i deformacija odredi raspored napona σ usled savijanja koji odgovara nekoj usvojenoj dilataciji krajnjih vlakana ε_r i odatle integriranjem odredi moment savijanja. Ako se ovo sprovede za različite ε_r i s druge strane sračuna odgovarajuća krivina linije ugiba w’’ = 2 ε_r / h, dobija se niz tačaka kroz koje se može provući linija koja daje vezu između momenta savijanja i krivine M = M(w’’); ova veza više nije linearna, a kada je ona poznata moguće je grafičkom integracijom odrediti liniju ugiba koja odgovara datom rasporedu momenata. Ako je presek nesimetričan, račun postaje složeniji, utoliko što se za svako ε_r mora još odrediti i položaj neutralne osovine.

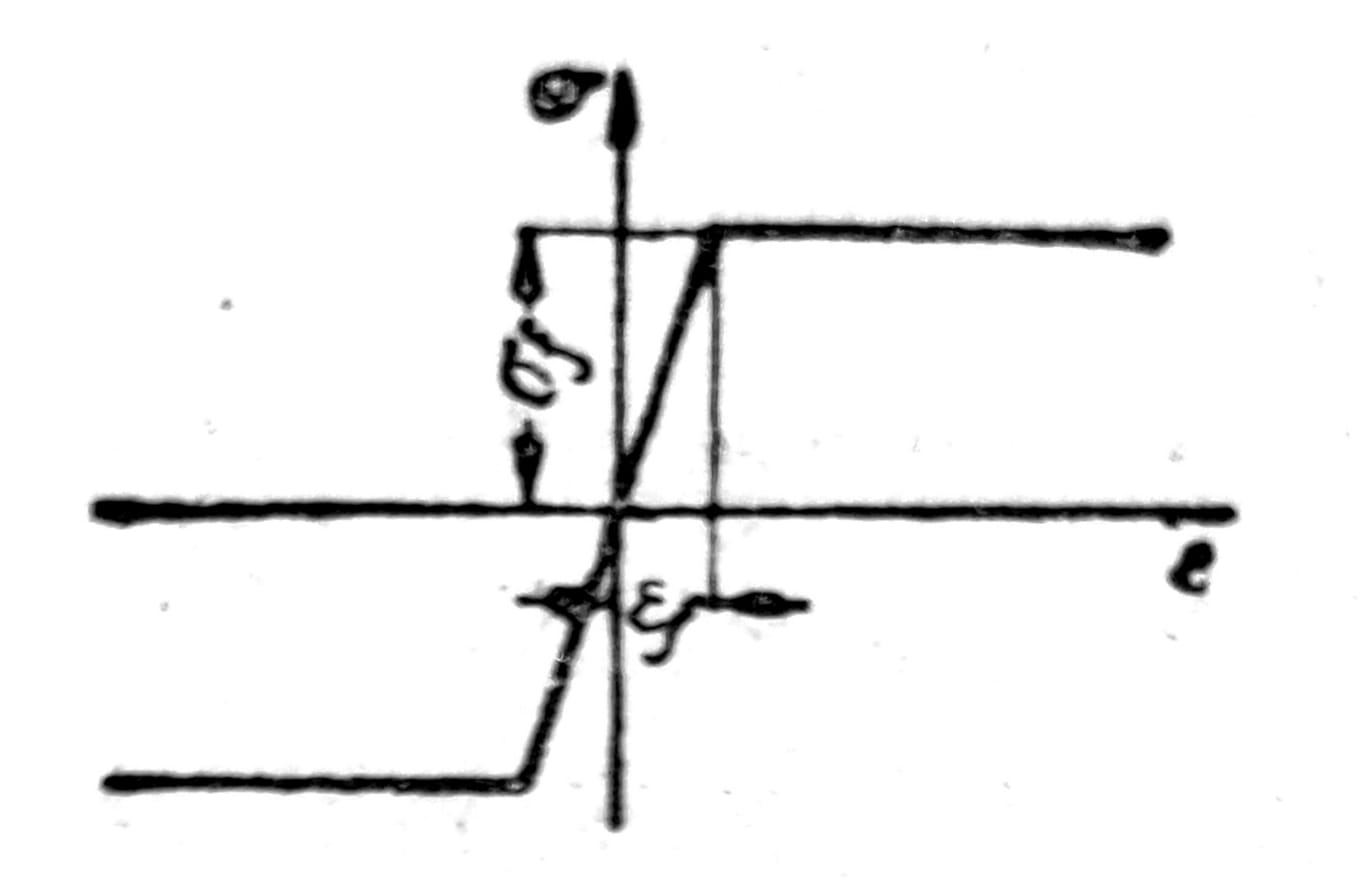
Sl. 8

Račun se u izvesnoj meri uprošćava ako se osim simetrije preseka pretpostavi i uprošćena veza između napona i dilatacija prema sl. 8. Tada naponi usled savijanja po prekoračenju granice tečenja imaju raspored prikazan na sl. 9 i moment savijanja je:

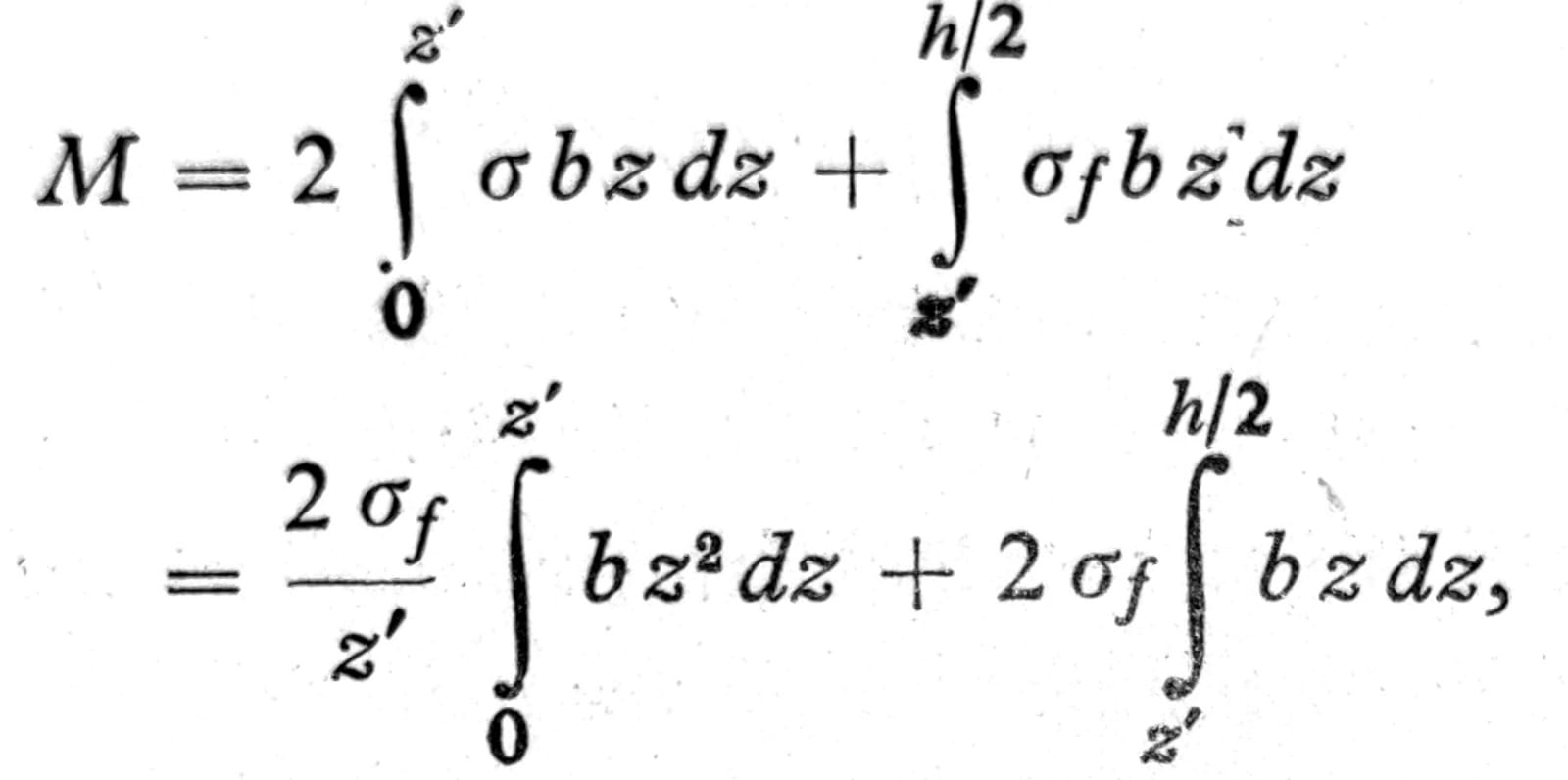
pa se krivina linije ugiba dobija kada se jednačina (2) primeni na deo preseka čiji su naponi u elastičnoj oblasti w’’ = σ_f / Ez’. Ako je poznat oblik preseka za svako usvojeno z’ integrali se mogu izračunati. Npr. za najprostiji slučaj pravougaonog poprečnog preseka širine b i visine h je

Ako se ovde z’ izrazi pomoću w’’, dobija se

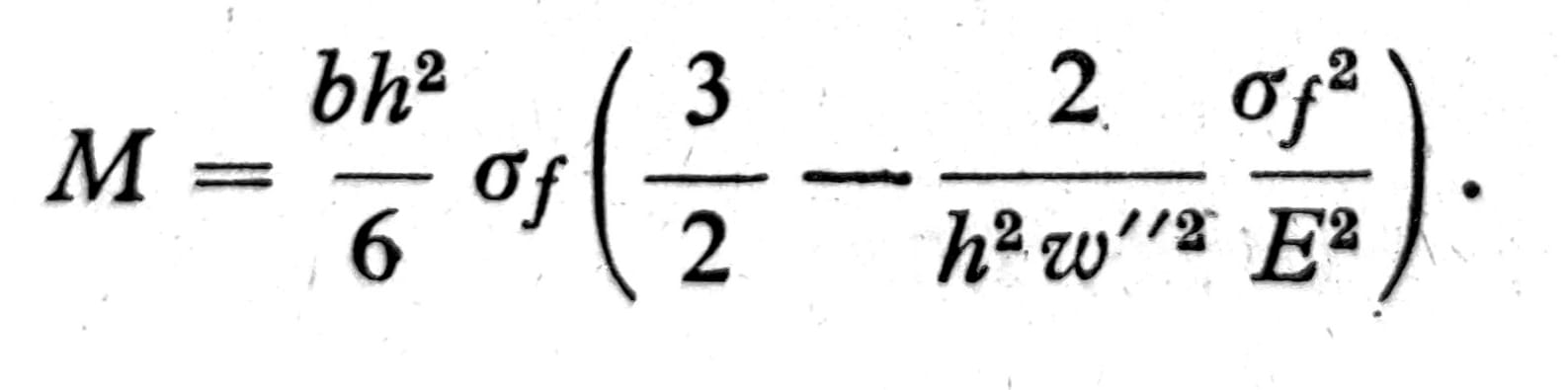
Kod I-preseka i njima sličnih, tok M-w’’ krive u plastičnoj oblasti još više je položen i moment pri kome nastupa tečenje je tada praktično jednak najvećem momentu savijanja koji presek uopšte može da podnese. Zbog toga se značaj plastičnog savijanja u građevinarstvu ne sastoji u povećanju momenta savijanja koji presek može da nosi, nego u tome što velika lokalna deformacija koja nastupa na granici tečenja može da dovede do povoljne promene rasporeda sila kod statički neodređenih sistema.

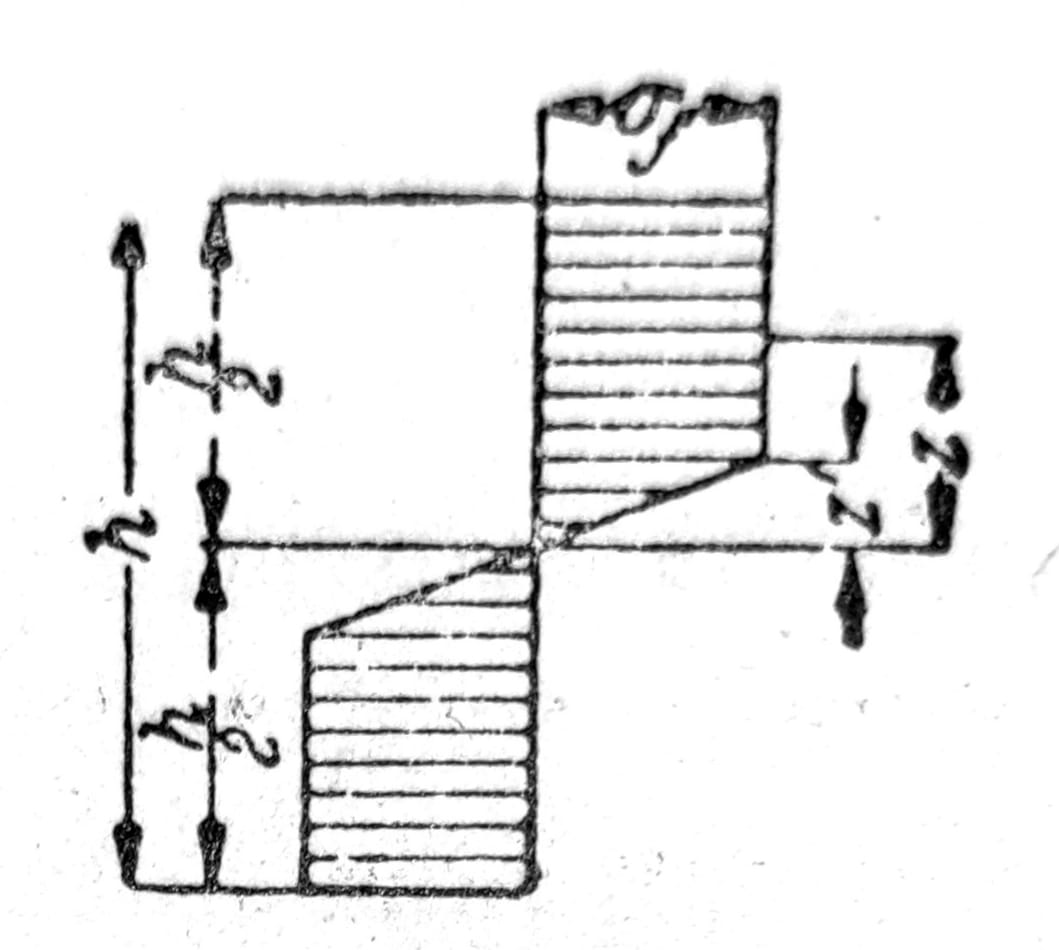
Sl. 9

Ovo se može objasniti na primeru kontinualnog nosača preko dva polja. Neka nosač (sl. 10) ima polja jednake dužine, konstantan presek i neka je opterećen jednakopodeljenim opterećenjem. Tada je pre dostizanja granice tečenja moment nad osloncem M_B = pl²/8. Ako se opterećenje p toliko poveća da moment u oslonačkom preseku dostigne vrednost M_f pri kojoj nastupa tečenje, pri daljem povećanju opterećenja na tome mestu će se povećati i krivina bez osetnog priraštaja momenta. Stvara se tzv. plastični zglob, tj. nosač se pod dopunskim opterećenjem ponaša tako kao da nad srednjim osloncem postoji zglob. Opterećenje se može dalje povećavati sve dok i na mestu najvećeg momenta u polju ne počne tečenje. Dalje povećanje momenta savijanja nije više moguće i nosivost nosača je iscrpljena. Teret pod kojim nastupa ovo stanje naziva se granično opterećenje.

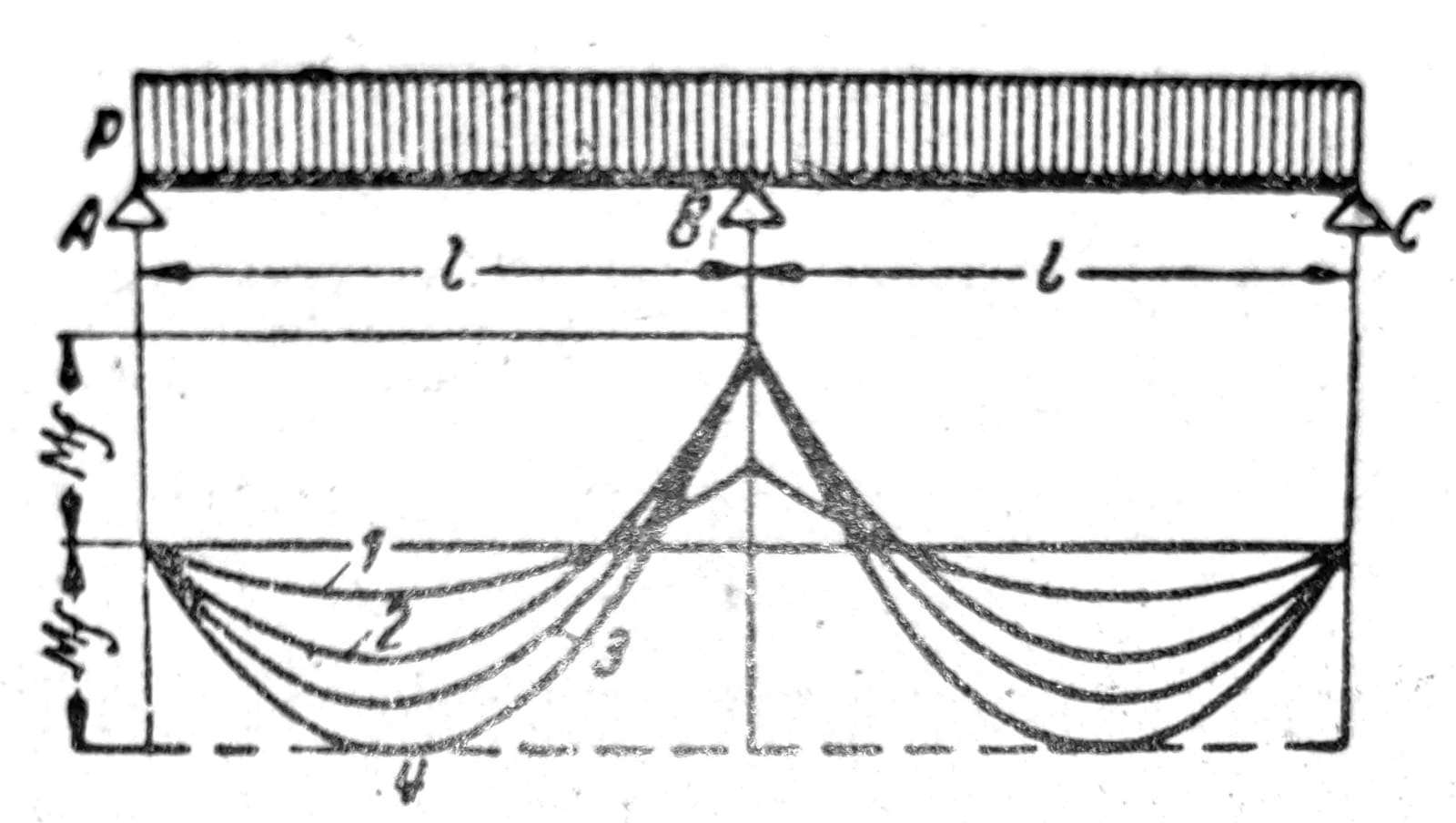
Sl. 10

Uopšte se može očekivati da će u jednom n puta statički neodređenom sistemu morati da se pojavi (n+1) plastičnih zglobova pre nego što sistem postane pomerljim i time dostigne svoju granicu nosivosti. Ovo pravilo, međutim, ima izuzetaka u oba pravca. Kao što navedeni primer pokazuje, na granici nosivosti mogu da se pojave istovremeno dva nova plastična zgloba (u oba polja), tako da dotle još nepomerljiv sistem odjedanput prelazi u sistem sa dva stepena slobode. S druge strane moguće je da i sa manje od (n+1) plastičnih zglobova nosivost bude lokalno iscrpljena, npr. kada kod kontinualnog nosača popusti samo jedno polje. Sl. 11 pokazuje kako se to može dogoditi kod jednog statički dvostruko neodređenog sistema sa n=2 plastična zgloba. Ako se na desnoj strani nosača doda još i četvrto polje, nosač postaje trostruko statički neodređen, pa je dovoljno (n-1) plastičnih zglobova da se samo levo polje dovede do granice nosivosti.

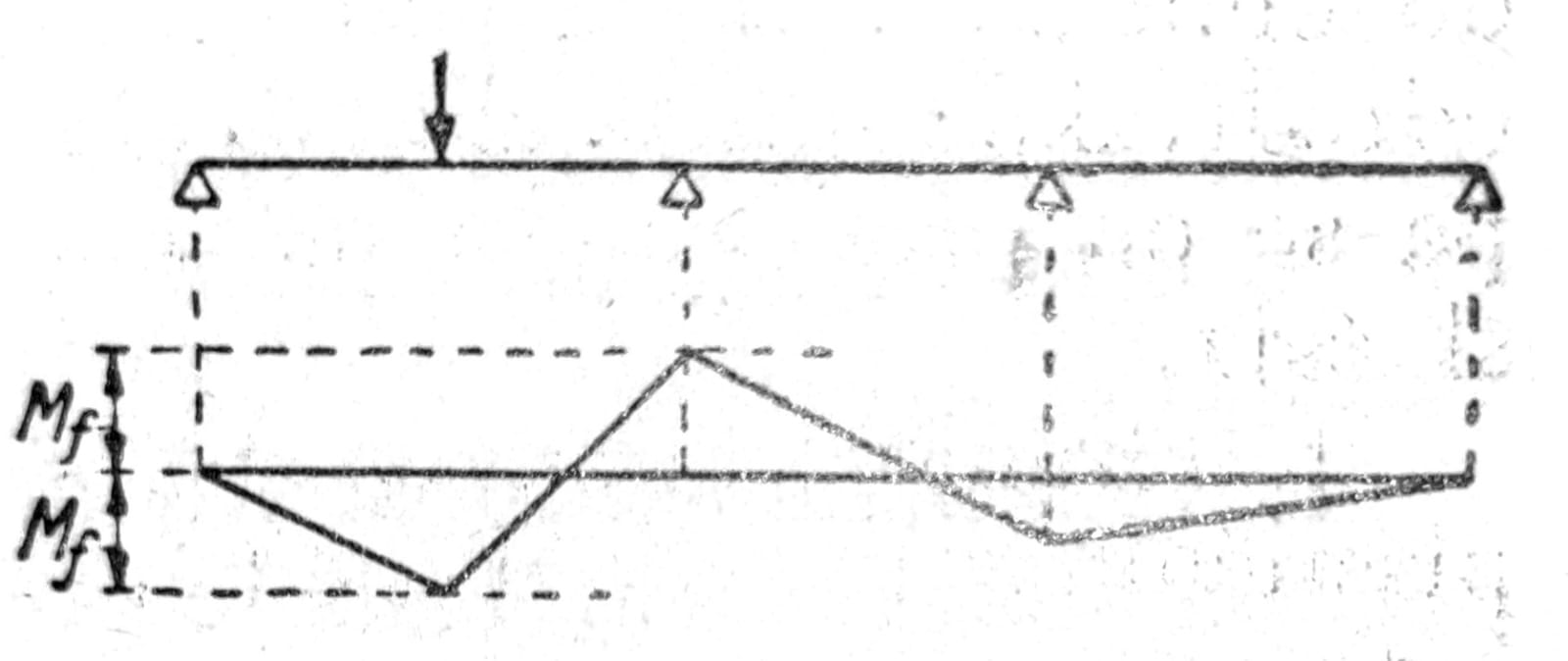
Sl. 11

 

Smičući naponi pri savijanju

Elementarni proračun

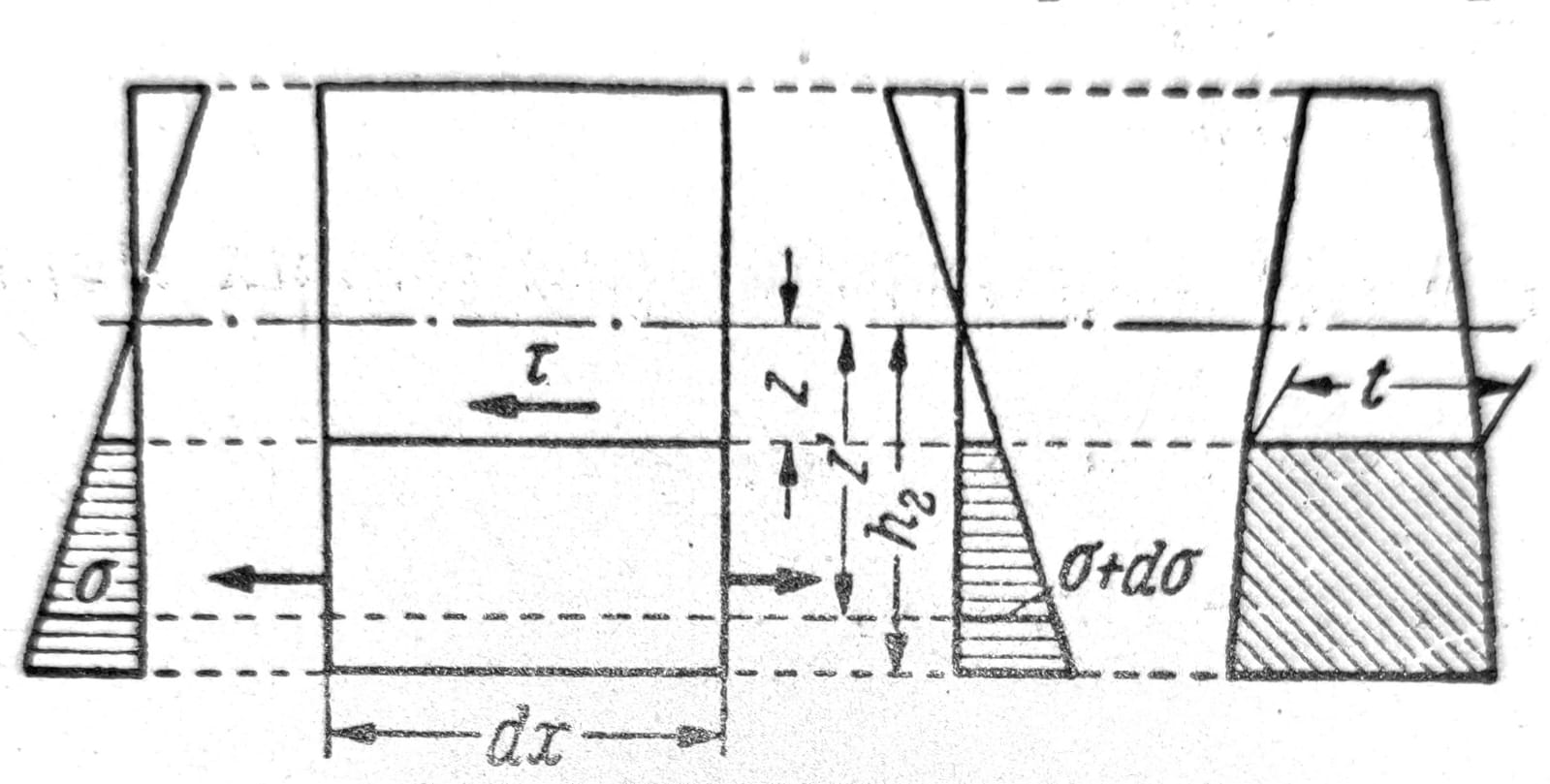
Sl. 12

Normalni naponi σ, tj. naponi koji se ustvari pojavljuju usled savijanja nisu jedini naponi u savijenom štapu, nego se pored njih pojavljuju i smičući naponi usled dejstva trasverzalne sile. S obzirom na to da je osnovna karakteristika tehničke teorije savijanja u tome što se zanemaruju deformacije usled smičućih napona, ovi se mogu odrediti samo iz uslova ravnoteže. Da bi se ovaj postavio, element grede dx seče se, kao što je na sl. 12 naznačeno, horizontalnom ravni na dva dela, pa se postavlja uslov ravnoteže horizontalnih sila koje napadaju na donji deo. Na levoj strani to su unnutrašnje sile izražene naponima σ usled savijanja, kome treba integrirati od z’ = z do z’ = h₂

Na desnoj strani deluju isti naponi, ali povećani za diferencijal u skladu sa odgovarajućim momentom savijanja M + dM. Razlika između sila na obe strane elementa mora da bude u ravnoteži sa silom usled smičućih napona τ koji deluju u horizontalnoj presečnoj površini t dx:

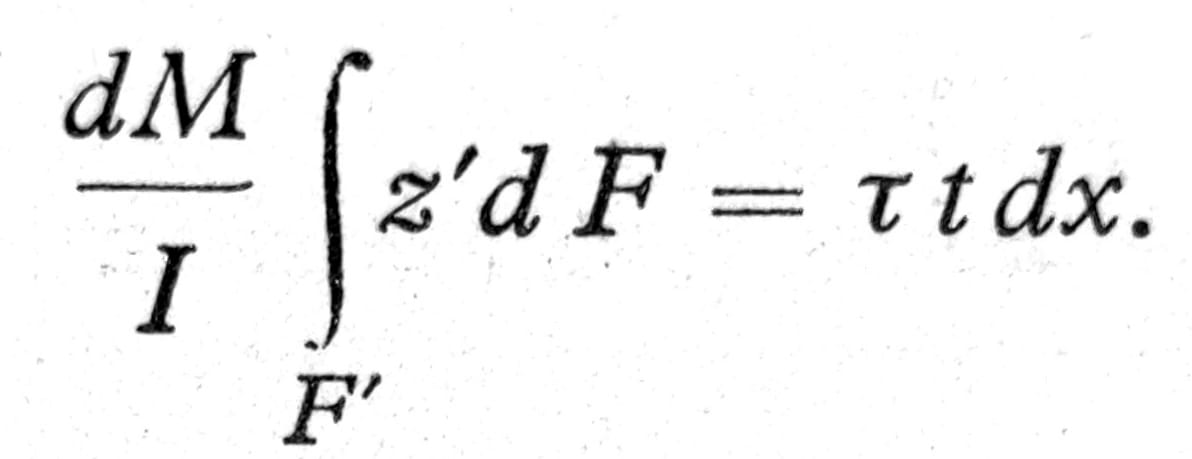
Ovde integral predstavlja statički moment dela poprečnog preseka izdvojenog horizontalnom poprečnom ravni u odnosu na težišnu osovinu preseka. On se označava sa S. Sa dM/dx = Q iz uslova ravnoteže dobija se:

τ = QS/It.  (8)

To je prema stavu o konjugovanosti smičućih napona istovremeno veličina vertikalnog smičućeg napona koji deluje u površini poprečnog preseka i koji je, zajedno sa S i t, funkcija od z.

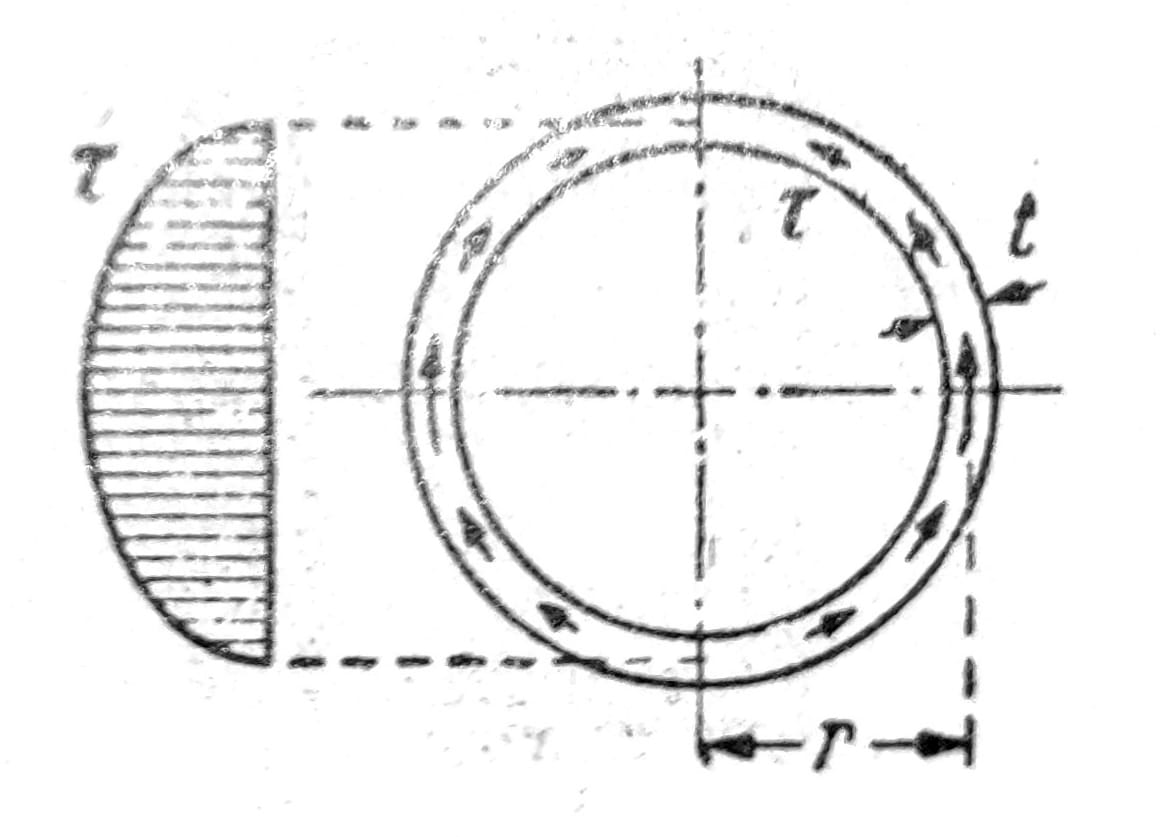
Sl. 13

Sl. 13.1

Jednačina (8) pruža pouzdane podatke kod svih preseka sa tankim zidovima ako se presečna ravan ne postavi paralelno sa neutralnom osovinom, nego u pravcu debljine zida. Prema tome I-profil seče se poprečno preko rebra i poprečno preko flanše, čime se dobija raspored napona prikazan na sl. 13.1. Kod prstenastog preseka (sl. 13) smičući naponi su raspoređeni simetrično u odnosu na vertikalni prečnik i levo i desno na neutralnoj liniji dostižu maksimum

τ = Q / πrt.

Ako je presek razrezan na najvišem ili najnižem mestu, raspored smičućih napona se ne menja; međutim, ako je razrezan na desnom kraju horizontalnog prečnika (sl. 14), smičući napon na tom mestu jednak je nuli, dok mu se vrednost udvostručava na levom kraju istoga prečnika.

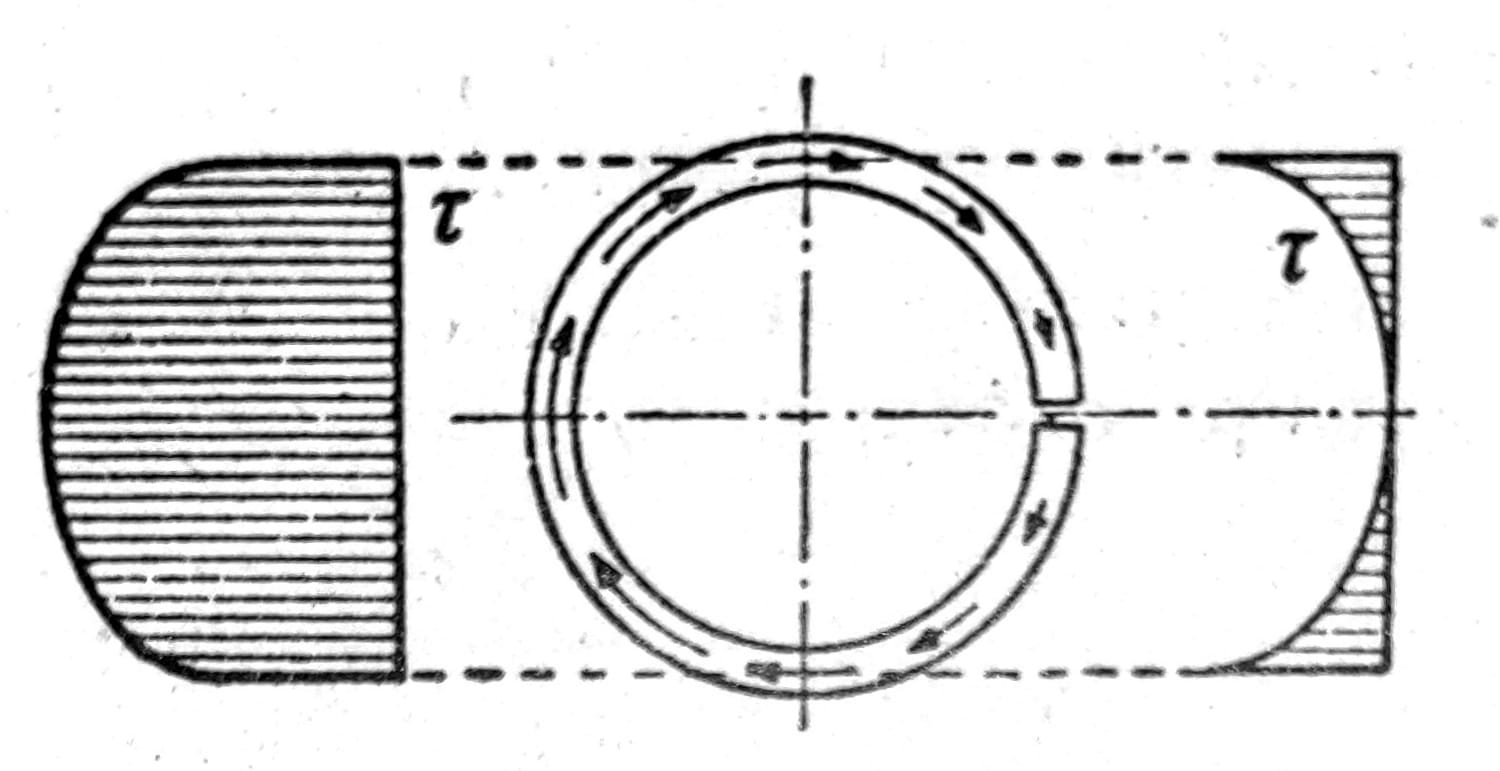
Sl. 14

Puni preseci

Kod punih preseka proizvoljnog oblika problem smičućih napona je usko povezan sa problematikom torzije. Elementarna jednačina (8) u tom slučaju više nije pouzdana. Za kružni presek poluprečnika r jednačina (8) daje

τ = 4Q / 3πr²

kao srednju vrednost smičućeg napona duž neutralne osovine, a tačna vrednost je samo za nekoliko procenata veća.

Središte smicanja

Ako se za U-presek proračunaju smičući naponi na način opisan iznad, dobija se raspored napona prikazan na sl. 15. Rezultanta odgovarajućih unutrašnjih sila je transverzalna sila Q. Iz slike se može videti njen položaj u odnosu na presek, dakle da ona niti prolazi kroz težište preseka, niti leži u ravni rebra. Ako transverzalna sila sračunata na osnovu spoljnih sila nema položaj prikazan na sl. 15, nosač nije opterećen samo na savijanje, već i na torziju.

Ako se za isti poprečni presek odredi rezultanta koja odgovara smičućim naponima za neko horizontalno opterećenje, dobija se napadna linija horizontalne transverzalne sile. U preseku ovih dveju napadnih linija nalazi se karakteristična tačka za dati poprečni presek, koja se naziva središte smicanja M. U nosaču se ne pojavljuju naponi usled torzije kada središta smicanja svih poprečnih preseka leže na jednoj pravoj, a svi tereti upravni na osovinu štapa prolaze kroz tu pravu. U protivnom moment svakog tereta u odnosu na pravu koja spaja središta smicanja i predstavlja torziono smicanje.

Sl. 15

Uticaj transverzalne sile na savijanje

Tehnička teorija savijanja zasniva se na zanemarivanju deformacija usled smičućih napona. Prema tome ona se stvarno može primeniti na vitke štapove, kod kojih je ovo zanemarenje opravdano i gde transverzalna sila nema osetan uticaj na savijanje.

Iskustvo je međutim pokazalo da se tehnička teorija savijanja može sa izvesnim uspehom primeti i na kratke, visoke nosače, za koje ona u stvari uopšte nije namenjena. Tada se ukazuje potreba da se uticaj deformacije usled smičućih napona, koji je u ovoj teoriji zanemaren, uzme, bar približno, naknadno u obzir.

Isto tako kao i smičući naponi τ usled transverzalnih sila i odgovarajuća klizanja γ’ = τ/G raspoređena su neravnomerno po preseku. Zbog toga se uvodi njihova srednja vrednost γ, koja se određuje tako da transverzalna sila pri ovoj srednjoj vrednosti deformacije vrši na elementu grede dx deformacioni rad jednak onome koji bi se dovio integriranjem radova smičućih napona na pojedinim zapreminskim elementima koji sačinjavaju uočeni element grede:

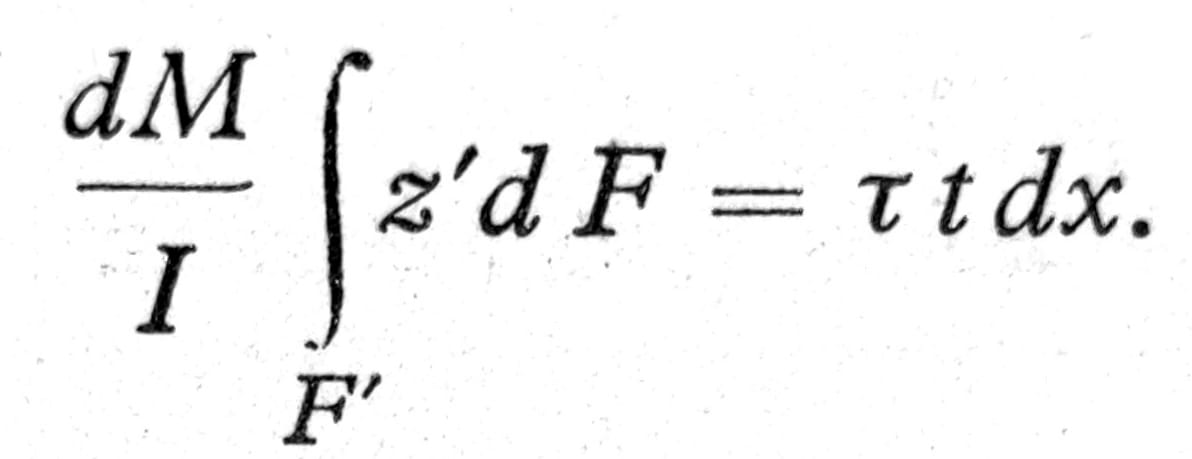
odakle je

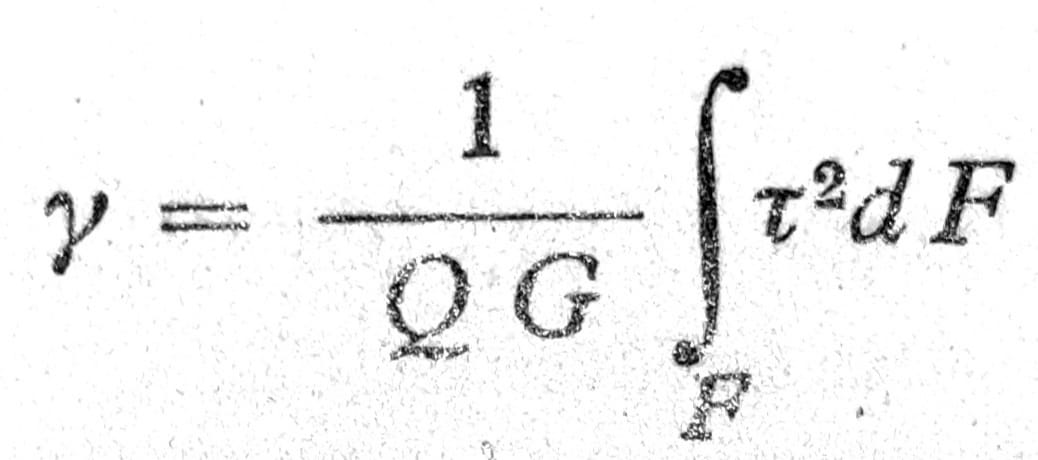
Integral se može proračunati kada je poznat raspored smičućih napona po preseku. Pošto su svi smičući naponi proporcionalni sa Q/F, to je njegova vrednost proporcionalna sa Q₂/F² * F, pa stavljajući da je ona κQ²/F, dobija se

γ = κQ / GF.

Konstanta κ naziva se koef. rasporeda smičućih napona. Za pravougaone preseke je κ=1,2.

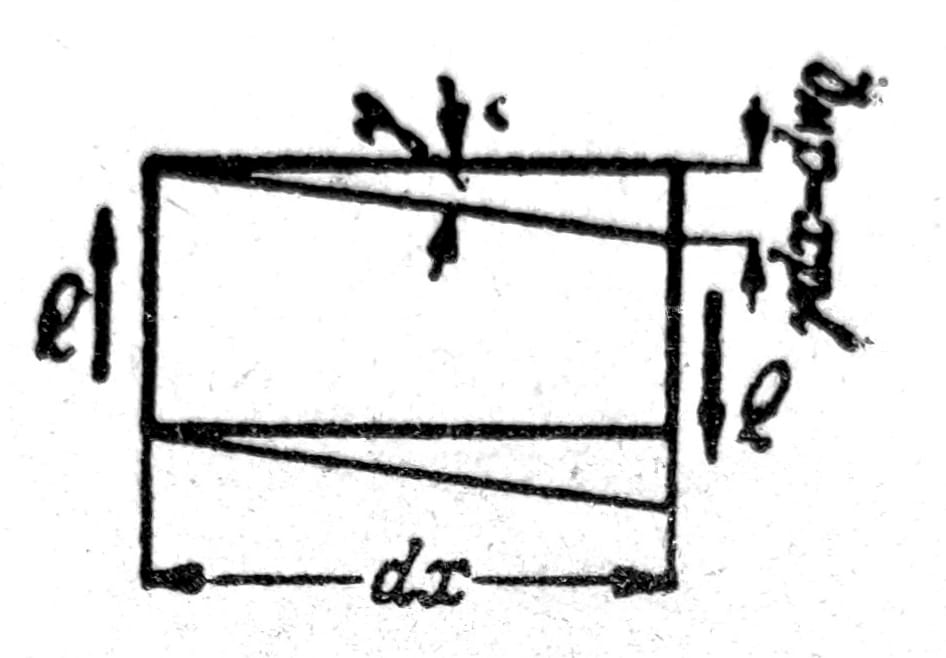
Sl. 16

Kada je poznat koef. κ, a time i srednje klizanje γ, može se sračunati dopunski ugib w_Q, nastao dejstvom transverzalnih sila, koji treba dodati ugibima w: jer prema sl. 16 je

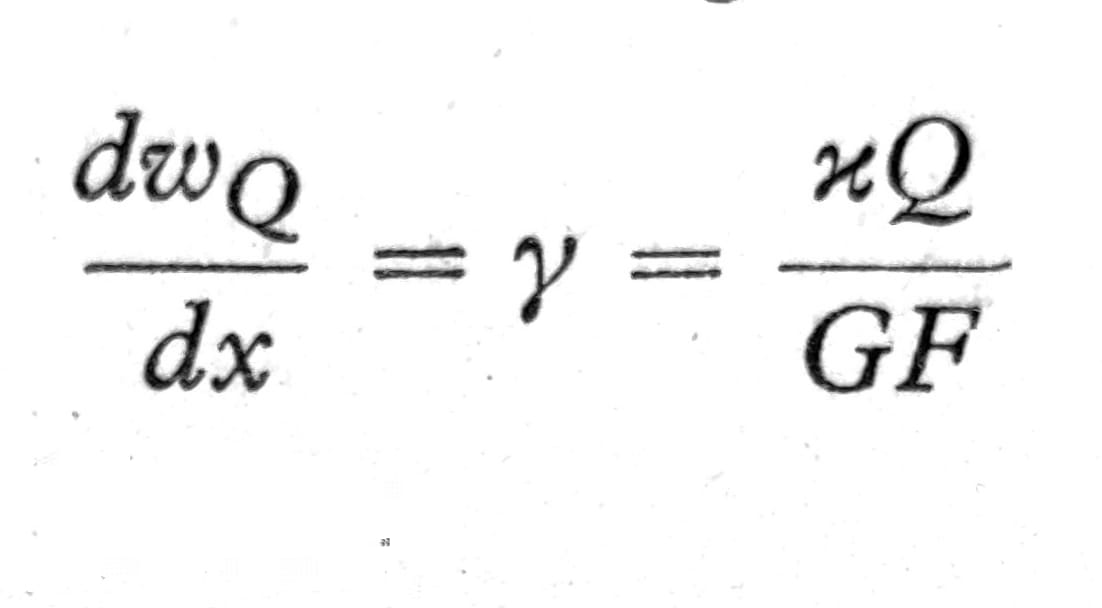
pa je zbog Q = dM/dx:

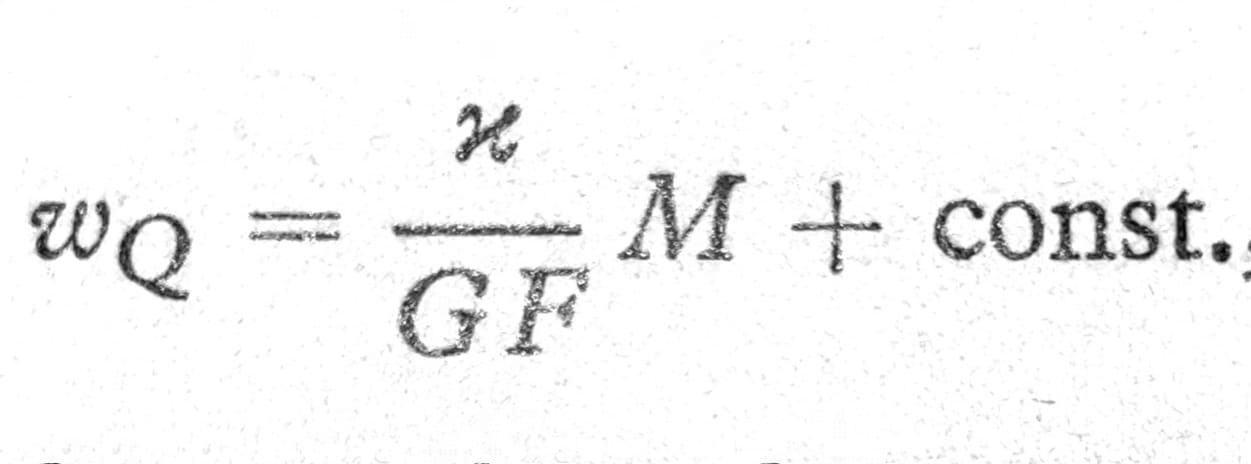
pri čemu se integraciona konstanta dobija iz jednog graničnog uslova.