Teorija elastičnosti - Ljuske

Ljuskama se nazivaju površinski nosači, čija srednja površina nije ravna nego je primetno ispupčena. Njihovo statičko ponašanje znatno odstupa od ponašanja ploče. Kada imaju pogodan oblik, njihovo je naprezanje znatno manje, njihova krutost u odgovarajućoj meri veća, a proračun u većini slučajeva prostiji.

Naprezanje svake ljuske može se razložiti na dva dela: membransko naprezanje i savijanje. Membranski naponi se slično kao i naponi kod ploče opterećene u svojoj ravni mogu izraziti pomoću presečnih sila u tangencijalnoj ravni – to su npr. u preseku x=const. normalna sila N_x=σ_x*t i smičuća sila N_xy=τ_xy*t, gde je t debljina ljuske. Naponi usled savijanja su isti kao i kod ploča i mogu se predstaviti momentima savijanja M_x, torzionim momentima M_xy i smičućim silama Q_x.

Bitne osobine ljuski zasnivaju se na činjenici da po pravilu naponi usled savijanja nemaju ni veličinu ni značaj membranskih napona, tako da se često mogu potpuno zanemariti. U tom slučaju su svi naponi ravnomerno podeljeni po debljini ljuske i deluju tangencijalno na srednju površinu. Proračuni koji se zasnivaju na ovim pretpostavkama ulaze u okvir membranske teorije ljuski.

 

Membranska teorija rotaciono simetričnih ljuski pod rotaciono simetričnim opterećenjem

Opšti obrasci

Za koordinatne linije usvajaju se meridijani i paralelni krugovi u srednjoj površini ljuske, pa su koordinate: azimut ϑ (“geografska dužina”) i nagib φ tangente na meridijan prema ravni upravnoj na osovinu simetrije (sl. 1a). Prema tome su presečne sile: normalna sila N_φ u pravcu meridijana i normalna sila N_ϑ u prstenu (sl. 1b). Smičuće sile N_φϑ ne pojavljuju se kod rotaciono simetričnog naprezanja. Opterećenje na jedinicu površine označava se na sledeći način (sl. 1b): Y tangencijalno na meridijan, pozitivno u pravcu u kome φ raste, Z normalno na ljusku, pozitivno ka osovini simetrije.

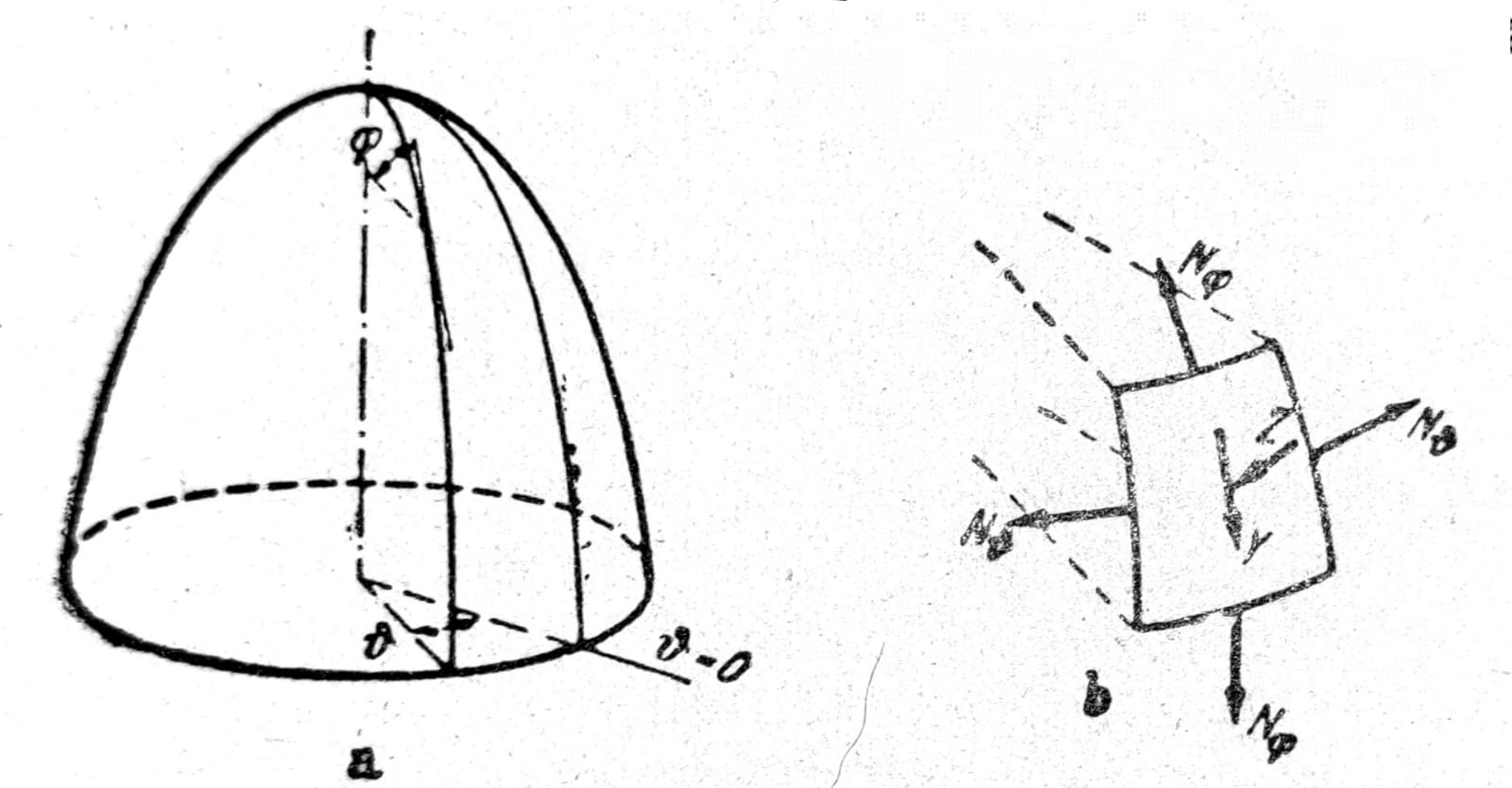
Sl. 1

Sl. 2

Neka je poluprečnik krivine meridijana r₁. On je funkcija ugla φ pa je jednačinom r₁=r₁(φ) određen oblik meridijana. Ova se može smatrati za jednačinu meridijana i glasi, npr.

za krug                                       r₁=a=const.

za parabolu                                  r₁=a/cos³φ

za elipsu          r₁=a²b²(a²sin²φ+b²cos²φ)^-3/2

Za sračunavanje normalne sile N_φ u pravcu meridijana treba postaviti uslov ravnoteže dela ljuske koja leži iznad paralelnog kruga φ (sl. 2). Rezultanta R tereta Y i Z koji napadaju ovaj deo je vertikalna, s obzirom na simetriju. Njena veličina se dobija integriranjem po površini ljuske od φ’=0 do φ’=φ. Površina elementa ljuske je dF=r₁dφ’*rdϑ, pa je vertikalna komponenta opterećenja (Ysinφ’+Zcosφ’)dF. Za ceo prstenast deo ljuske koji leži između krugova φ’ i φ’+dφ’ rezultanta spoljnog opterećenja je:

dR=2πr (Ysinφ’+Zcosφ’) r₁dφ’,

odakle se integriranjem po φ’ za deo ljuske koji leži iznad paralelnog kruga φ’=φ dobija:

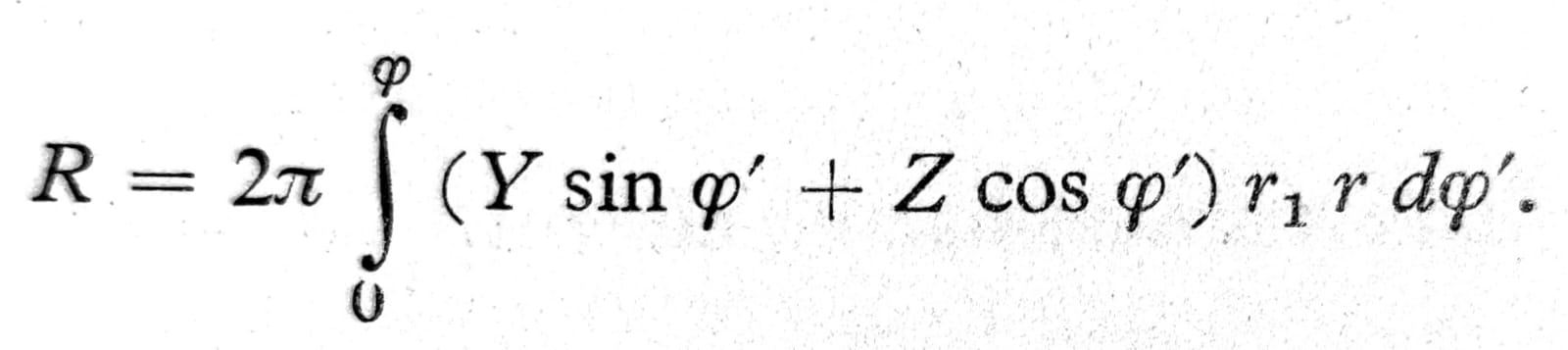
Jedn. 1

Ovo opterećenje primaju normalne sile u pravcu meridijana, koje deluju po obimu uočenog kruga; vertikalna komponenta rezultante ovih sila je 2πr * N_φ sinφ, pa se izjednačavanjem odavde dobija tražena normalna sila

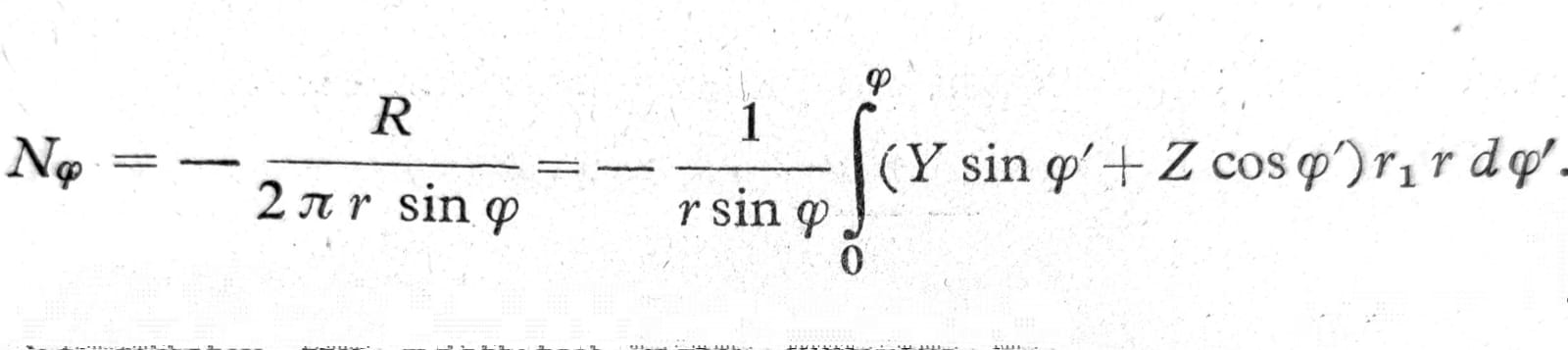
Jedn. 2

Ako je ljuska na gornjem delu isečena duž kruga φ=φ₀ (npr. otvor za osvetljenje u kupoli), donja granica integrala je, razume se, φ₀, a ne nula. Ako na ivici ljuske koja je nastala na ovaj način deluje i opterećenje R₀, to i njega treba dodati rezultanti R (sl. 3).

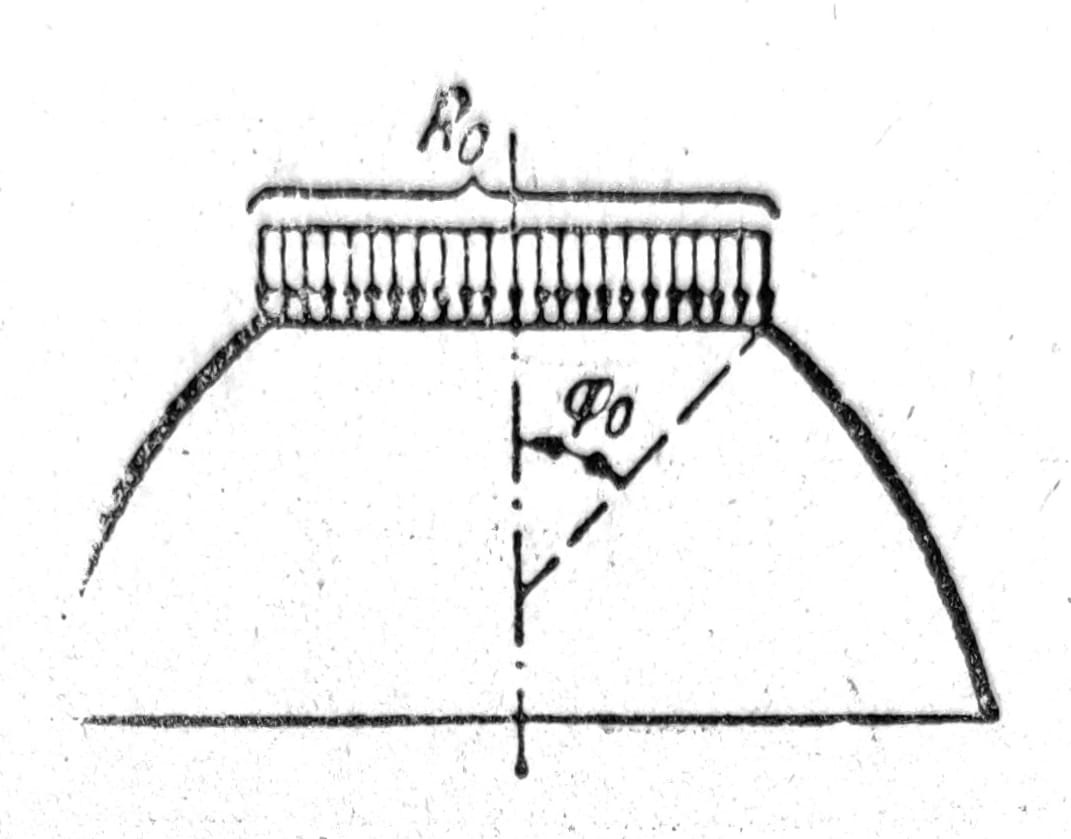
Sl. 3

Za određivanje normalne sile N_ϑ treba postaviti uslov ravnoteže elementa ljuske upravno na tangencijalnu ravan (sl. 4). Rezultanta spoljnog opterećenja u ovom pravcu iznosi Z r₁ dφ r dϑ. Sile N_φ*r dϑ koje leže u meridijalnoj ravni zaklapaju međusobno mali ugao dφ, pa je njihova rezultanta u pravcu normale na ljusku N_φ r dϑ*dφ. Slično tome i sile N_ϑ r₁ dφ koje leže u ravni horizontalnog kruga i među sobom obrazuju ugao dϑ imaju rezultantu N_ϑ r₁ dφ*dϑ koja takođe leži u ravni horizontalnog kruga i prema tome sa normalom na ljusku zaklapa ugao 0,5π-φ, tako da u uslov ravnoteže ulazi samo njihova komponenta N_ϑ r₁ dφ dϑ*sinφ. Uslov ravnoteže prema tome glasi

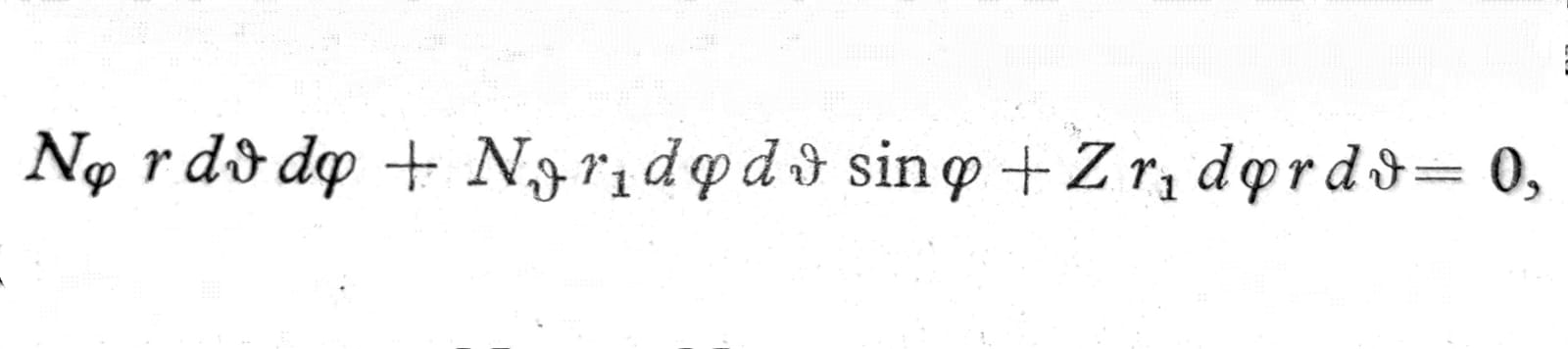
ili, kada se podeli sa r r₁ dϑ dφ:

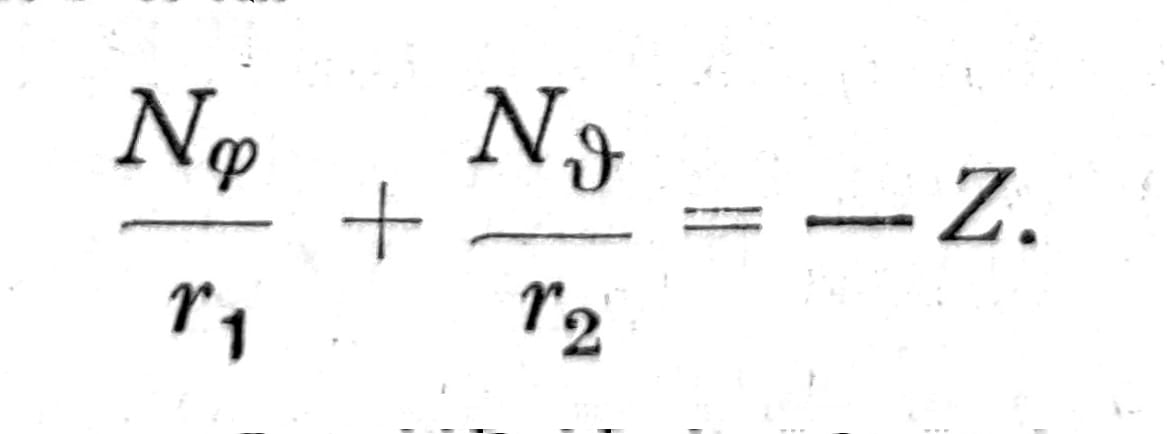
Jedn. 3

Ovde je sa r₂=r/sinφ označen drugi glavni poluprečnik krivine ljuske.

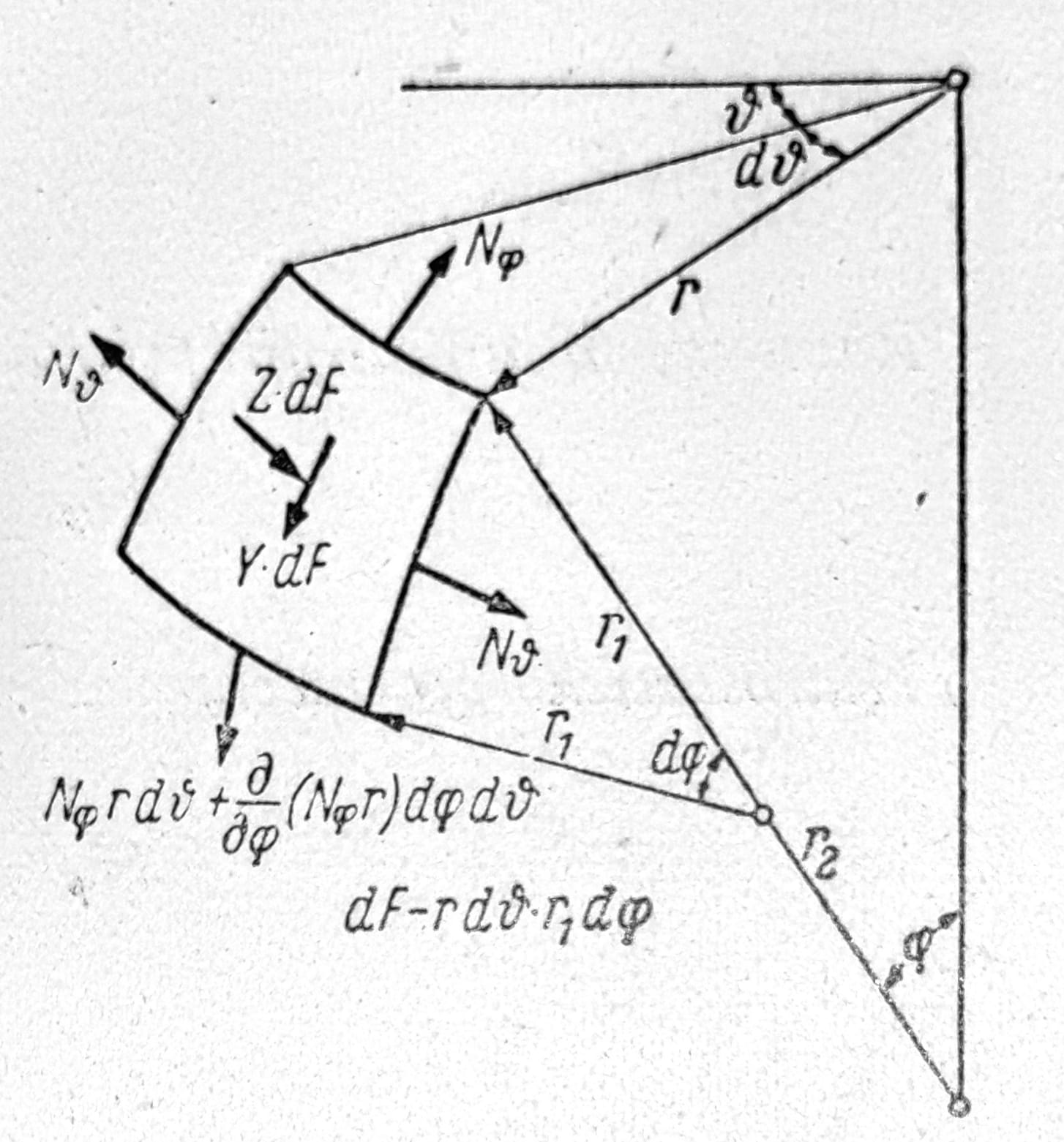
Sl. 4

Kružna kupola

Kada je oblik meridijana analitički dat jednačinom r₁=r₁(φ) i kada su za terete Y(φ) i Z(φ) dati analitički izrazi, presečne sile u ljusci mogu se uvek odrediti integriranjem u zatvorenom obliku ili numerički, koristeći Simpson-ovo pravilo. Za kružnu kupolu prečnika a u sledećem se daju presečne sile za neke slučajeve opterečenja:

Poslednji obrazac, koji za φ=0 daje beskonačne velike presečne sile, važi tek na izvesnom odstojanju od napadne tačke sile. U neposrednoj okolini mesta na kome deluje sila, čak i kada je ona raspodeljena po površini kruga konačnog ali malog prečnika, opterećenje se uglavnom prenosi savijanjem.

Obrasci za ljuske otvorene na gornjem delu mogu se izvesti iz prethodnih, ako se na stvarnom opterećenju doda fiktivni teret P u temenu čija se veličina tako određuje ako ukupna normalna sila u pravcu meridijana koja deluje na gornjoj ivici ljuske φ=φ₀ iznosi N_φ=0, ili je jednaka nekoj vrednosti određenoj spoljnim silama koje ljuska ovde prima.

Konusna ljuska

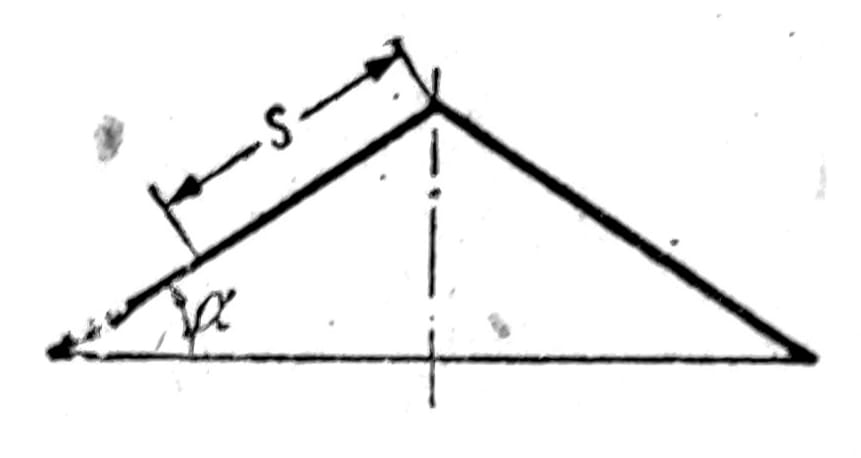
Sl. 5

Kod konusne ljuske se nagib meridijana φ ne može koristiti kao koordinata, jer on ima u svim tačkama istu vrednost. Umesto njega uvodi se odstojanje s od vrha kupole mereno duž izvodnice (sl. 5). Normalna sila u pravcu meridijana u skladu sa tim označava se sa N_s. Potrevni obrasci mogu se dobiti iz navedenih pod 1 kada se izvrši granični prelaz. Iz jednačine (2) dobija se na taj način

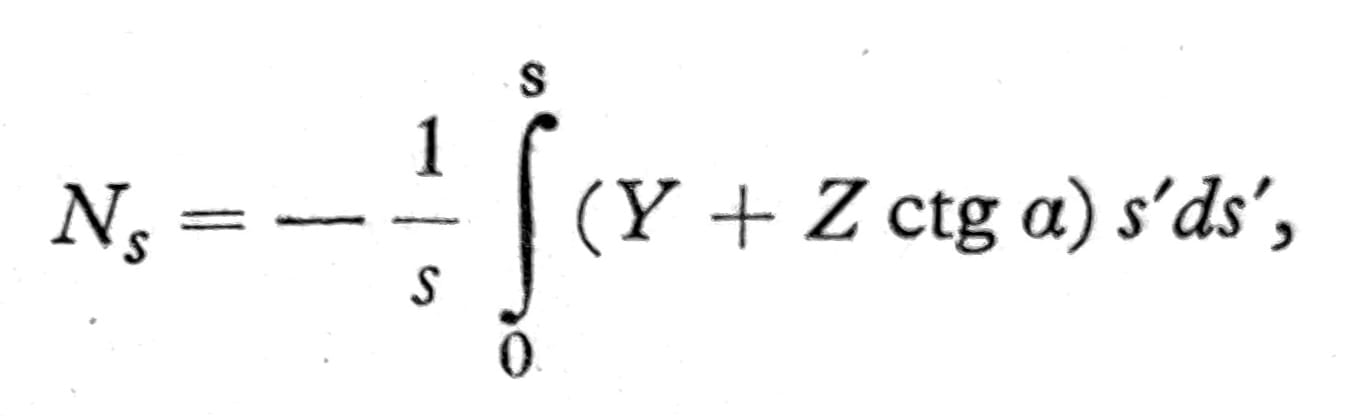
a iz jednačine (3)

N_ϑ = -r₂ Z = -Z s ctga.

Za najvažnije slučajeve opterećenja važe sledeći obrasci:

Grafički postupak za proizvoljni oblik meridijana

Sl. 6

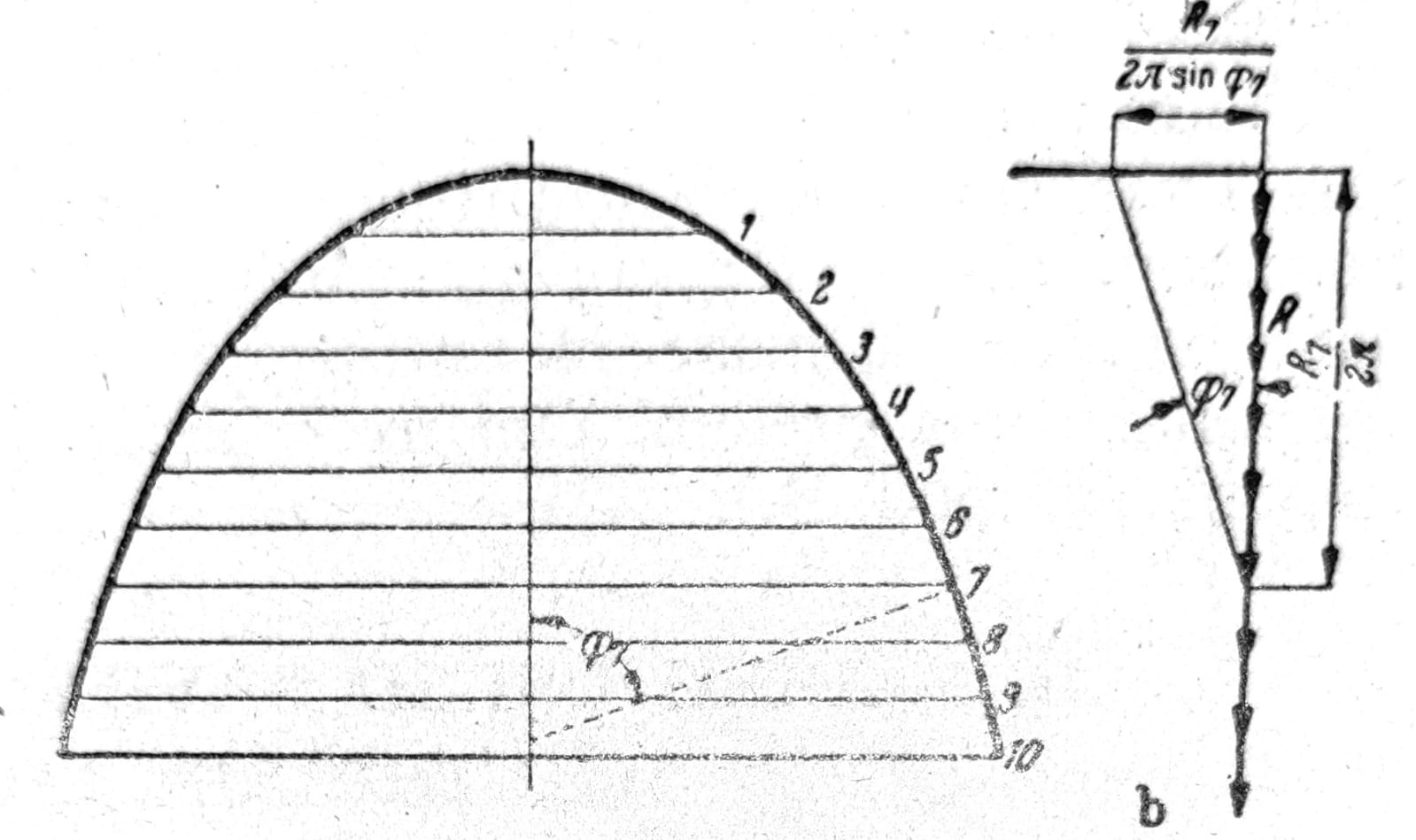
Kad kriva meridijana nije data analitičkim izrazom, nego, recimo, grafički, određivanje poluprečnika krivine je suviše teško i suviše netačno. U tom slučaju pogodnije je koristiti se grafičkim postupkom (sl. 6).

Ljuska se izdeli većim brojem ravni φ=const., sračunaju se težine ΔR prstenastih zona koje leže između ravni i najbolje odmah podeliti sa 2π. Ove sile ΔR/2π nanose se u plan sila (sl. 6b). Ako se zatim, npr., kroz podeonu tačku 7 povuče prava paralelna tangenti na meridijan u tački meridijana 7, horizontala kroz gornju tačku plana sila seći će na njoj duž R₁/2π sinφ₇ iz koje se na osnovu jednačine (2) deljenjem sa odgovarajućim r dobija odgovarajuća normalna sila u pravcu meridijana.

Za određivanje sila u prstenovima služi uslov ravnoteže horizontalnih sila na jednom elementu ljuske. Ako deluju samo vertikalni tereti, ovaj uslov glasi (sl. 4):

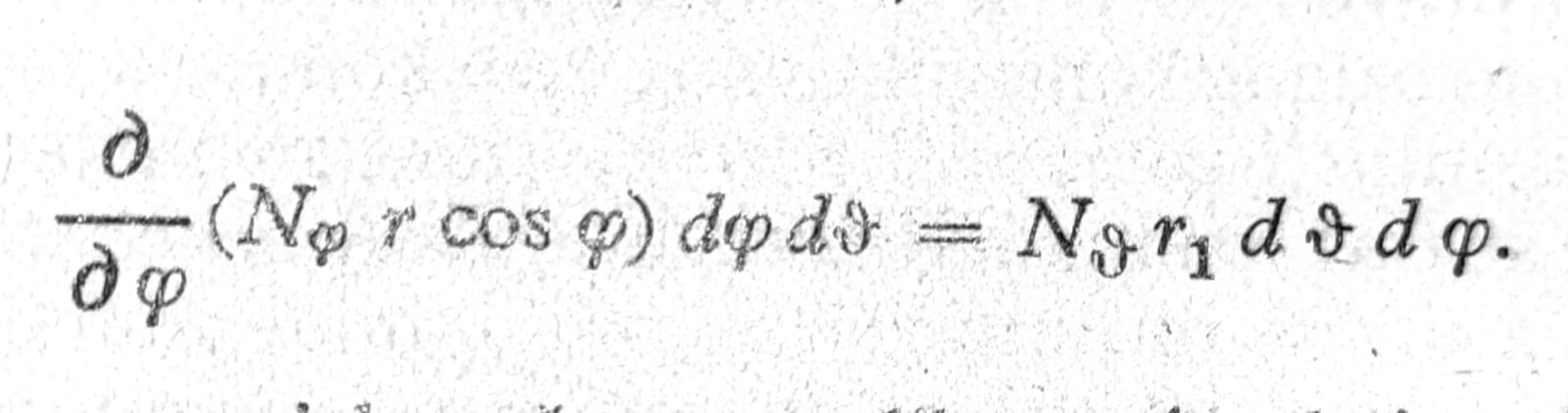
Kada se ovde dφ zameni konačnom razlikom Δφ, koja odgovara usvojenoj podeli ljuske i kad se umesto r₁ dφ unese dužina Δs elementa meridijana, odavde se dobija

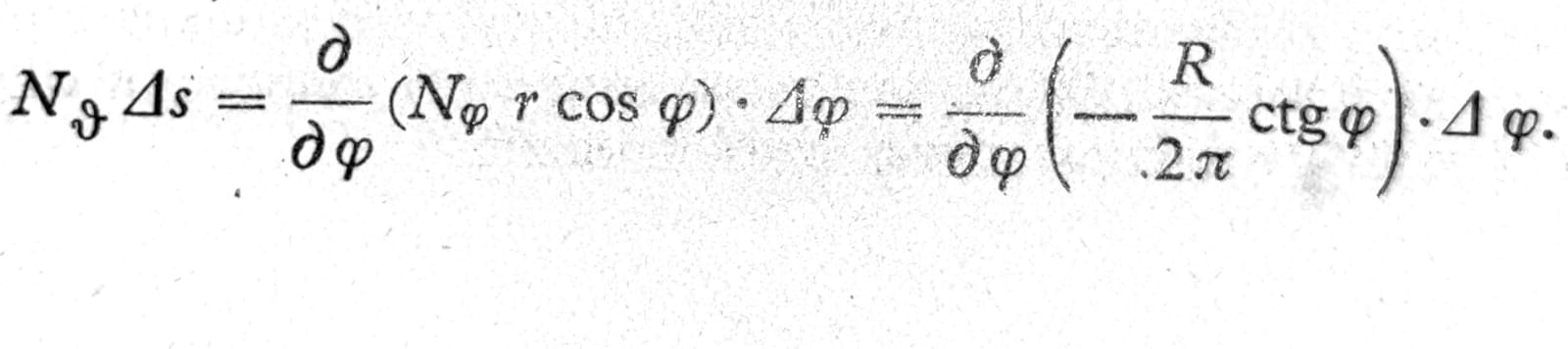
U zagradi na desnoj strani stoji odsečal na horizontalnoj pravoj u planu sila. Celokupna desna strana prema tome predstavlja odsečke između podeonih tačaka na ovoj pravoj. Da bismo ih mogli dovoljno tačno očitati, plan sila treba da bude nacrtan brižljivo i u dovoljno velikoj razmeri.

Zategnuti i pritisnuti prstenovi

Svaka rotaciono simetrična ljuska ograničena je sa jednim ili dva horizontalna kruga (sl. 7). Na ovim ivicama ona može principijelno da primi samo takve terete i reakcije oslonaca, koji imaju pravac tangente na meridijan. Ako spoljne sile imaju drugi pravac, kao npr. opterećenje P od gornjeg dela konstrukcije ili reakcija S dna rezervoara prikazanog na sl. 97, ove sile se moraju, kako je to na slici prikazano, razložiti na komponente u pravcu horizontalnoh kruga i tangente na meridijan. Komponenta P/sinφ₀ ili S/sinφ_u jednaka je normalnoj sili u pravcu meridijana N_φ koja na tome mestu deluje, dok je za prijem horizontalne sile Pctgφ₀ ili Sctgφ_u potreban prsten koji prima zatezanje, odn. pritisak i u kome ovo radijalno opterećenje izaziva normalnu silu + P r₀ ctgφ₀, odn. -S r_u ctgφ_u. Ovakvi se prstenovi, osim na ivicama ljuske, moraju postaviti i na svim onim mestima gde kriva meridijana imaju prelom. Oni uvek izazivaju poremećaj membranskog stanja napona.

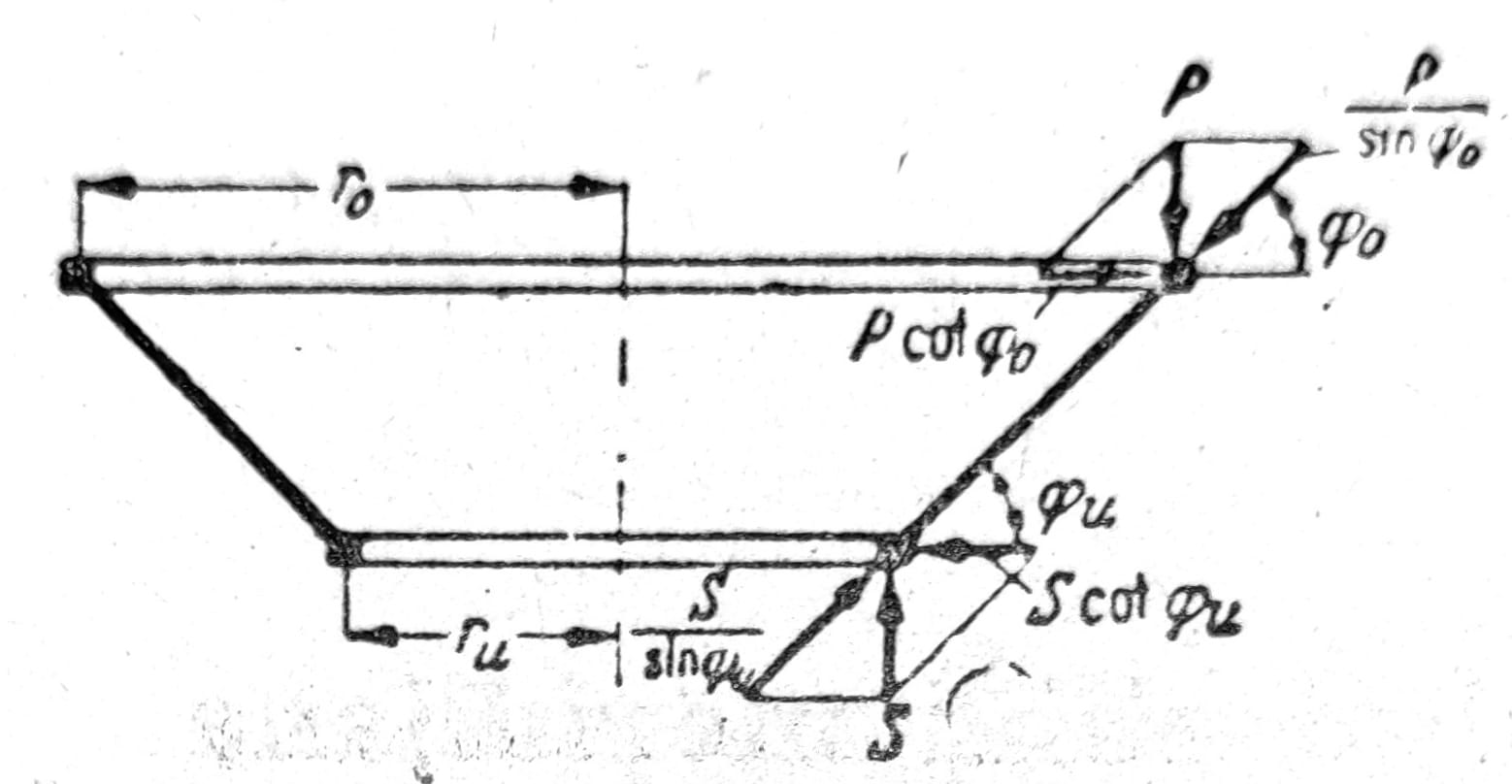
Sl. 7

 

Naponi usled savijanja u rotaciono simetričnim ljuskama

Obrasci membranske teorije ne sadrže dovoljan broj integracionih konstanata da bi se mogli ispuniti svi granični uslovi koji stvarno odgovaraju postavljenom zadatku. Specijalno kod rotaciono simetričnih ljuski, nije moguće nekim pogodnim izborom integracionih konstanata postići da dilatacija ε_ϑ = N_ϑ/Et u pravcu prstena duž ivice ljuske bude jednaka odgovarajućoj dilataciji nekog drugog konstruktivnog dela koji je sa njom na tom mestu čvrsto vezan. Ovo isto važi i za ljuske kod kojih se duž jednog horizontalnog kruga skokovito menja krivina meridijana, debljina ljuske ili opterećenje po jedinici površine. I kada ljuska duž neke ivice nije ukrućena prstenom, ali je na ovome mestu opterećena silama koje imaju komponentu u pravcu normale na ljusku (npr. opterećenje P na sl. 7 kada se zamisli da je prsten uklonjen), ona ne može da primi ovakve terete samo preko membranskih sila. U ovakvim slučajevima smičuća sila i momenti savijanja (sl. 8) igraju bitnu ulogu pri rasporedu sila u ljusci, što se u statičkom proračunu mora uzeti u obzir.

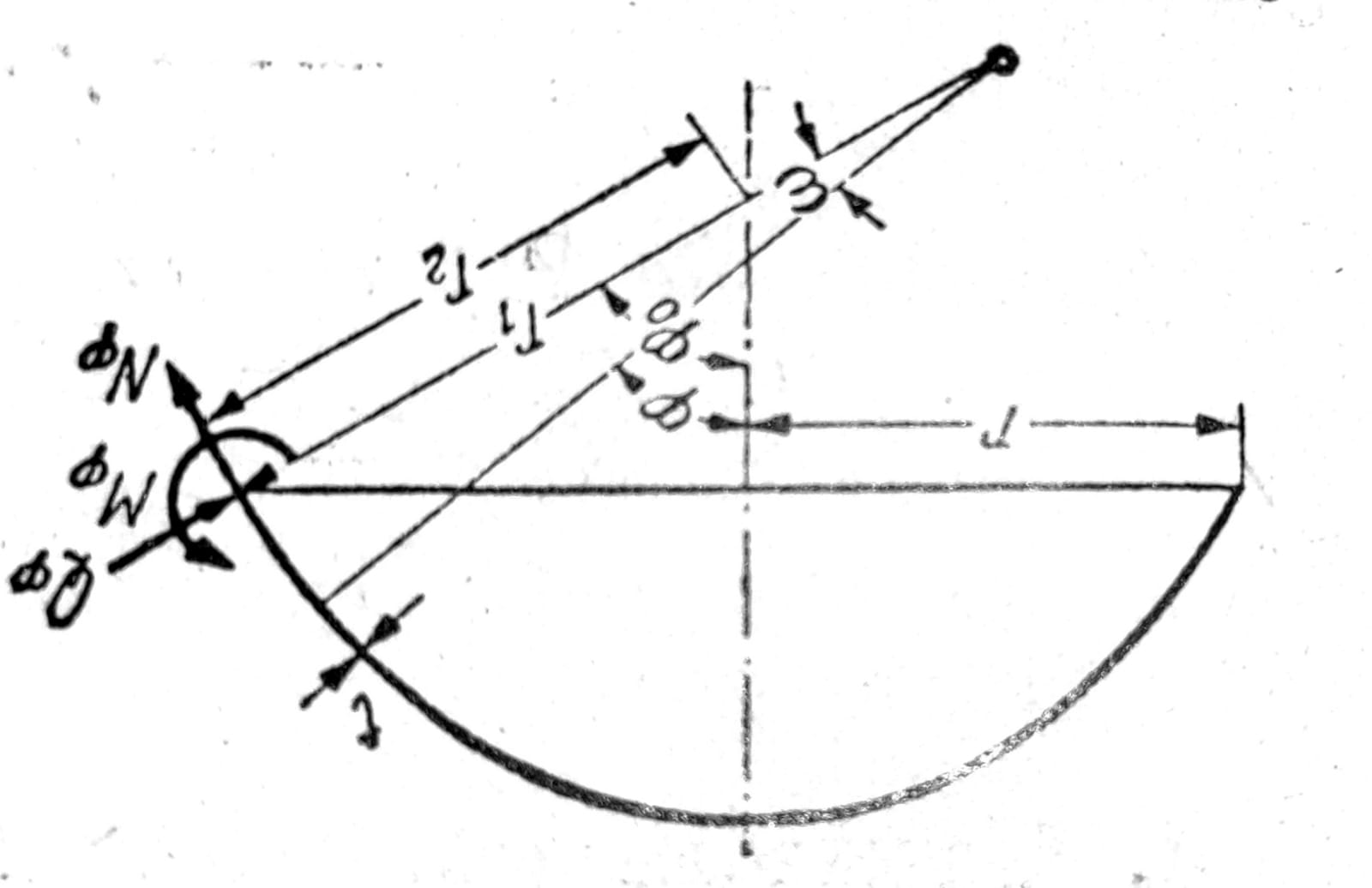
Sl. 8

Tačan proračun ljuske na savijanje, osim u najjednostavnijem specijalnom slučaju cilindrične ljuske, predstavlja veoma težak zadatak. Za ljuske sa tankim zidovima može se izgraditi prosta i vrlo upotrebljiva približna teorija koja se oslanja na činjenicu poznatu iz stroge teorije, da se naponi usled savijanja ograničavaju na relativno usku zonu pored ivice i brzo opadaju sa porastom odstojanja od ivice. Ovo omogućuje da se veliki broj članova u tačnoj diferencijalnoj jednačini zanemari, pa ova dobija uprošćeni oblik.

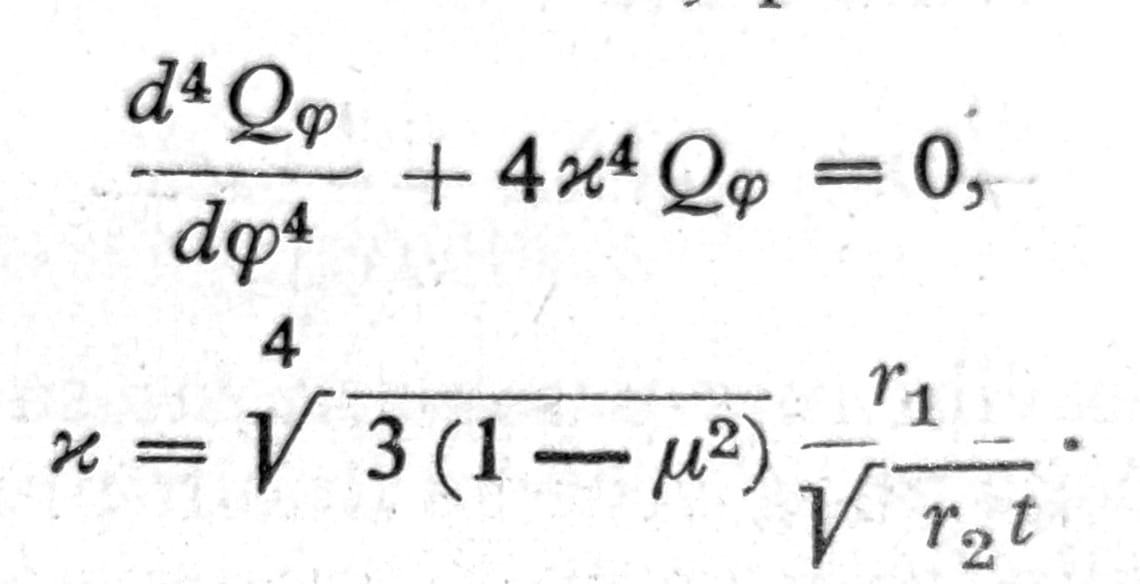
Ako se unutar ivične tone koja je jedino interesantna κ zameni srednjom vrednošću, a ovo je skoro uvek moguće, rešenje jednačine je

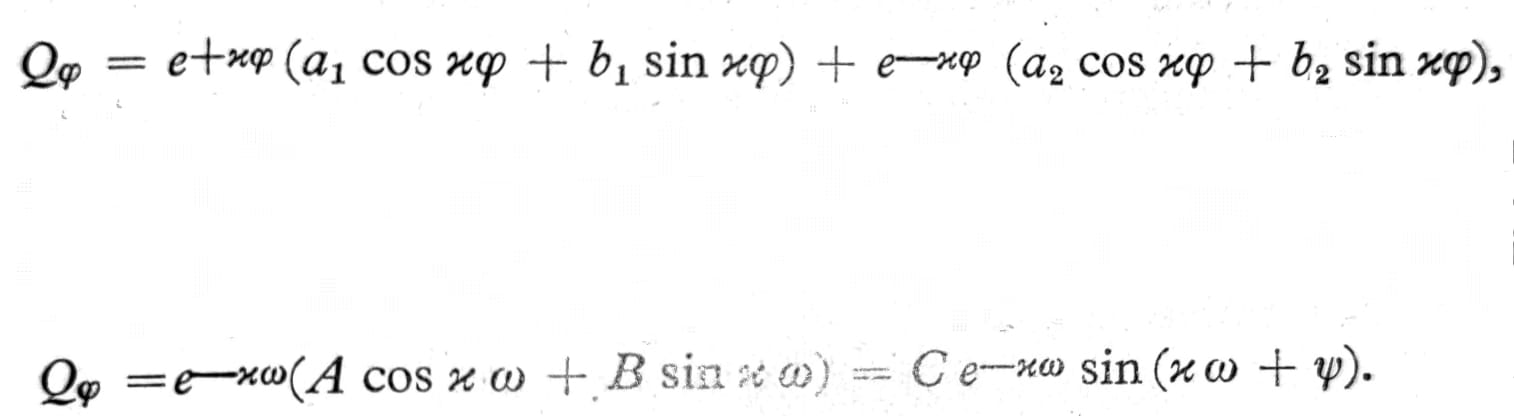
Jedn. 4 i 5

gde su a₁, b₁, a₂, b₂ integracione konstante. Kako je rešenje interesantno samo u blizini ivice φ=φ₀, pogodno je da se ugaono odstojanje ω=φ₀-φ ili ω=φ-φ₀ od ove ivice uvede kao koordinata, pa se transformacijom gore navedenog rešenja dobija drugi navedeni izraz. Ovde se pojavljuju samo dve integracione konstante A, B ili C, ψ, pošto drugi deo rešenja koji sadrži faktor e^κω, i prema tome sa porastom ω ne opada, može da se isključi iz razmatranja.

Na osnovu jednačine 5 dobijaju se sledeće vrednosti za presečne sile i obrtanje κ tangente meridijana:

 

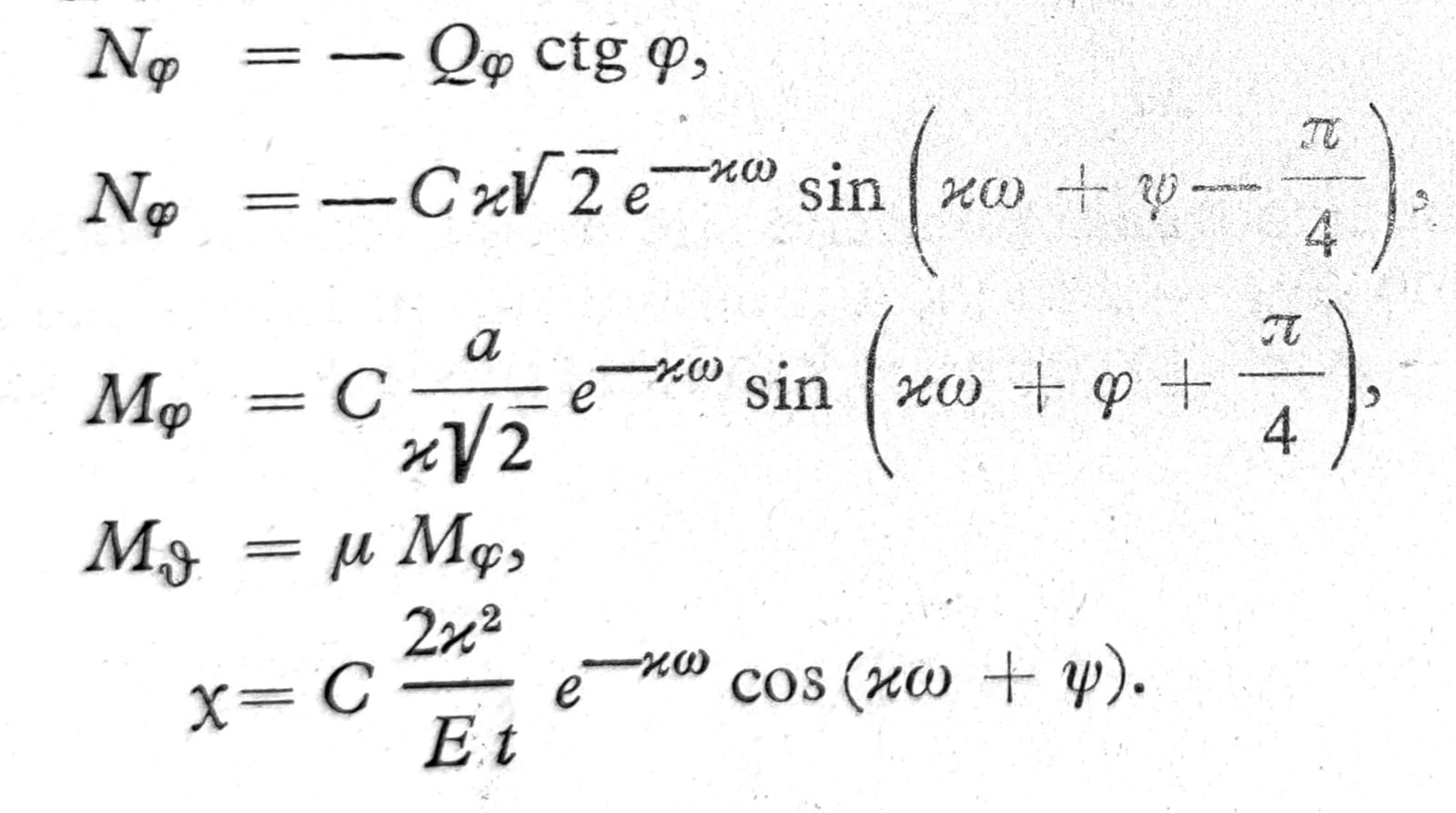
Naponi usled savijanja u rezervoarima oblika kružnog cilindra

Neka je cilindrični rezervoar visine h napunjen vodom (sl. 9), tada je na visini x iznad dva rezervoara pritisak vode p=γ(h-x). Ako se na ovoj visini sa dva horizontalna preseka na odstojanju dx. iseče iz rezervoara prsten i ovaj podeli duž jednog prečnika na dva dela, uslov ravnoteže jednoga od njih daje membransku silu u prstenu N_φ=pa. Ako je debljina  rezervoara na ovome mestu t, dilatacija u prstenu je ε_φ=N_φ/Et i prema tome povećanje poluprečnika rezervoara (ugib) je

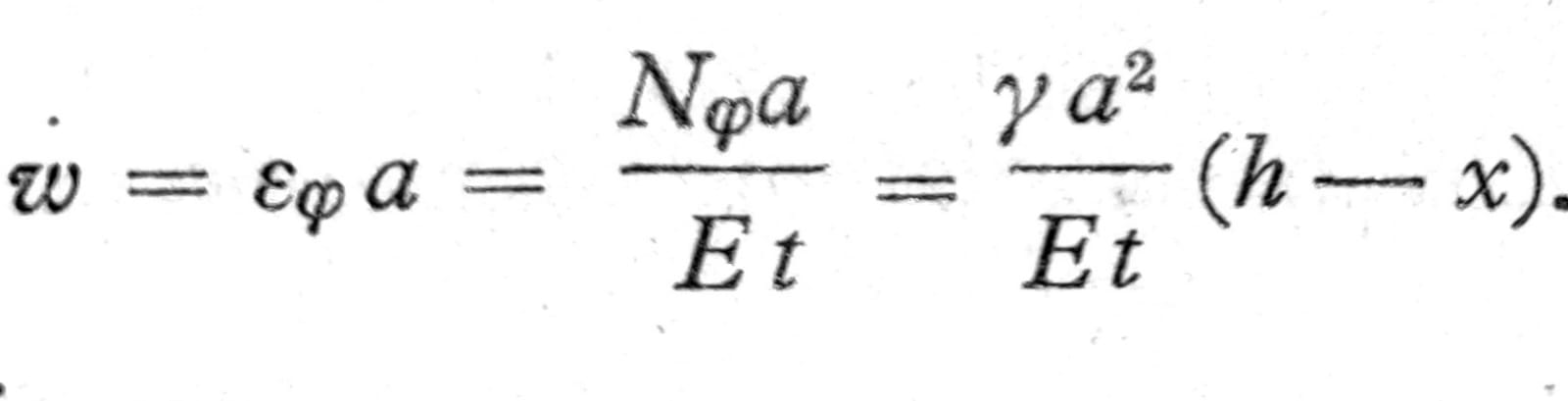
Na donjoj ivici x=0 je prema tome

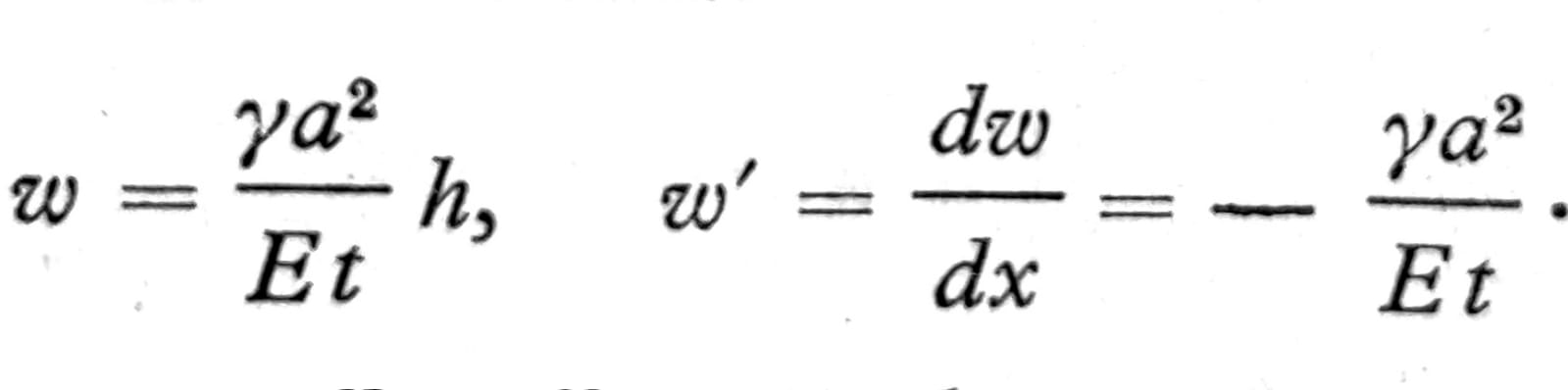
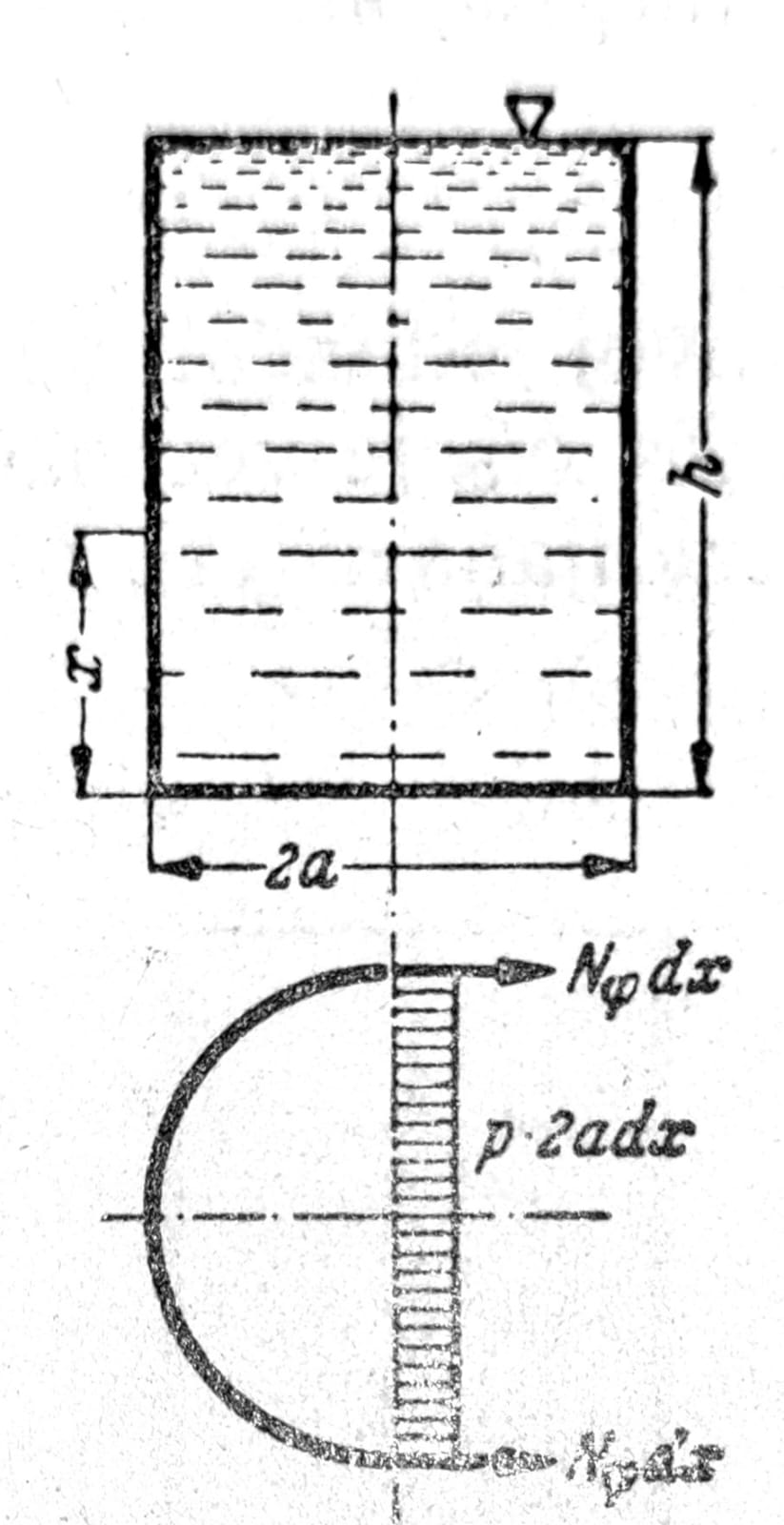
Sl. 9

Ni jedno ni drugo po pravilu nije u saglasnosti sa graničnim uslovima, jer je deformacija zida sprečena zbog veze sa dnom rezervoara. Pri tome se na vezi između dna i zida cilindra pojavljuju transverzalne sile Q_x0 i momenti M_x0 (sl. 11), čiju veličinu treba tako odrediti da zajedno sa upravo sračunatim membranskim silama u ljusci izazivaju ovu deformaciju na ivici ljuske koju dopušta dno.

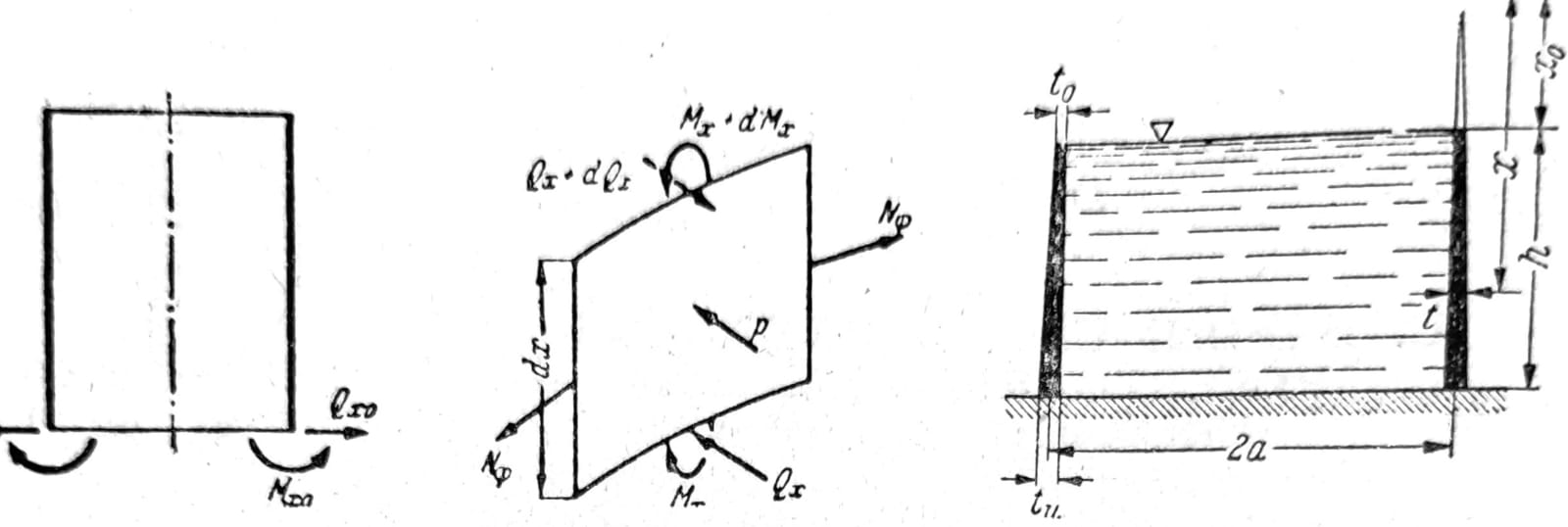
Sl. 10, 11, 12, respektivno

Na sl. 11 prikazan je element ljuske dx*a dφ sa silama koje na njega deluju. Uslov ravnoteže sila u pravcu normale na ljuski daje

dQ_x a dφ + N_φ dx dφ = p a dφ dx,

odakle je deljenjem sa dx dφ:

a Q’_x + N_φ = p a.

Iz uslova da je moment oko horizontalne tangente na cilindar nula dobija se:

dM/dx = M’_x = Q_x

Eliminacijom transverzalne sile Q_x iz ovih dveju jednačina sledi

a M’’_x + N_φ = p a.

Jedn. 6

U ovoj jednačini se ove nepoznate presečne sile mogu izraziti pomoću ugiba w. Za N_φ je već nađeno N_φ=Etw/a, a moment je proporcionalan krivini meridijana w’’, tj. M_x=Kw’’, pri čemu je kao i kod ploča K=Et³/12(1-μ²) krutost ljuske, koja može da bude promenljiva sa x. Ako se ovi izrazi za prosečne sile unesu u jednačinu (6), dobija se diferencijalna jednačina teorije rezervoara:

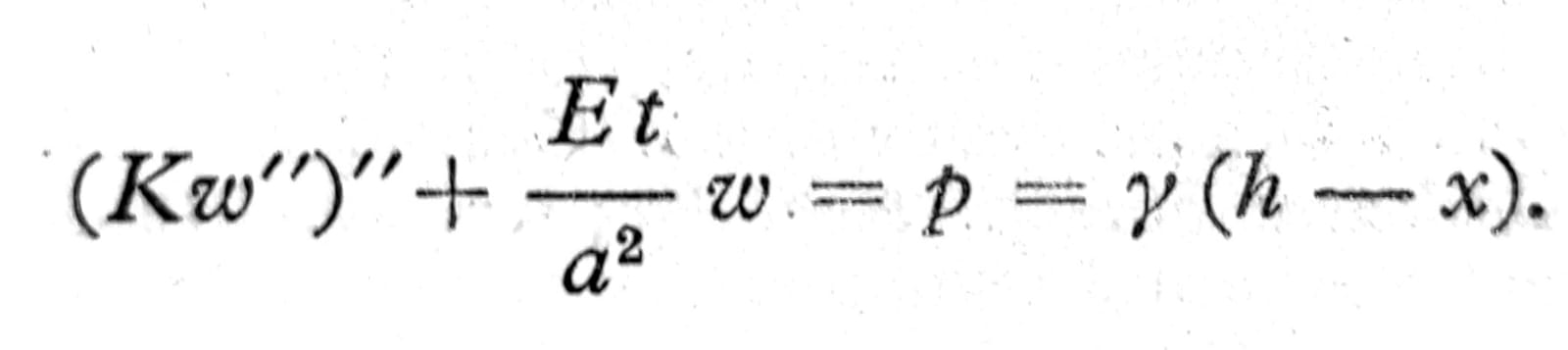
Za rezervoar čija je debljina zida nepromenljiva rešenje glasi:

Jedn. 7

gde je λ⁴=3(1-μ²)/a²t². Ako je λh veliko (recimo, veće od 3), zgodnije je da se umesto hiperboličkih funkcija uvedu eksponencijalne, pa je:

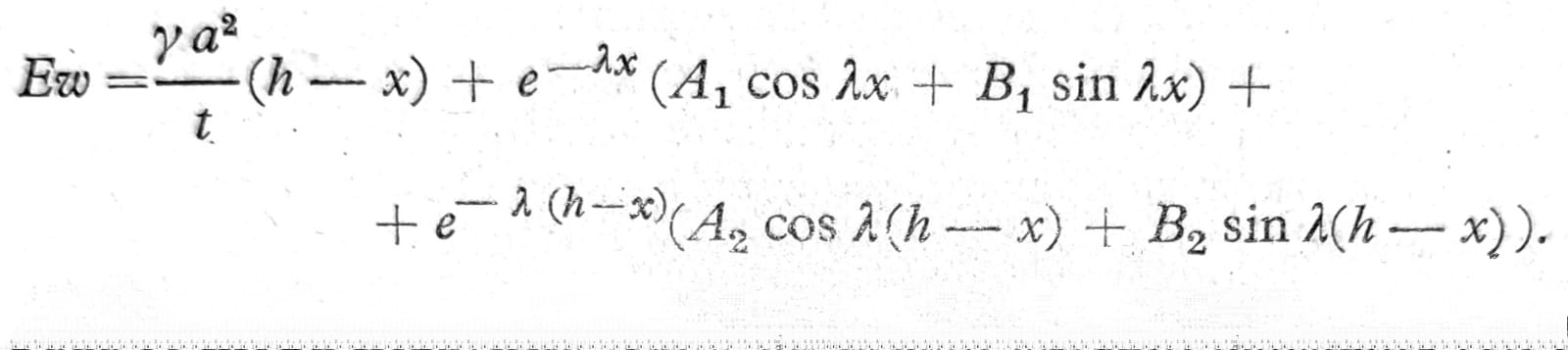
Jedn. 8

Tada se mogu nezavisno jedne od drugih odrediti konstante A₁, B₁ iz graničnih uslova na donjoj, a konstante A₂, B₂ iz graničnih uslova na gornjoj ivici, pri čemu se po pravilu dobija A₂=B₂=0. Na osnovu jednačine (8) i (7) dobijaju se presečne sile, kada se račun sprovede u obrnutom pravcu i svuda uvede jednačina (8) i (7); tako je npr. za A₂=B₂=0:

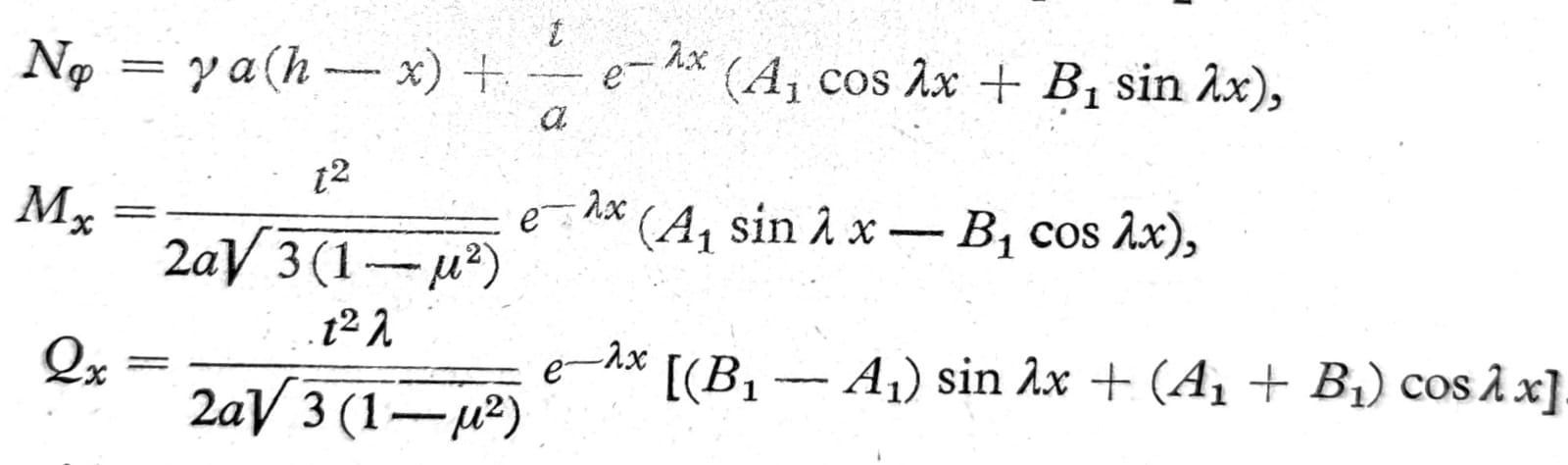
Kada su zidovi rezervoara kruto uklješteni u ploču, na dnu rezervoara koja je dovoljno debela da se može smatrati krutom, konstante A₁, B₁ treba odrediti iz uslova da je x=0, w=0 i w’=0 pa se dobija:

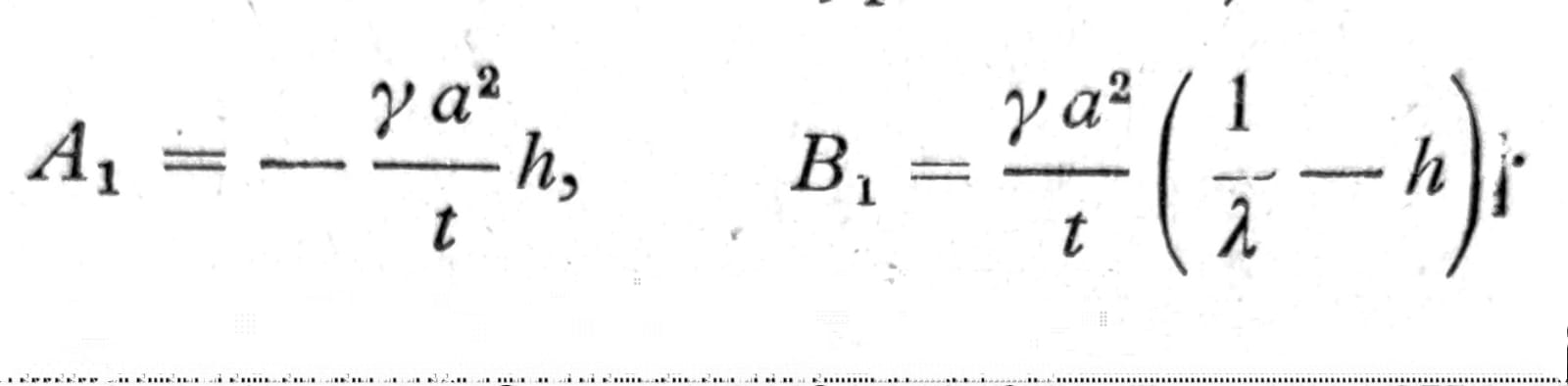
Ako je dno rezervoara elastična ploča ili ljuska, transverzalne sile Q_x i momente M_x duž ivičnog kruga između dna i zida cilindra treba odrediti metodama teorije statički neodređenih sistema na osnovu zahteva da M_x i w’ za oba dela imaju istu vrednost.