Teorija elastičnosti - Ploče

Presečne sile. Diferencijalna jednačina.

Osnovni pojmovi

Pločom se u otpornosti materijala ne naziva naprosto svako telo pločastog oblika, već samo ono:

1. za koje je površina koja na svakom mestu polovi debljinu ploče ravan („srednja ravan“),

2. čija je debljina mala prema dimenzijama ploče u njenoj srednjoj ravni,

3. kod koje opterećenje nema komponentu paralelnu srednjoj ravni.

Ako opterećenje ne ispunjava ovaj uslov, ono se uvek može razložiti na jedan deo koji ga ispunjava i opterećenje koje deluje isključivo u srednjoj ravni.

Za određivanje položaja tačaka ploče koristi se ravan koordinatni sistem x, y u srednjoj ravni i odstojanje z tačke od srednje ravni. Ako se sa t označi debljina ploče, onda je jednačina njenih graničnih površina data sa z=±t/2, pri čemu t može da bude nepromenljivo, ili data funkcija od x, y (ploča promenljive debljine).

Presečne sile

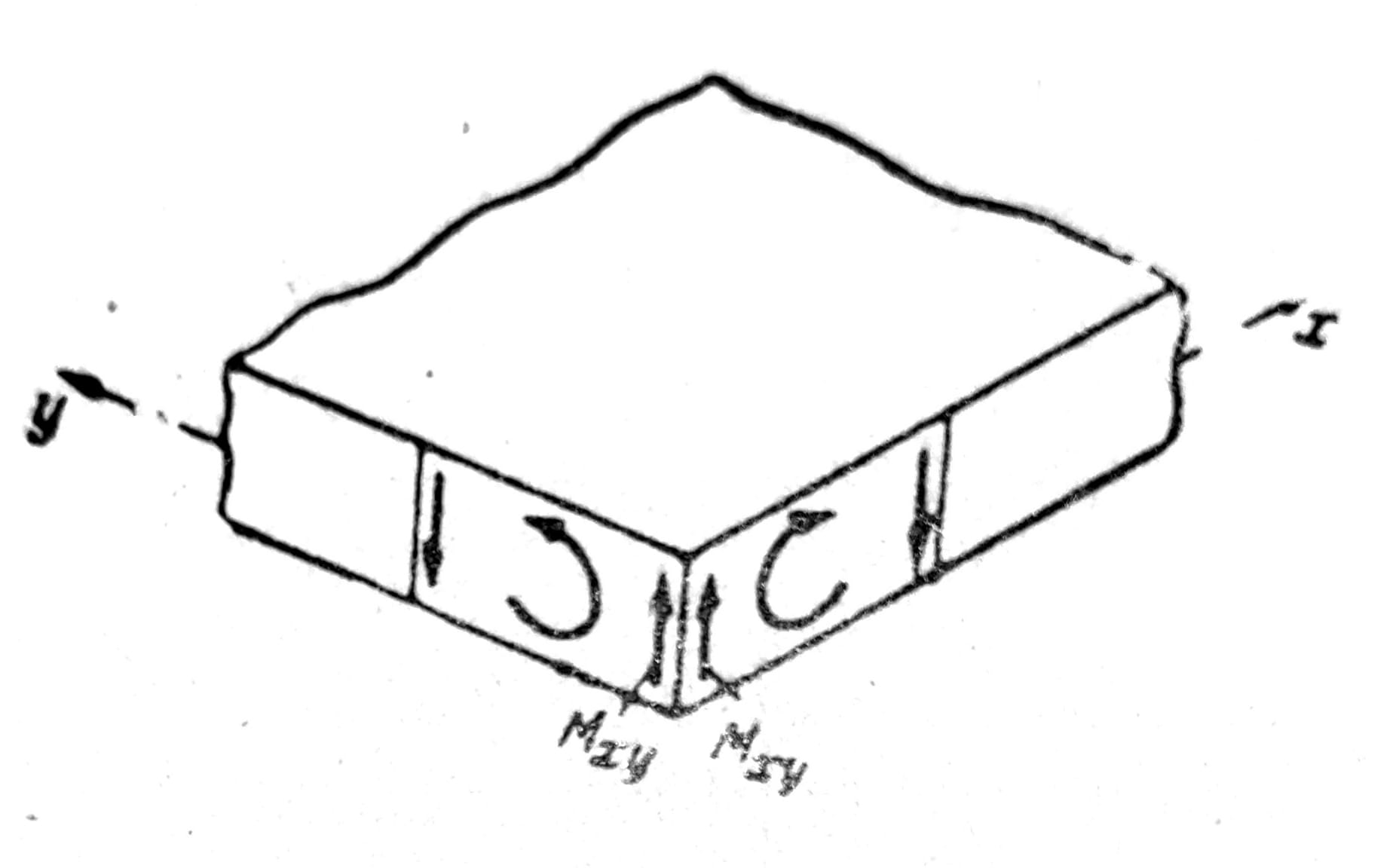
Na sl. 1 prikazan je element ploče. Naponi σ_x, σ_y τ_xy koji deluju u njegovvim vertikalnim stranama dx*t i dy*t mogu se, kao i naponi kod štapa izloženog savijanju i torziji, redukovati na momente:

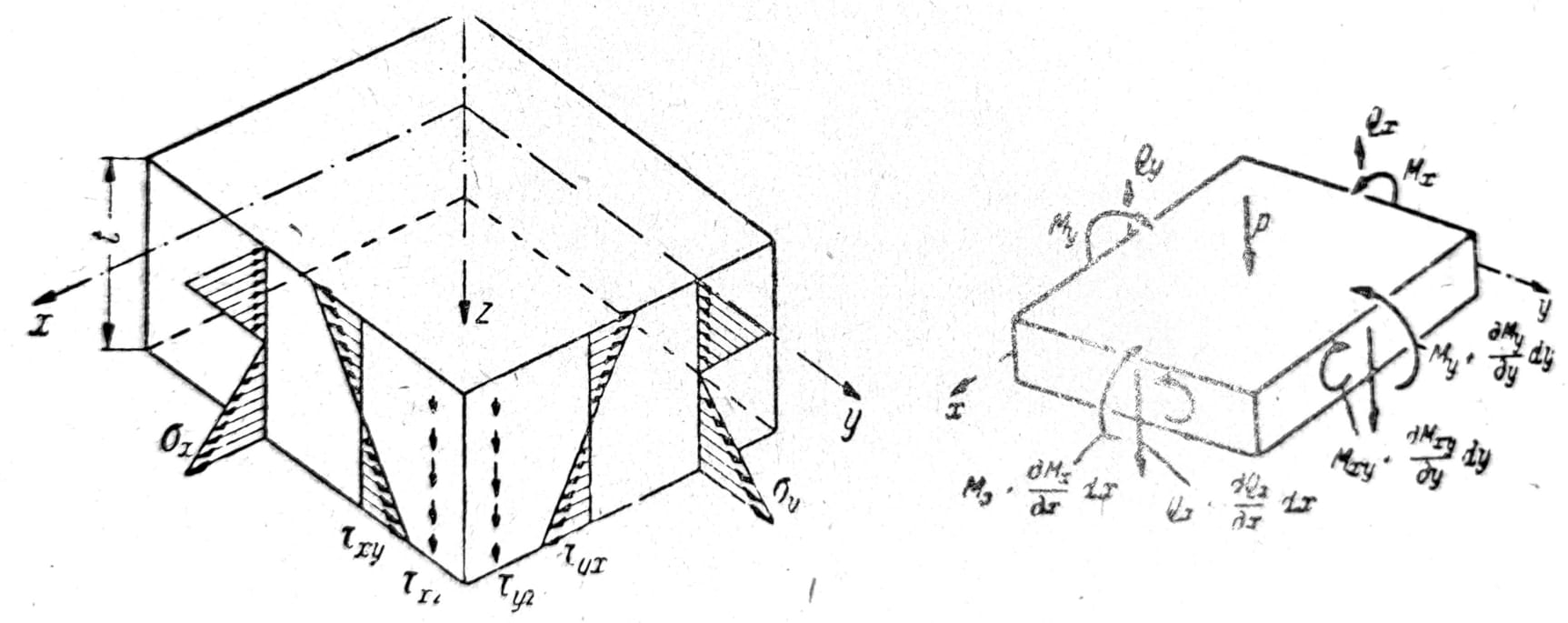
Sl. 1 i 2

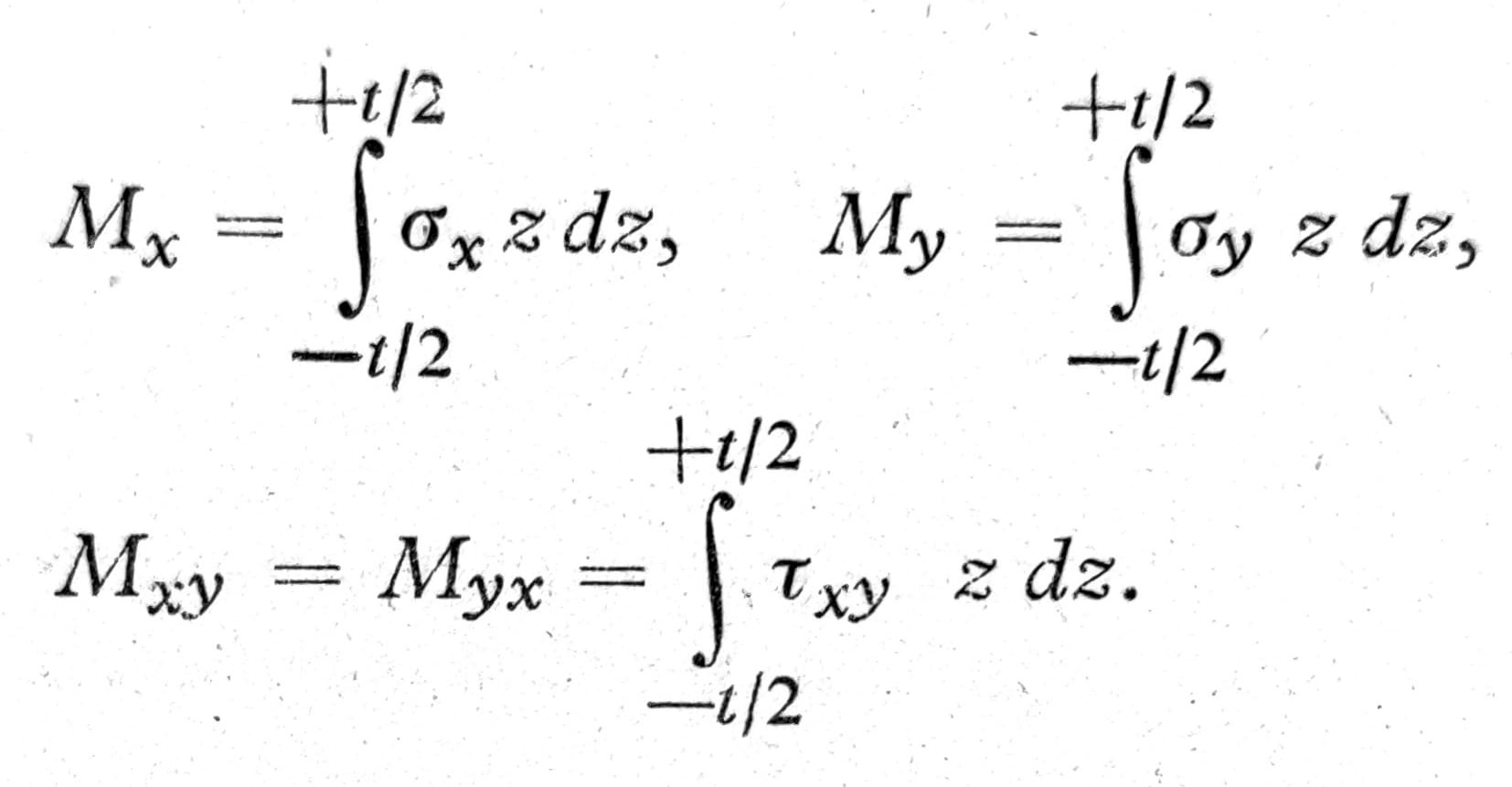
M_x i M_y se nazivaju momenti savijanja, a M_xy torzioni moment. Ovo su momenti na jedinicu dužine preseka x=const. ili y=const. pa imaju dimenziju moment po jedinici dužine.

Vertikalni smičući naponi τ_xz, τ_yz se slično tome redukuju na transverzalne sile

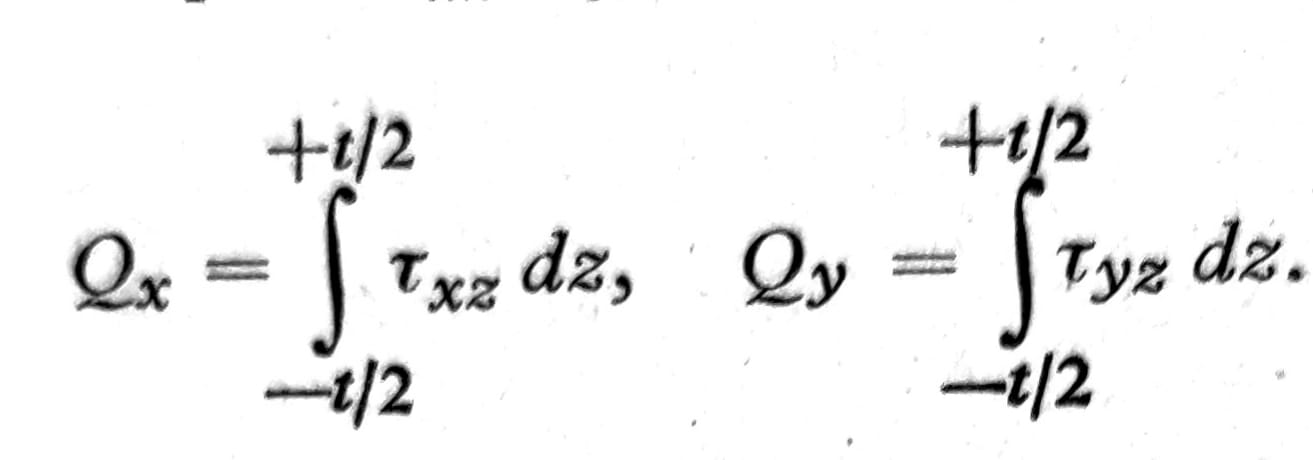
Veza između ovih presečnig sila i spoljašnjeg opterećenja p dx dy dobija se iz uslova ravnoteže (sl. 2):

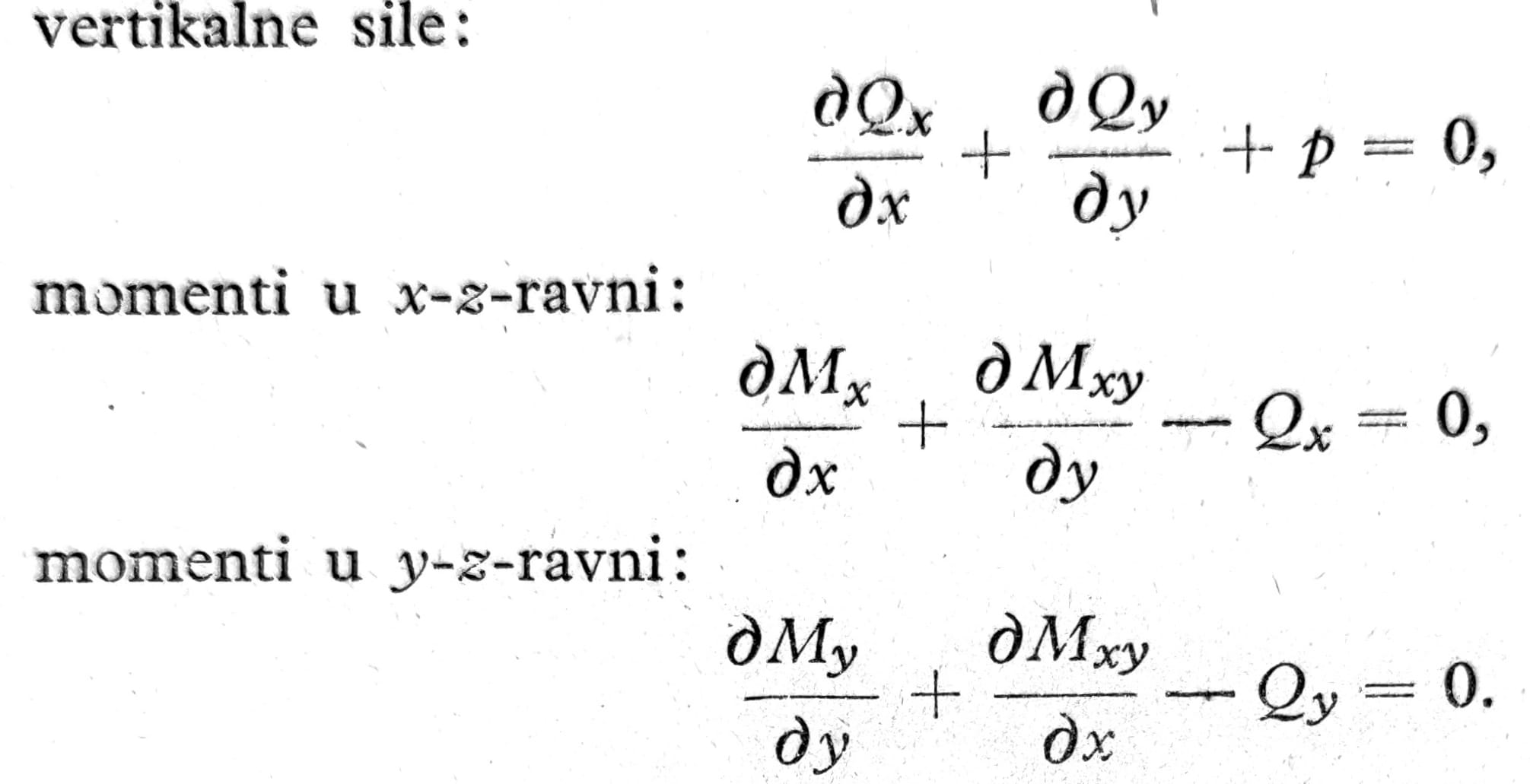
Na osnovu gore navedenih jednačina mogu se u prvoj jednačini transverzalne sile izraziti preko momenata savijanja i torzionog momenta:

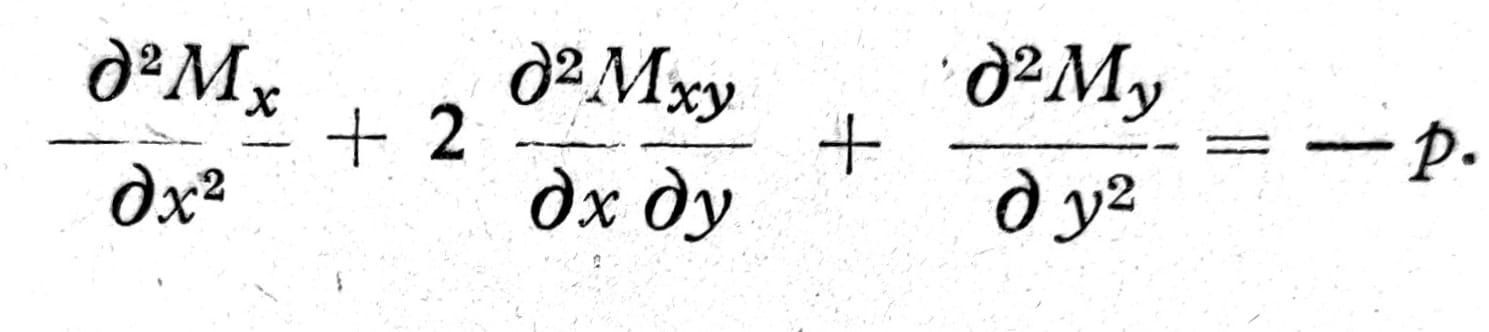
Deformacija ploče

Tri uslova ravnoteže nisu dovoljna za određivanje tri momenta i dve transverzalne sile. Zbog toga je potrebno da se prouči i deformacija ploče. Neka su u, v, w pomeranja tačke u pravcu koordinatnih osa x, y, z. Po analogiji sa teorijom savijanja štapova, o ovim pomeranjima se uvode sledeće pretpostavke, koje se zasnivaju na činjenici da je debljina ploče mala u poređenju sa ostale dve dimeznije:

1. Dilatacija ploče upravna na srednju ravan može se zanemariti. Prema tome w je nezavisno od z.

2. Prave upravne na srednju ravan prilikom deformacije ostaju prave i upravne na srednju površinu savijene ploče („elastična površina“).

3. Normalni napon σ_z u pravcu debljine ploče se može zanemariti.

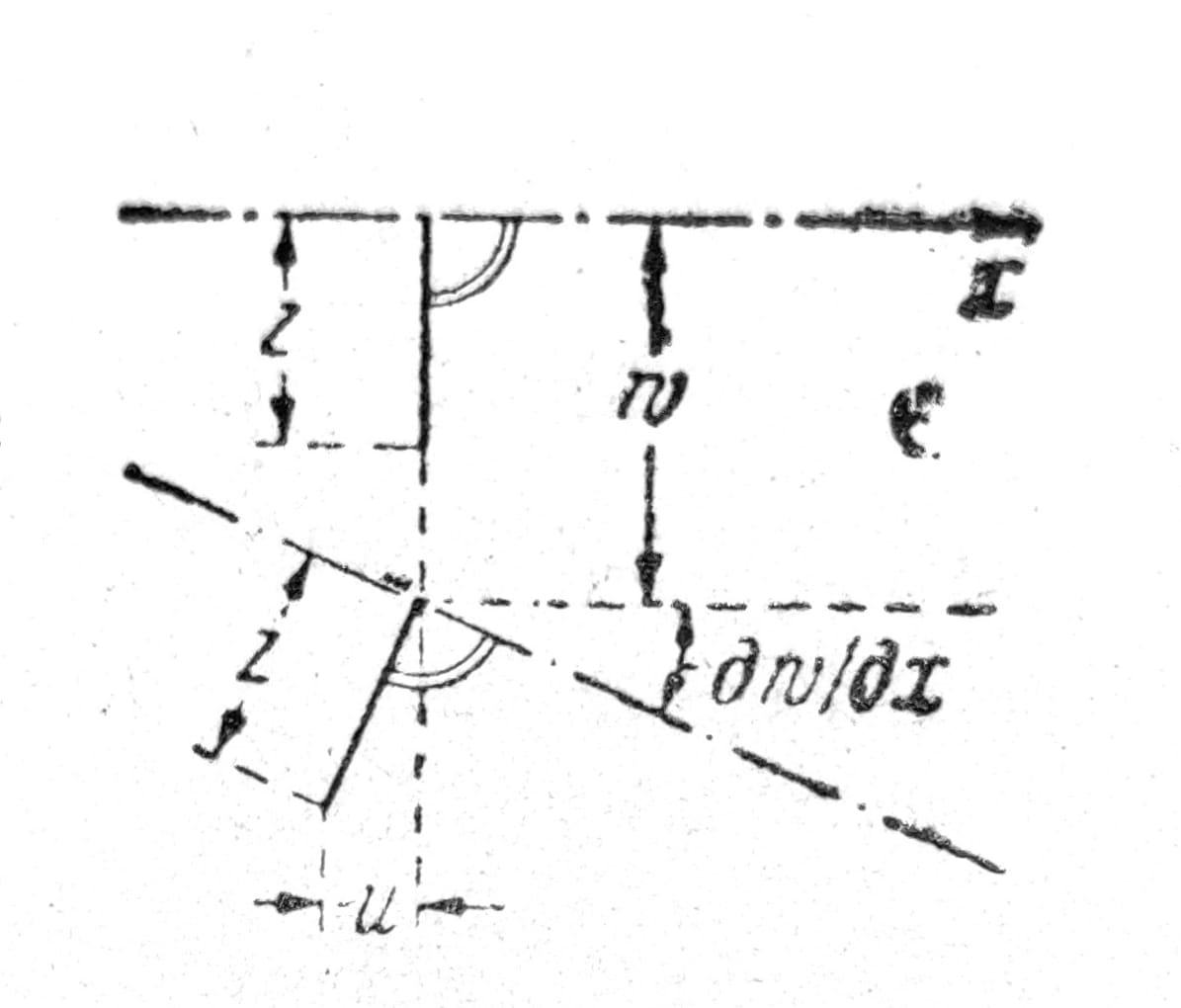
Sl. 3

Iz ovih pretopostavki na osnovu sl. 3 sledi:

u = -z dw/dy,   v = -z dq/dx

odakle se dobiju izrazi za komponentalne deformacije

ε_x = du/dx = -z d²w/dx²,   ε_y = dv/dy = -z d²w/dy²,   γ_xy = du/dy + dv/dx = -2z d²w/dxdy

pa se, uvođenjem Hooke-ovog zakona dobijaju sledeći naponi:

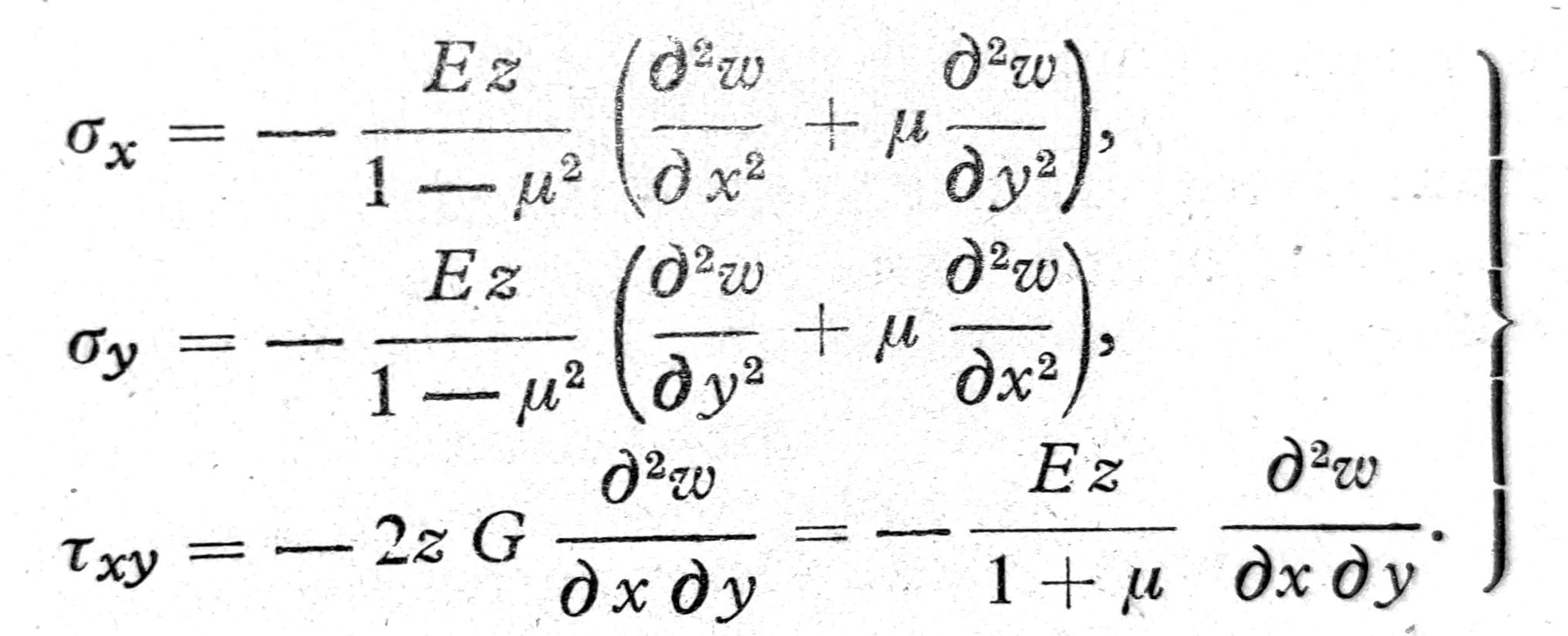
Jedn. 1

Kao što se vidi iz ovih jednačina, naponi usled momenata savijanja i torzionih momenata linearno su raspoređeni po debljini ploče i u srednjoj ravni su jednaki nuli. Prema tome, kada su poznati momenti savijanja i torzioni momenti, moguće ih je sračinati slično kao i napone usled savijanja u štapu pravougaonog poprečnog preseka.

Diferencijalna jednačina

Kada se naponi na osnovu jednačina iznad uvedu u jednačine 1 kojima su definisani momenti, može se sprovesti integraljenje po z, pa se dobija:

M_x = -K(d²w/dx² + μ d²w/dy²)   

M_y = -K(d²w/dy² + μ d²w/dx²)   (*)

M_xy = -K(1-μ) d²w/dxdy   

Veličina K naziva se krutost ploče. Ona predstavlja veličinu analognu krutosti EI grede. K=Et³/12(1-μ²). Kada se ovakve jednačine za momente uvedu u uslove ravnoteže, dobijaju se odgovarajući izrazi za transverzalne sile:

Q_x = -K d/dx (d²w/dx² + d²w/dy²)

Q_y = -K d/dy (d²w/dx² + d²w/dy²)

Ako se prethodno napisane momentne jednačine uvedu u uslov ravnoteže (4), dobija se diferencijalna jednačina za w, koja je osnovna diferencijalna jednačina savijanja ploča:

ΔΔw = d⁴w/dx⁴ + 2 d⁴w/dx²dy² + d⁴w/dy⁴ = p/K.

Granični uslovi

U pogledu graničnih uslova u obzir dolaze sledeći osnovni slučajevi:

a) Uklještena ivica. Ugib i nagib elastične površine u pravcu upravnom na ivicu su nula, prema tome je npr. za ivicu x=const. (tj. paralelno sa osovinom) w=0, dw/dx=0.

b) Slobodno oslonjena ivica. Osim ugiba ovde je moment savijanja nula, pa je za ivicu x=const. w=0, M_x=0. Osim transverzalne sile i torzioni moment M_xy je različit od nule, te oslonac mora da ga primi. Kako se ovo događa, pokazano je na sl. 4, gde se vidi deo ivice x=const. na kome su označena dva podužna elementa dy. Na njih napadaju torzioni momenti prikazani na sl. 4a. Ako se svaki od njih zameni spregom sila kraka dy, sile na levom elementu jednake su M_xy, a na desnom su veće za diferencijal. Kada se potiru odgovarajuće sile koje deluju na granici između oba elementa, pojavljuje se opterećenje (dM_xy/dy)dx. Podeljeno po dužini dy ono predstavlja dopunsku transverzalnu silu na ivici. Prema tome se, usled dejstva transverzalnih sila Q_x i torzionih momenata M_xy na ivici ploče, na jedinicu dužine oslonca prenosi vertikalno opterećenje veličine V_x = Q_x + dM_xy/dy. Dakle, reakcija oslonca V_x nije jednaka vrednosti transverzalne sile na ivici ploče, nego sadrži još jedan deo, Kirchhoff-ovu dopunsku transverzalnu silu.

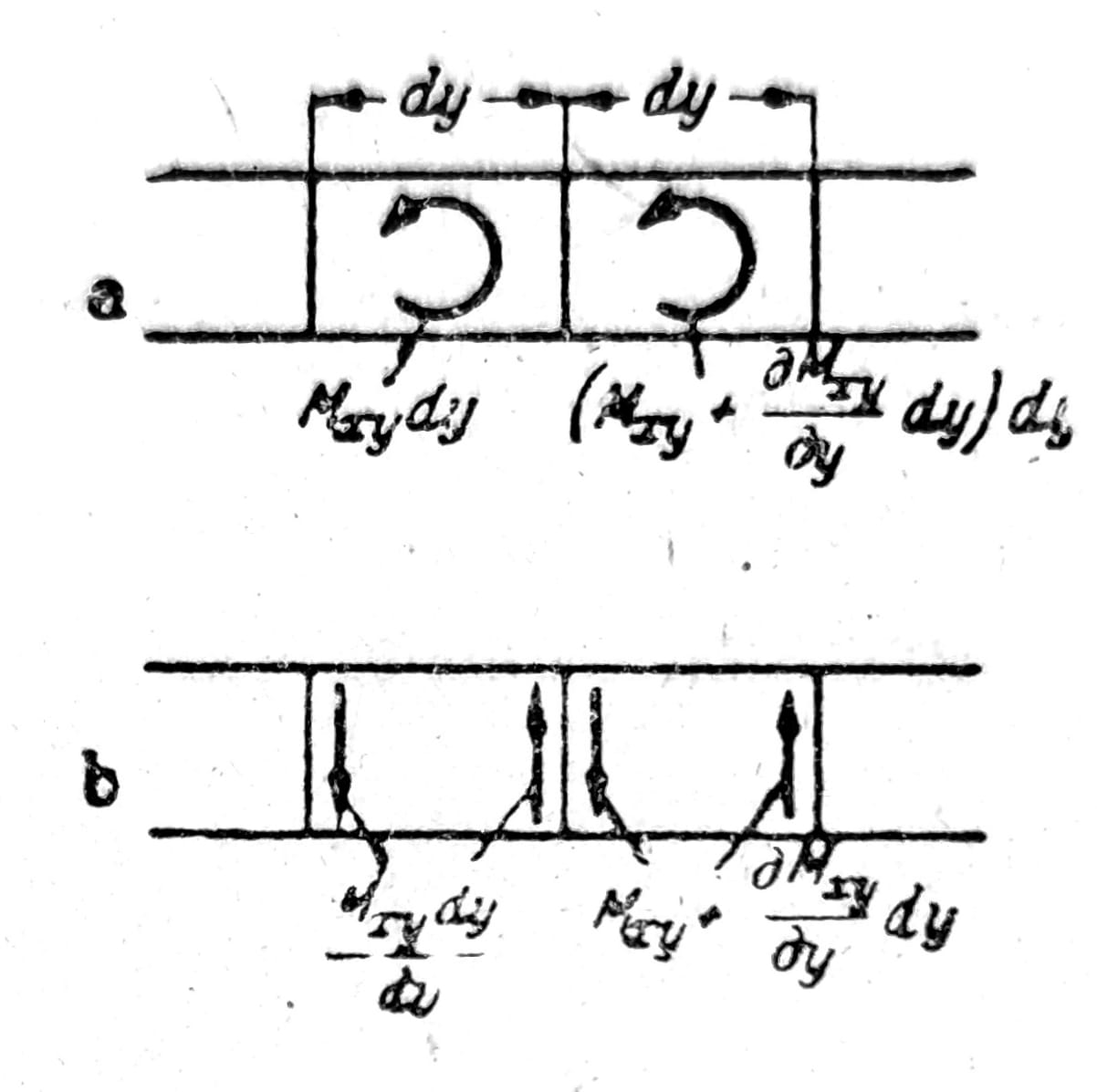
Sl. 4

Na uglu ploče (sl. 5) sile M_xy, prikazane na sl. 4b, ne potiru se tako da ostaje samo diferencijaln kao u prethodnom slučaju. Naprotiv, na osnovu stava o konjugovanosti smičućih napona, torzioni momenti na obe ivice koje se ovde sutiču imaju međusobno suprotan smer obrtanja, tako da se dopunske sile M_xy sabiraju i daju koncentrisanu silu veličine 2M_xy. Ovakve koncentrisane sile se uvek pojavljuju na uglovima pravougaonih slobodno oslonjenih ploča i da se one prihvate treba preduzeti posebne konstruktivne mere.

Sl. 5

c) Slobodna ivica. Ako neka ivica ploče nije oslonjena, moment savijanja i reakcija oslonca duž nje moraju da budu nula, tako da je npr. za ivicu x=const. M_x=0, V_x=0.

 

Kružne ploče

Kružna ploča konstantne debljine

Diferencijalna jednačina savijanja ploče u polarnim koordinatama glasi:

ΔΔw = (d²/dr² + 1/r d/dr + 1/r² d²/dφ²)² w = p/K.

Ako su opterećenje i način oslanjanja aksijalno simetrični, izvod po φ otpada. U ovom slučaju opšte rešenje glasi:

w=w₀(r) + C₁ + C₂r² + C₃ lnr + C₄ r² lnr.

Pri tome je w₀(r) rešenje nehomogene jednačine, npr. za p=const.:

w₀(r)=pr⁴/64K

ili za p=p₀r/a:

w₀(r)=p₀ r⁵/225Ka

Integracione konstante C₁ i C₄ određuju se iz graničnih uslova. Konstana C₃ je samo kod prstenastih ploča različita od nule, a C₄ i onda kada u središtu pune ploče deluje koncentrisana sila P, u kome slučaju ima vrednost C₄=P/8πK.

Za presečne sile u slučaju aksijalne simetrije dobijaju se transformacijom diferencijalnih jednačina sledeći obrasci (jedn. 2):

M_r = -K(d²w/dr² + μ/r dw/dr)

M_φ = -K(μ d²w/dr² + 1/r dw/dr)

Q_r = -K d/dr (d²w/dr² + 1/r dw/dr)

Gotovi obrasci za ugibe i presečne sile za neke najvažnije slučajeve opterećenja pune ploče uklještene na ivičnoj konturi r=a glase:

Superpozicijom se iz ovih obrazaca mogu dobiti rešenja za druge slučajeve opterećenja. Iz poslednjeg navedenog slučaja opterećenja diferenciranjempo b uz granični prelaz p db → P može se dobiti rešenje za slučaj linijskog opterećenja P na krugu r=b.

Obrasci za ploču slobodno oslonjenu duž ivice r=a dobijaju se superpozicijom navedenih obrazaca sa obrascima za slobodnu ploču opterećenu duž ivice momentima M_r = M

Ako se kod slobodno oslonjene ploče doda još linijsko opterećenje P odgovarajuće veličine na krugu r=b, dobijaju se obrasci za ploču koja je duž r=b slobodno oslonjena, a duž r=a ima slobodnu ivicu.

Ako su svi tereti proporcionalni odstojanju od prečnika φ=π/2, opšte rešenje glasi:

w(r, φ )=[ w₀(r) + C₁r³ + C₂r + C₃r lnr + C₄^r-1 ] cos φ.

Partikularno rešenje w₀(r) cosφ npr. za opterećenje p = p₀ x/a = p₀ r/a cosφ, koje se zajedno sa konstantnim opterećenjem može superponirati tako da se dobija hidrostatičko opterećenje, glasi:

w₀(r) cosφ = p₀ r⁵/192Ka cosφ.

Kružna ploča promenljive debljine

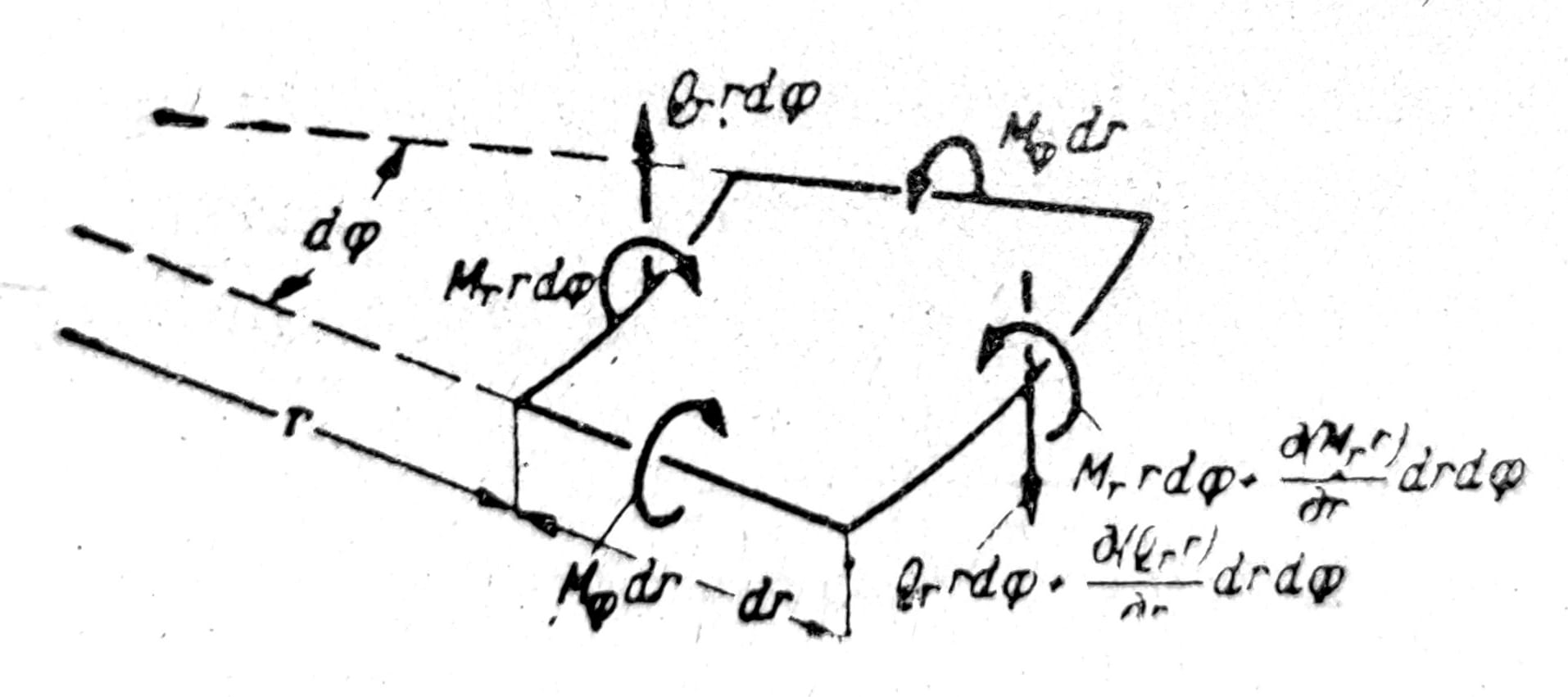
Sl. 6

Od obrazaca navedenih u prethodnom tekstu važe i za kružnu ploču promenljive debljine: uslovi ravnoteže i veze između momenata i ugiba. Uslovi ravnoteže u polarnim koordinatama pod pretpostavkom da je raspored napona aksijalno simetričan (sl. 6) glase:

vertikalne sile: d/dr (rQ_r)=-pr,

momenti u meridijalnoj ravni: d/dr(rM_r) - M_φ = rQ_r.

Ako se na osnovu jedn. 2 u uslovu ravnoteže momenata oba momenta savijanja izraze preko w, dobija se, označavajući izvode po r crticama:

rQ_r = -K(rw’’+w’-w’/r) – K(rw’’+μw’),

pa iz ravnoteže vertikalnih sila odavde sledi diferencijalna jednačina:

K(rw’’+w’’-w’/r) + K(rw’’+μw’)=∫prdr + C.

Ova jednačina se može još uprostiti ako se kao nepoznata uvede nagib elastične površine ψ=w’:

ψ’’+(1/r + K’/K)ψ’ – 1/r(1/r-μ K’/K)ψ = 1/Kr [∫prdr + C].

 

Pravougaone ploče

Rešenje u obliku reda

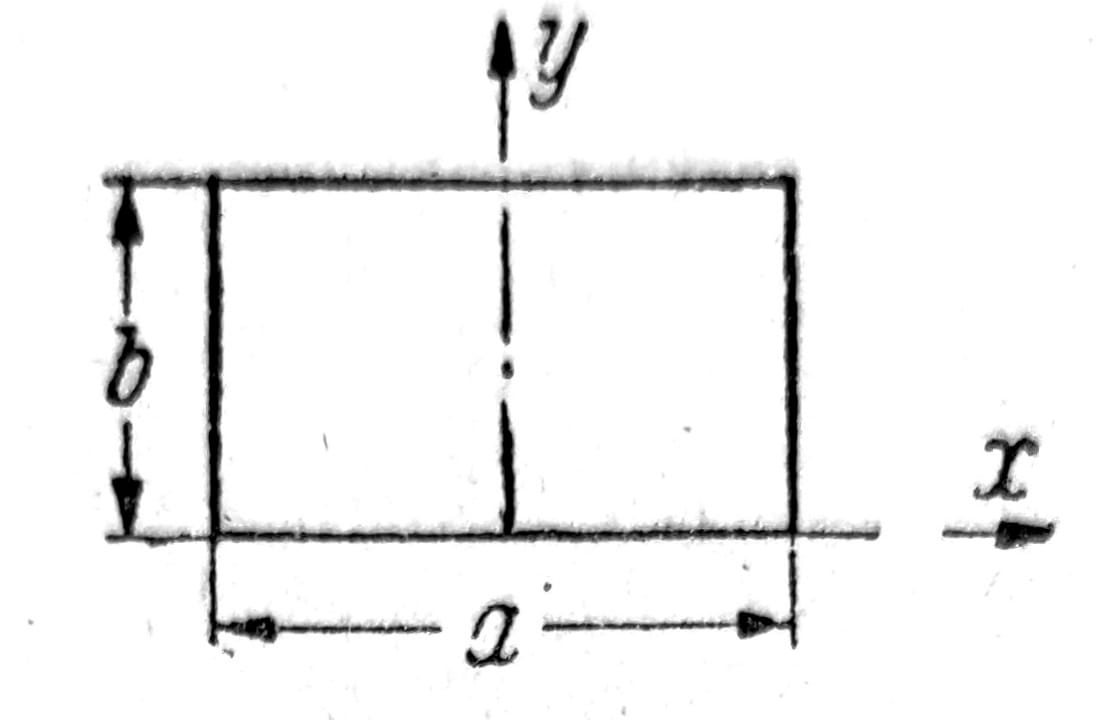
Sl. 7

U mnogim slučajevima može se lako odrediti partikularno rešenje koje zadovoljava granične uslove na dve naspramne ivice. Ako je, npr. pravougaona ploča (sl. 7) opterećena jednakopodeljenim opterećenjem i slobodno odlonjena duž ivica y=0, y=b, tada je:

w = w₀ = p/24K (y⁴ – 2by³ + b³y)

jedno takvo partikularno rešenje. Ono, doduše, na ivicama x=±a/2 zadovoljava uslov uklještenja dw/dx = 0, ali su na tom mestu i ugib w i moment M_X različiti od nule. Da bi ovde bili zadovoljeni granični uslovi koji imaju fizičkog slisla, mora se superponirati pogodno rešenje homogene jednačine ΔΔw=0, koje ne narušava već zadovoljene uslove na drugim dvema ivicama. Ovakvo rešenje:

w=∑x_n(x) sin nπy/b  (3)

gde je

X_n=(A_n+B_nx) e^nπx/b + (C_n+D_nx) e^-nπx/b

Da bi se integracione konstante stvarno odredile moraju se vrednosti w₀ na ivici ploče koje ne zadovoljavaju granične uslove razviti u Fourier-ov red, pa se dobija

w₀=4pb⁴/Kπ⁵ ∑1/n⁵ sin nπy/b.

Iz graničnog uslova da su zbir w₀ i w₁ iz jedn. (3) vrednosti w i M_x na ivici ploče nula, dobijaju se za svako n dve jednačine po A’_n i D’_n, odakle sledi rešenje:

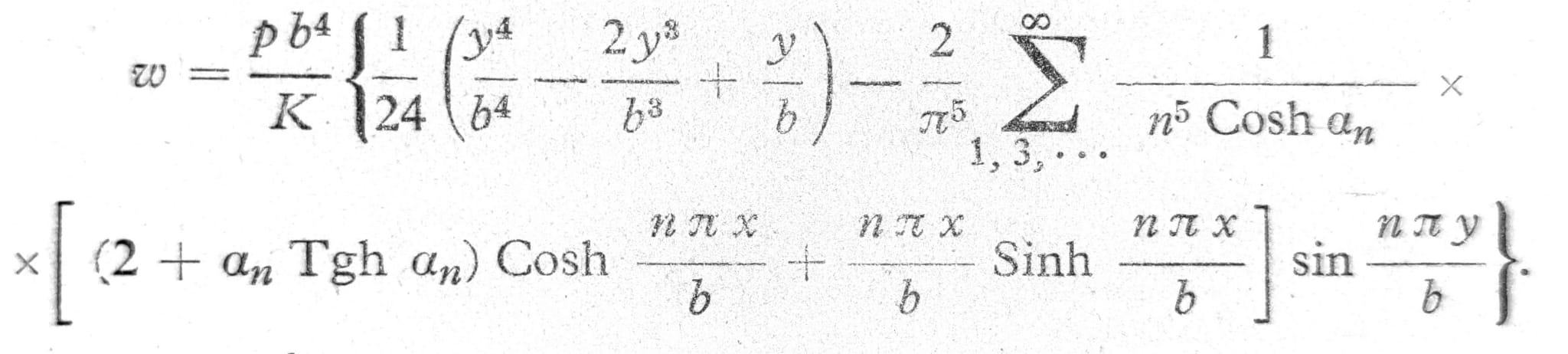
Ovde, kao i u svim sledećim obrascima, je a_n=nπa/2b. Kada su poznati ugibi w lako je diferenciranjem izvesti obrasce za momente savijanja, torzione momente i transverzalne sile. Nije preporučljivo da se u ovim obrascima algebarski deo izrazi u obliku Fouriev-ovog reda, jer se time konvergencija redova osetno pogoršava.

Ovaj metod rešenja može se primeniti za proizvoljne granične uslove duž ivica x=const. i za opterećenja čiji intenzitet zavisi od y, ali ne i od x; ali je po suštini stvari uslovljen pretpostavkom da su ivice y=const. slobodno oslonjene. U daljem su navedena još neka rešenja (oznake prema sl. 7).

Izraz za y≥b/2 je na odgovarajući način simetričan.

U mnogim slučajevima, a posebno kada su granični uslovi duž ivica x=±a/2 međusobno različiti, opšti obrasci postaju i suviše složeni, pa je tada bolje da se što ranije uvedu brojne vrednosti za pojedine slučajeve opterećenja. Kod ovakvih problema korisno je da se raspolaže gotovim obrascima za ivično opterećenje, kao što su npr. sledeći koji se odnose na simetrične slučajeve:

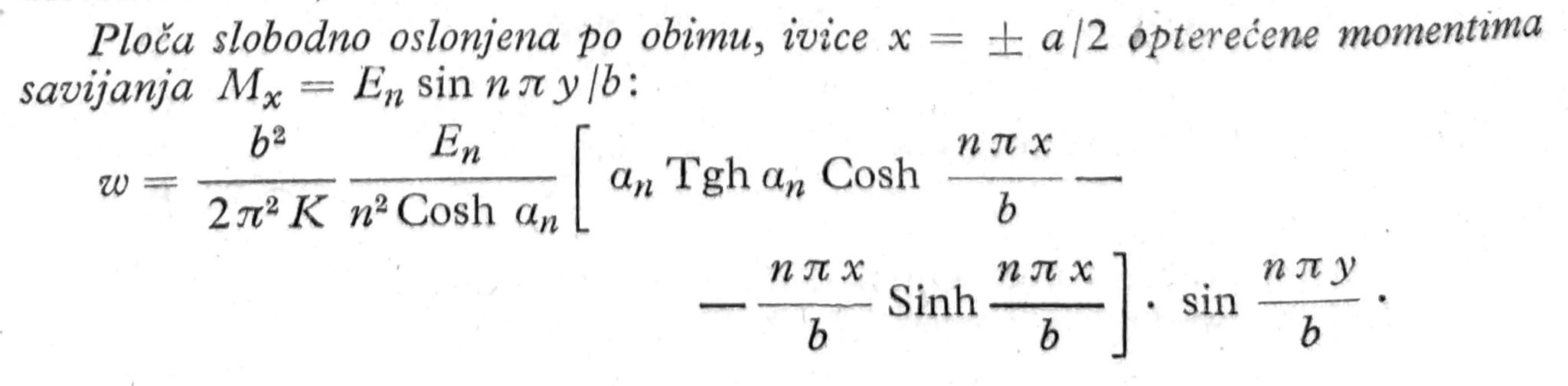
Nije neophodno da partikularno rešenje koje se u računu koristi predstavlja ugibe proste grede. Kod ploče sa koncentrisanim teretom P na sredini polazi se od rešenja

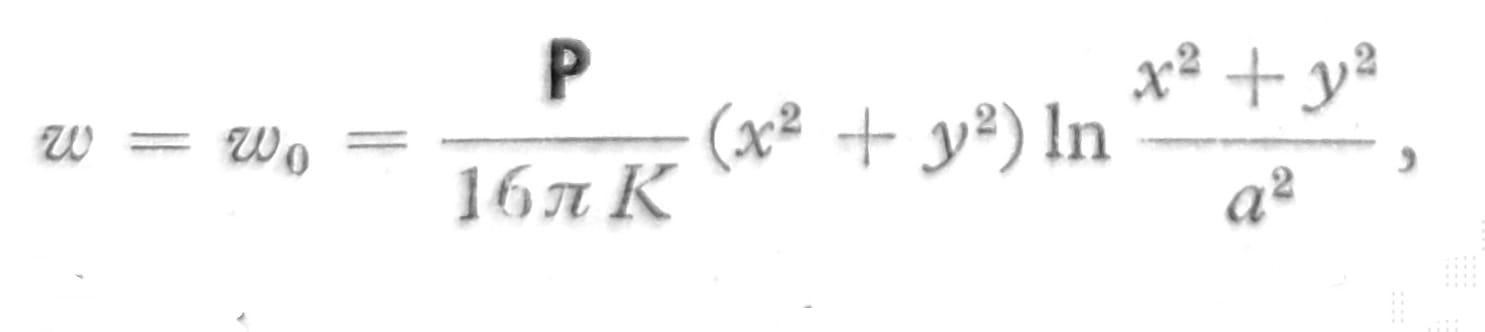
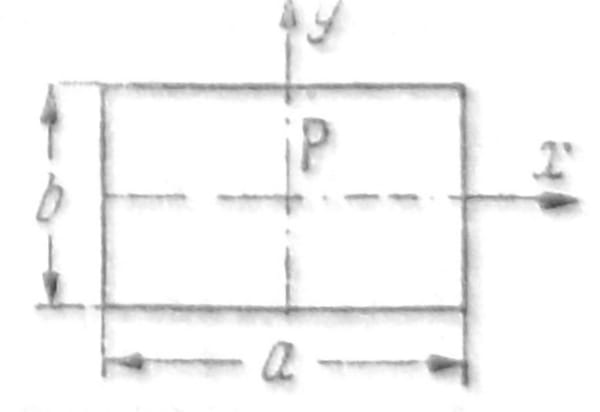
koje dobro prikazuje singularno ponašanje u okolini napadne tačke tereta, zatim se određuju odgovarajuće vrednosti ugiba i momenta savijanja na ivicama, koje se onda mogu numerički razviti u Fourier-ov red. Pomoću rešenja i jedn. iznad, može se postići da ugib w i moment M_x na ivicama x=±a/2 bude nula. Da bi se zadovoljili uslovi i na druge dve ivice, u jednačinama iznad treba međusobno zameniti x i y, a i b. Na sl. 8 dati su neki brojni podaci. Treba uočiti da u ovom slučaju veličina momenata savijanja i torzionog momenta ne zavisi od raspona ploče.

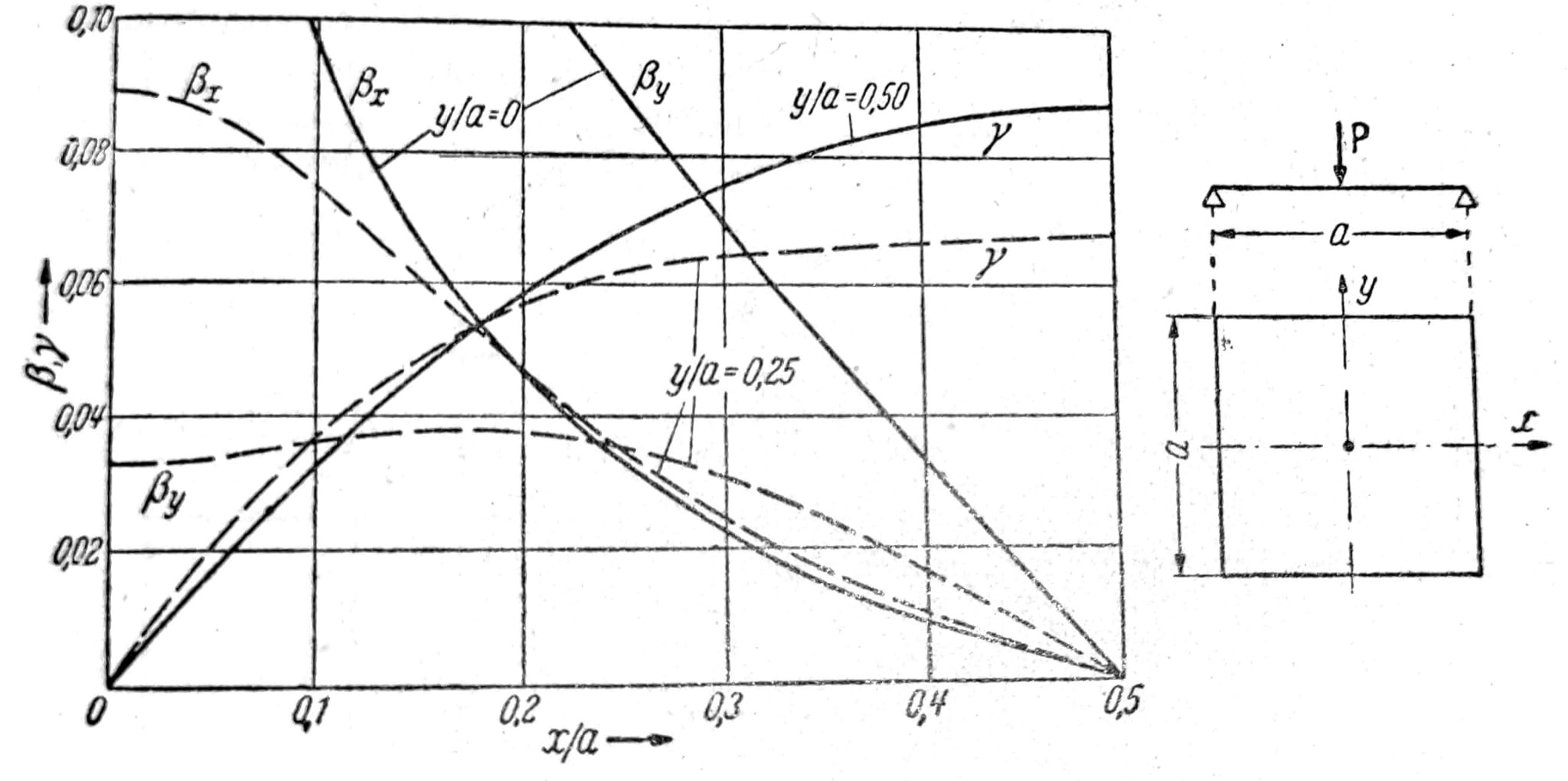
Sl. 8 - Momenti u slobodno oslonjenoj ploči opterećenoj konc. teretom

U svim ovim obrascima je konvergencija Fourier-ovih redova utoliko bolja ukoliko je veći odnos strana a/b. Kada je a/b>4, srednji deo ploče se ponaša kao skup greda položenih jedna pokraj druge, no s tim da se ovde osim momenata M_y pojavljuju i momenti M_x=μM_y, v. jednačine (*).

Na krajevima duge ploče javlja se poremećaj, koji je nezavisan od dužine a. Tako je, npr. na kraju vrlo duge ploče pod jednakopodeljenim opterećenjem p (sl. 9):

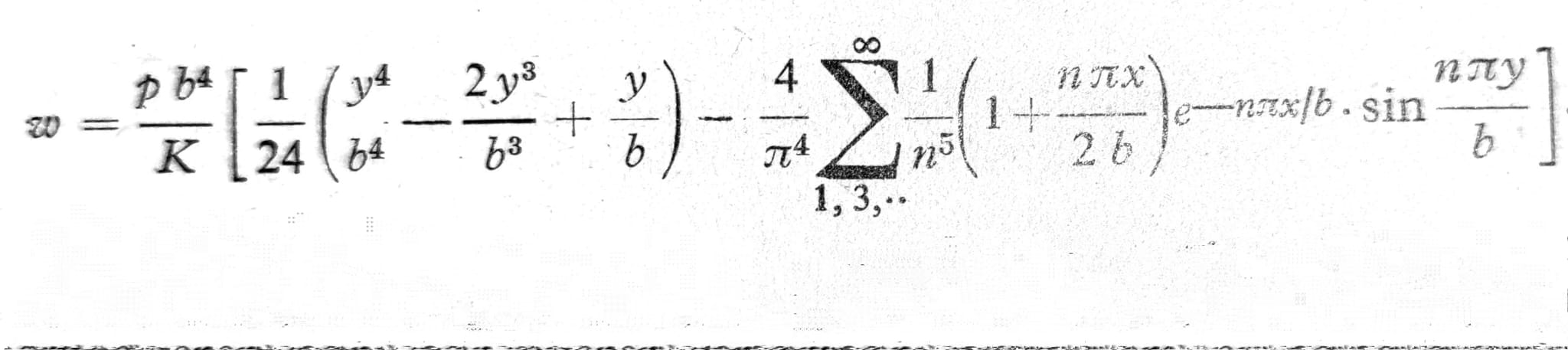
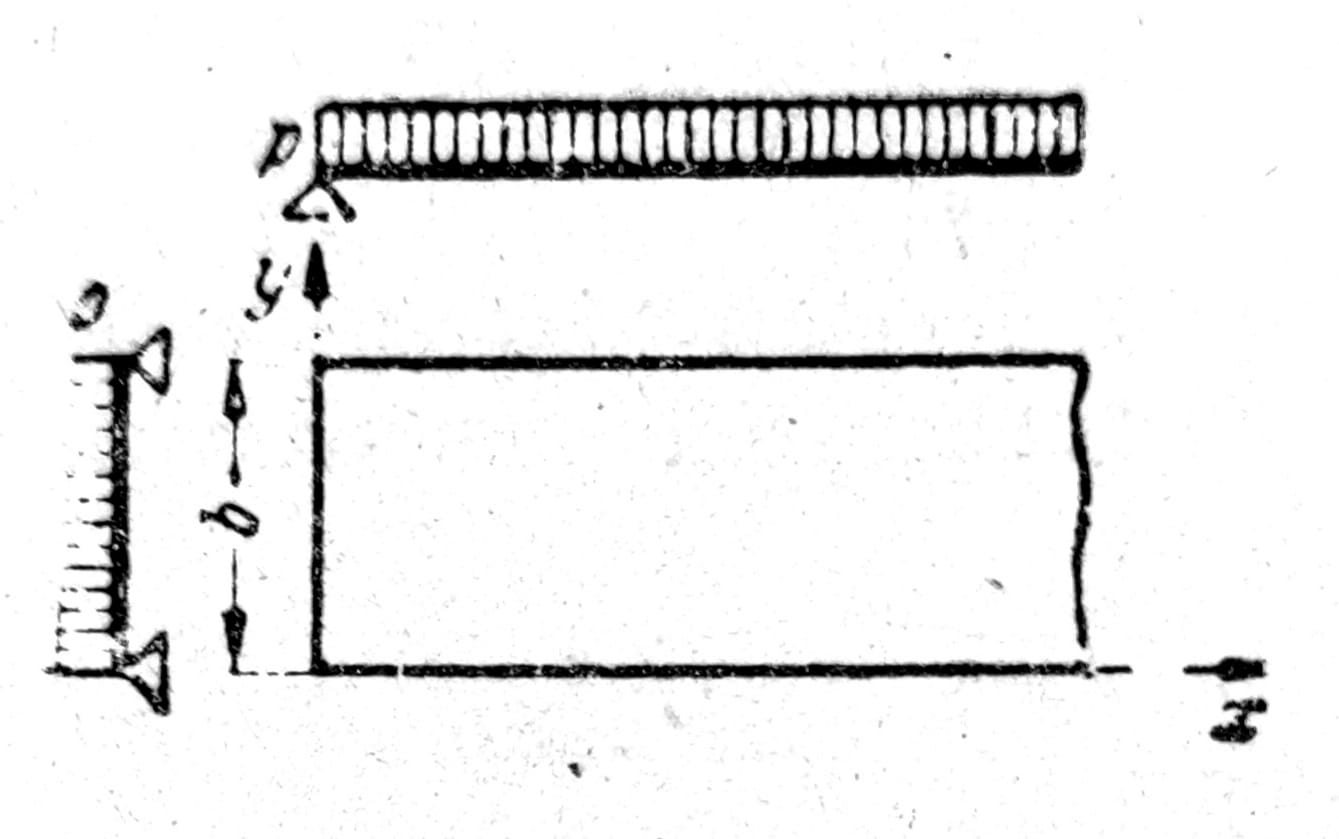
Sl. 9

Da bi se rešio slučaj prikazan na sl. 10, gde linijsko opterećenje intenziteta P (sila na jedinicu dužine) deluje, duž raspona b, dovoljno je da se primeni homogeno rešenje (3). Raspored napona je simetričan u odnosu na y-osovinu. Za desnu stranu x≥0 je:

w=Pb²/Kπ⁴ ∑1/n⁴ (1+nπx/b) e^-nπx/b sin nπy/b.

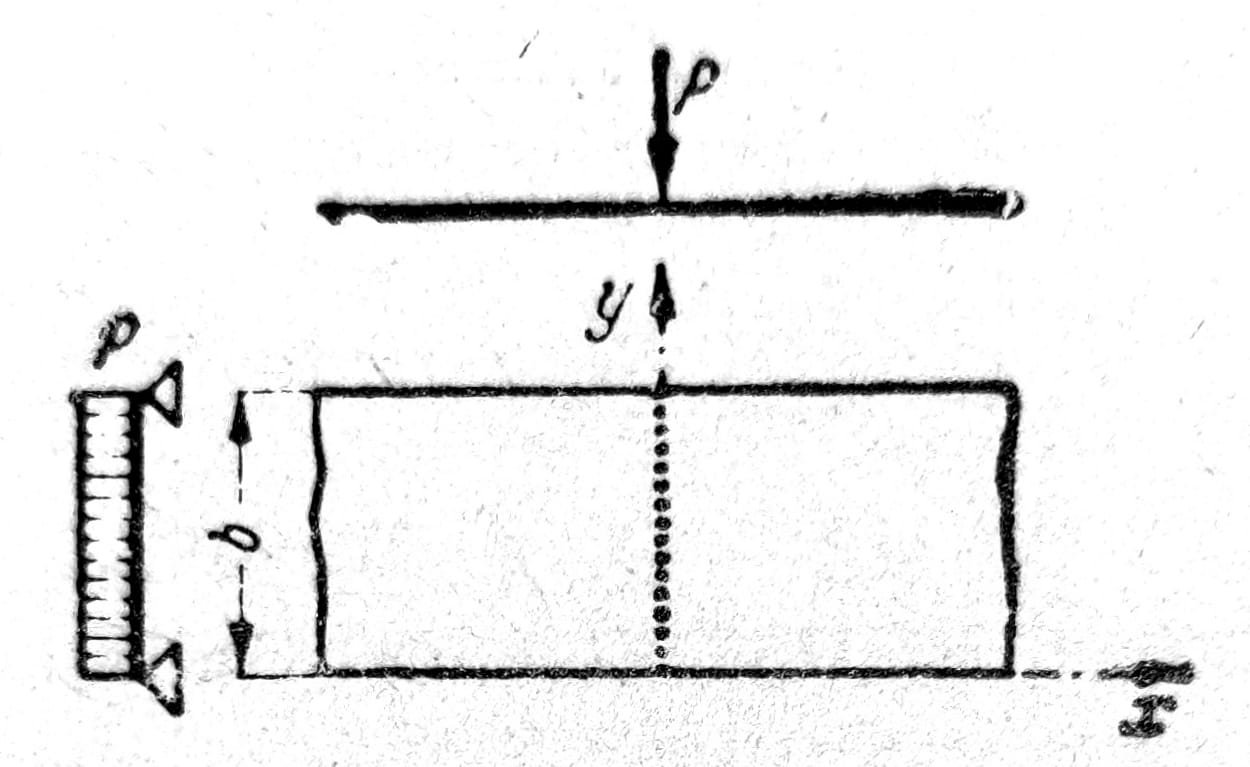
Sl. 10